-
Câu hỏi:
Cho đường tròn (O;15), Dây AB không đi qua tâm. Qua O vẽ đường thẳng vuông góc với AB cắt tiếp tuyến tại A ở C và cắt AB ở D.Biết AB=24. Độ dài OC là:
- A. 12
- B. 19
- C. 25
- D. 32
Lời giải tham khảo:
Đáp án đúng: C
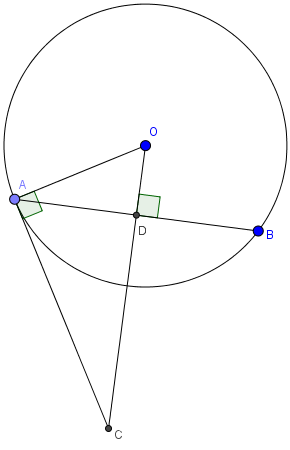
Xét tam giác vuông OAD: Áp dụng định lý pi-ta-go ta có: \(OD=\sqrt{OA^2-AD^2}=\sqrt{R^2-\frac{AB^2}{4}}=9\)
Vì tam giác OAC vuông tại A và có AD là đường cao nên: \(OA^2=OD.OC\Rightarrow OC=\frac{OA^2}{OD}=\frac{15^2}{9}=25\)
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
YOMEDIA
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Cho tam giác ABC có AH là đường cao ( H thuộc BC). Đường tròn (A;AH) sẽ có vị trí như thế nào với các cạnh của tam giác ABC
- Trong các phát biếu dưới đây phát biểu nào đúng
- Cho đường tròn (O;15), Dây AB không đi qua tâm. Qua O vẽ đường thẳng vuông góc với AB cắt tiếp tuyến tại A ở C và cắt AB ở D.Biết AB=24. Độ dài OC là:
- Cho đường tròn (O). A, B, C là 3 điểm thuộc đường tròn sao cho tam giác ABC cân tại A.Phát biểu nào sau đây đúng. Tiếp tuyến của đường tròn tại A là
- Cho tam giác ABC có AB=3, AC=4, BC=5. Khi đó:
