Câu hỏi trắc nghiệm (45 câu):
-
Câu 1: Mã câu hỏi: 48727
Tiếp tuyến của đồ thị hàm số \(y = \ln x\) tại điểm có hoành độ \(x = {e^2}\) là:
- A. \(y = \frac{1}{{{e^2}}}x + 1.\)
- B. \(y = \frac{1}{{{e^2}}}x - 2.\)
- C. \(y = \frac{1}{{{e^2}}}x.\)
- D. \(y = \frac{1}{{{e^2}}}x - 1.\)
-
Câu 2: Mã câu hỏi: 48728
Tất cả các giá trị của \(m\) để hàm số \(y = - {x^3} - 3{x^2} + mx - 3\) nghịch biến trên \(R\) là:
- A. \(\left[ { - 3; + \infty } \right) \cdot \)
- B. \(( - 3; + \infty ) \cdot \)
- C. \(\left( { - \infty ; - 3} \right] \cdot \)
- D. \(\left( { - \infty ; - 3} \right) \cdot \)
-
Câu 3: Mã câu hỏi: 48729
Tìm tất cả các giá trị của tham số \(m\) để hàm số \(y = \frac{{mx + 4}}{{x + m}}\) nghịch biến trên khoảng \(\left( {1; + \infty } \right)\)?
- A. \( - 2 \le m \le 2.\)
- B. \( - 1 \le m < 2.\)
- C. \( - 1 \le m \le 2.\)
- D. \( - 2 < m < 2.\)
-
Câu 4: Mã câu hỏi: 48730
Thể tích của khối lập phương có cạnh \(3a\) là:
- A. \(27{a^3} \cdot \)
- B. \({a^3} \cdot \)
- C. \(9{a^3} \cdot \)
- D. \(18{a^3} \cdot \)
-
Câu 5: Mã câu hỏi: 48731
Cho \(a > 0,b > 0\) thỏa mãn: \({a^{\frac{1}{2}}} < {a^{\frac{1}{3}}}\) và \({b^{\frac{2}{3}}} < {b^{\frac{3}{4}}}\). Khi đó:
- A. \(0 < a < 1,0 < b < 1.\)
- B. \(a > 1,0 < b < 1.\)
- C. \(0 < a < 1,b > 1.\)
- D. \(a > 1,b > 1.\)
-
Câu 6: Mã câu hỏi: 48732
Hàm số \(y = \frac{{x + 1}}{{x - 1}}\) đạt GTLN, GTNN trên đoạn \(\left[ { - 4; - 2} \right]\) theo thứ tự là:
- A. \(3;\frac{3}{5} \cdot \)
- B. \(\frac{3}{5};\frac{1}{3} \cdot \)
- C. \(3;\frac{1}{3} \cdot \)
- D. \(\frac{1}{3};\frac{3}{5} \cdot \)
-
Câu 7: Mã câu hỏi: 48733
Số mặt phẳng đối xứng của hình chóp tam giác đều?
- A. 0
- B. 3
- C. 1
- D. 2
-
Câu 8: Mã câu hỏi: 48734
Cho \(0 < a \ne 1\). Mệnh đề nào đúng trong các mệnh đề sau:
- A. \({\log _a}x\) có nghĩa với \(\forall x.\)
- B. \({\log _a}{x^n} = n{\log _a}x,(x > 0;n \ne 0).\)
- C. \({\log _a}a = 0;{\log _a}1 = 1.\)
- D. \({\log _a}xy = {\log _a}x.{\log _a}y.\)
-
Câu 9: Mã câu hỏi: 48735
Một hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông
bằng \(2a\). Diện tích toàn phần của hình nón là:
- A. \(2\sqrt 2 \pi {a^2}.\)
- B. \(4\pi {a^2}.\)
- C. \(2\pi {a^2}(\sqrt 2 + 1).\)
- D. \(2\pi {a^2}(2\sqrt 2 + 1).\)
-
Câu 10: Mã câu hỏi: 48736
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây là đúng:
.png)
- A. Hàm số đạt cực tiểu tại \(x=-1\).
- B. Hàm số nghịch biến trên khoảng \(( - \infty ; - 1)\) và \((1; + \infty ).\)
- C. Hàm số đồng biến trên khoảng \((-1;1)\)
- D. Hàm số đạt cực tiểu tại \(x=1\).
-
Câu 11: Mã câu hỏi: 48737
Tất cả các giá trị của \(m\) để hàm số \(y = (1 - m){x^4} - 2(m - 3){x^2} + 1\) không có cực tiểu?
- A. \(1 \le m \le 3.\)
- B. \(m \le 1.\)
- C. \(m \ge 3.\)
- D. \(1 < m \le 3.\)
-
Câu 12: Mã câu hỏi: 48738
Thể tích của khối cầu ngoại tiếp hình lập phương cạnh \(2a\) là:
- A. \(2\sqrt 3 \pi {a^3}.\)
- B. \(\sqrt 3 \pi {a^3}.\)
- C. \(4\pi {a^3}.\)
- D. \(4\sqrt 3 \pi {a^3}.\)
-
Câu 13: Mã câu hỏi: 48739
Tập xác định của hàm số \(y = {\log _3}\left| {1 - {x^2}} \right|\) là:
- A. \(R\backslash \left\{ { \pm 1} \right\}.\)
- B. \(R\backslash \left\{ { - 1} \right\}.\)
- C. \(R\)
- D. \(R\backslash \left\{ 1 \right\}\)
-
Câu 14: Mã câu hỏi: 48740
Hình chóp \(S. ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\), \(SA\) vuông góc với mặt phẳng đáy và \(SA = a\sqrt 3 \). Thể tích khối chóp \(S.ABC\) theo \(a\) là:
- A. \(\frac{{{a^3}}}{{12}} \cdot \)
- B. \(\frac{{{a^3}}}{{4}} \cdot \)
- C. \(\frac{{{3a^3}}}{{4}} \cdot \)
- D. \(\frac{{{a^3}}}{{2}} \cdot \)
-
Câu 15: Mã câu hỏi: 48741
Cho hàm số \(y = - x + 2 - \frac{2}{{x + 1}}\). Khi đó \(2{y_{CD}} + {y_{CT}}\) bằng:
- A. \(9 - 2\sqrt 2 .\)
- B. \(9 + 2\sqrt 2 .\)
- C. \(6\)
- D. \( - 2\sqrt 2 .\)
-
Câu 16: Mã câu hỏi: 48742
Cho lăng trụ \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác đều cạnh bằng \(a\). Hình chiếu vuông góc của \(A\) lên mặt phẳng \(A'B'C'\) là trung điểm cạnh \(A'B'\). Mặt bên \(AA'C'C\) tạo với đáy góc \({45^0}\). Thể tích khối lăng trụ \(ABC.A'B'C'\) là:
- A. \(\frac{{a{}^3}}{2} \cdot \)
- B. \(\frac{{3a{}^3}}{4} \cdot \)
- C. \(\frac{{3a{}^3}}{16} \cdot \)
- D. \(\frac{{3a{}^3}}{8} \cdot \)
-
Câu 17: Mã câu hỏi: 48743
Số giao điểm của đồ thị hàm số \(y = {x^3} - 3{x^2} + 4\) và đường thẳng \(y=4\) là:
- A. 2
- B. 0
- C. 3
- D. 1
-
Câu 18: Mã câu hỏi: 48744
Tổng các nghiệm của phương trình \({4^x} - {2^{x + 2}} + 3 = 0\) là:
- A. \(1 + {\log _2}3.\)
- B. \({\log _2}3.\)
- C. \(1\)
- D. \(1 - {\log _2}3.\)
-
Câu 19: Mã câu hỏi: 48745
Cho hàm số \(y = \frac{{\ln x}}{x}\). Mệnh đề nào đúng trong các mệnh đề sau:
- A. \(2y' + xy'' = \frac{{ - 1}}{{{x^2}}} \cdot \)
- B. \(y' + xy'' = \frac{1}{{{x^2}}} \cdot \)
- C. \(y' + xy'' = \frac{{ - 1}}{{{x^2}}} \cdot \)
- D. \(2y' + xy'' = \frac{1}{{{x^2}}} \cdot \)
-
Câu 20: Mã câu hỏi: 48746
Cho khối chóp \(S.ABC\). Lấy \(A', B'\) lần lượt thuộc \(SA. SB\) sao cho \(3SA' = AA'\), \(2SB'= BB'\). Tỷ số thể tích giữa hai khối chóp \(S.A'B'C\) và \(S.ABC\) là:
- A. \(\frac{1}{{12}} \cdot \)
- B. \(\frac{1}{{4}} \cdot \)
- C. \(12\)
- D. \(\frac{1}{{3}} \cdot \)
-
Câu 21: Mã câu hỏi: 48747
Bán kính mặt cầu ngoại tiếp lăng trụ tam giác đều có cạnh đáy bằng \(2a\), cạnh bên bằng \(a\) là:
- A. \(\frac{{a\sqrt {39} }}{6} \cdot \)
- B. \(\frac{{a\sqrt {57} }}{3} \cdot \)
- C. \(\frac{{a\sqrt {12} }}{6} \cdot \)
- D. \(\frac{{a\sqrt {57} }}{6} \cdot \)
-
Câu 22: Mã câu hỏi: 48748
Đồ thị hàm số nào sau đây có đúng một điểm cực trị?
- A. \(y = {x^4} - 2{x^2} - 1.\)
- B. \(y = 2{x^4} + 4{x^2} + 1.\)
- C. \(y = - {x^4} + {x^2} - 1.\)
- D. \(y = - {x^4} + 2{x^2} - 1.\)
-
Câu 23: Mã câu hỏi: 48749
Cho hàm số \(y = f(x) = - {x^3} + {x^2} - 3x - 1\). Chọn khẳng định đúng trong các khẳng định sau:
- A. Đồ thị hàm số \(y=f(x)\) cắt trục hoành tại đúng ba điểm phân biệt.
- B. Đồ thị hàm số \(y=f(x)\) không cắt trục hoành.
- C. Đồ thị hàm số \(y=f(x)\) cắt trục hoành tại đúng hai điểm phân biệt.
- D. Đồ thị hàm số \(y=f(x)\) cắt trục hoành tại đúng một điểm.
-
Câu 24: Mã câu hỏi: 48750
Lãi suất tiết kiệm là bao nhiêu một năm nếu bạn gửi vào ngân hàng 15,625 triệu đồng và sau ba năm rút được cả vốn lẫn lãi là 19,683 triệu đồng theo phương thức lãi kép?
- A. 0,75%
- B. 0,65%
- C. 9%
- D. 8%
-
Câu 25: Mã câu hỏi: 48751
Thể tích của khối lập phương \(ABCD.A'B'C'D'\) bằng bao nhiêu nếu biết khoảng cách giữa hai đường thẳng \(A'C\) và \(C'D'\) là \(\sqrt 2 :\)
- A. \(8\)
- B. \(2\sqrt 2 .\)
- C. \(3\sqrt 3 .\)
- D. \(27\)
-
Câu 26: Mã câu hỏi: 48752
Cho hàm số \(y = \frac{{x - 2}}{{x + 1}}\). Mệnh đề nào sau đây đúng:
- A. Hàm số nghịch biến trên \(( - \infty ; - 1)\) và \(( - 1; + \infty ) \cdot \)
- B. Hàm số đồng biến trên \(( - \infty ; - 1)\) và \(( - 1; + \infty ) \cdot \)
- C. Hàm số có cực trị.
- D. Đồ thị hàm số không có tiệm cận.
-
Câu 27: Mã câu hỏi: 48753
Hình vẽ bên là đồ thị hàm số nào trong các hàm số đã cho?
.png)
- A. \(y = {x^3} - 3{x^2} + 2.\)
- B. \(y = {x^3} + 3x + 2.\)
- C. \(y = - {x^3} - 3x + 2.\)
- D. \(y = {x^3} - 3x - 2.\)
-
Câu 28: Mã câu hỏi: 48754
Trong các hàm số sau đây, hàm số nào đồng biến trên tập xác định của nó?
- A. \(y = {\left( {\frac{1}{\pi }} \right)^x}.\)
- B. \(y = {\left( {\frac{1}{{\sqrt 3 }}} \right)^x}.\)
- C. \(y = {\left( {\frac{1}{e}} \right)^x}.\)
- D. \(y = {\left( \pi \right)^x}.\)
-
Câu 29: Mã câu hỏi: 48756
Giá trị lớn nhất của hàm số \(y = \frac{{{{\ln }^2}x}}{x}\) trên đoạn \(\left[ {1;{e^3}} \right]\) là:
- A. \(0\)
- B. \(\frac{1}{{{e^3}}} \cdot \)
- C. \(\frac{4}{{{e^2}}} \cdot \)
- D. \(\frac{4}{e} \cdot \)
-
Câu 30: Mã câu hỏi: 48757
Số nghiệm của phương trình \({\log _2}x + {\log _2}(x + 3) = 2\):
- A. 0
- B. 3
- C. 1
- D. 2
-
Câu 31: Mã câu hỏi: 48758
Diện tích xung quanh của hình trụ có bán kính đáy bằng \(a\sqrt 3 \) và đường cao \(a\) là:
- A. \(\sqrt 3 \pi {a^2}.\)
- B. \(2\pi {a^2}.\)
- C. \(\pi {a^2}.\)
- D. \(2\sqrt 3 \pi {a^2}.\)
-
Câu 32: Mã câu hỏi: 48759
Hàm số \(y=f(x)\) có bảng biến thiên như hình vẽ. Hỏi đồ thị hàm số \(y=f(x)\) có bao nhiêu đường tiệm cận?
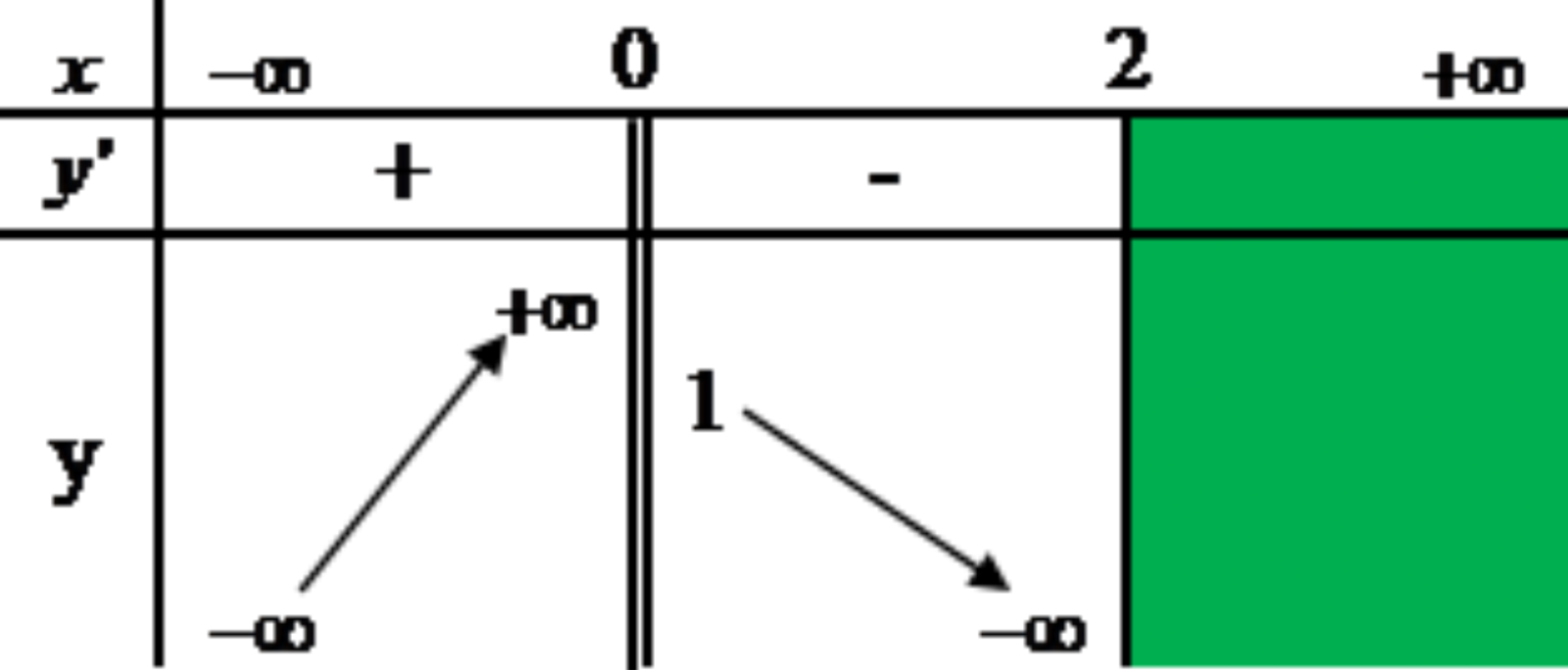
- A. 1
- B. 2
- C. 3
- D. 4
-
Câu 33: Mã câu hỏi: 48760
Hàm số \(y=f(x)\) liên tục và có đạo hàm \(f'(x) > 0\) trên đoạn \([a;b]\). Giá trị lớn nhất của \(y=f(x)\) trên đoạn \([a;b]\) là:
- A. \(f(a)\)
- B. \(f\left( {\frac{{a + b}}{2}} \right).\)
- C. \(f\left( {\frac{{b - a}}{2}} \right).\)
- D. \(f(b)\)
-
Câu 34: Mã câu hỏi: 48761
Hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\). Hai mặt bên \(SAB\) và \(SAC\) cùng vuông góc với đáy, biết \(SB = a\sqrt 3 \). Tính thể tích của khối chóp \(S.ABC\) là:
- A. \(\frac{{{a^3}\sqrt 6 }}{3} \cdot \)
- B. \(\frac{{{a^3}\sqrt 6 }}{4} \cdot \)
- C. \(\frac{{{a^3}\sqrt 6 }}{{12}} \cdot \)
- D. \(\frac{{2{a^3}\sqrt 6 }}{9} \cdot \)
-
Câu 35: Mã câu hỏi: 48762
Hàm số \(y = - {x^4} + 2{x^2} - 3\) đồng biến trên khoảng:
- A. \((1; + \infty ).\)
- B. \((-1;0)\) và \((1; + \infty ).\)
- C. \((-1;0)\)
- D. \(( - \infty ; - 1)\) và \((0;1)\)
-
Câu 36: Mã câu hỏi: 48763
Tất cả các giá trị của \(m\) để hàm số \(y = {({m^2} - 3m + 3)^x}\) đồng biến trên \(R\)?
- A. \(1 < m < 2.\)
- B. \(m>1\)
- C. \(m<2\)
- D. \(m < 1;m > 2.\)
-
Câu 37: Mã câu hỏi: 48764
Hình chóp \(S.ABC\) có \(SA\) vuông góc với mặt phẳng đáy, \(ABC\) là tam giác vuông tại \(B\). Biết \(AB = 3a,BC = 4a\), góc giữa đường thẳng \(SB\) và mặt phẳng \((ABC)\) bằng \(\alpha \) và \(\cos \alpha = \frac{5}{{13}}\). Thể tích khối chóp \(S.ABC\) là:
- A. \(12{a^3}.\)
- B. \(24{a^3}.\)
- C. \(\frac{{72}}{5}{a^3}.\)
- D. \(\frac{{48}}{5}{a^3}.\)
-
Câu 38: Mã câu hỏi: 48765
Đồ thị hàm số \(y = \frac{{x - 1}}{{2x - 1}}\) (C) luôn cắt đường thẳng \(d:y = - x - m\) tại hai điểm \(M, N\) phân biệt. Gọi \({k_1},{k_2}\) lần lượt là hệ số góc của tiếp tuyến của với đồ thị (C) tại \(M, N\). Tìm giá trị của \(m\) để \({k_1} + {k_2}\) đạt giá trị lớn nhất?
- A. \(m=1\)
- B. \(m=2\)
- C. \(m=-5\)
- D. \(m=-1\)
-
Câu 39: Mã câu hỏi: 48766
Cho một tấm nhôm hình vuông \(MNPQ\) cạnh 12. Người ta muốn cắt một hình thang \(ABCD\) \(\left( {AD\parallel BC;MA = 4,NB = 6} \right)\) như hình vẽ. Tìm tổng \(x + y\left( {x = MD,y = PC} \right)\) để diện tích hình thang \(ABCD\) đạt giá trị nhỏ nhất?
.png)
- A. \(7\)
- B. \(5\)
- C. \(7\sqrt 2 .\)
- D. \(4\sqrt 2 .\)
-
Câu 40: Mã câu hỏi: 48767
Hình lập phương thuộc loại đa diện đều nào trong các loại đã cho sau?
- A. \(\left\{ {4;3} \right\}.\)
- B. \({5;3}\)
- C. \({3;4}\)
- D. \({3;5}\)
-
Câu 41: Mã câu hỏi: 48768
Phương trình: \(\sqrt {1 + {{\log }_9}x} - \sqrt {3{{\log }_9}x} = {\log _3}x - 1\) có bao nhiêu nghiệm nguyên?
- A. 0
- B. 1
- C. 2
- D. 3
-
Câu 42: Mã câu hỏi: 48769
Rút gọn \(A = {10^{2 + 3\log 4}}\) được kết quả là:
- A. \({64.10^2}.\)
- B. \(6040\)
- C. \(640\)
- D. \({10^2}.\)
-
Câu 43: Mã câu hỏi: 48770
Cho hình chóp \(S.ABCD\) có đáy \(ANCD\) là hình vuông cạnh \(2a\sqrt 2 \), \(SA\) vuông với mặt phẳng đáy. Mặt phẳng \((\alpha )\) qua \(A\), vuông góc với \(SC\) và cắt \(SB, SC, SD\) lần lượt tại các điểm \(M, N, P\). Thể tích của khối cầu ngoại tiếp hình chóp \(CMNP\) là:
- A. \(\frac{{32\pi {a^3}}}{3} \cdot \)
- B. \(32\pi {a^3}.\)
- C. \(\frac{{16\pi {a^3}}}{3} \cdot \)
- D. \(16\pi {a^3}.\)
-
Câu 44: Mã câu hỏi: 48771
Đồ thị hàm số nào sau đây có tiệm cận?
- A. \(y = \cot x.\)
- B. \(y = cosx.\)
- C. \(y = 2\sin x + 1.\)
- D. \(y = \sin x.\)
-
Câu 45: Mã câu hỏi: 48772
Lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông cân tại \(B\), \(BA = BC = a\), \(AB'\) tạo với đáy \((A'B'B')\) góc \({60^o}\). Thể tích của khối lăng trụ \(ABC.A'B'C'\) là:
- A. \(\frac{{{a^3}\sqrt 3 }}{6} \cdot \)
- B. \(\frac{{{a^3}\sqrt 3 }}{2} \cdot \)
- C. \({a^3}\sqrt 3 .\)
- D. \(\frac{{{a^3}}}{4} \cdot \)
