Câu hỏi trắc nghiệm (40 câu):
-
Câu 1: Mã câu hỏi: 369616
Trong mặt phẳng với hệ tọa độ \(Oxy\), đường tròn tâm \(I\left( {1;3} \right)\) tiếp xúc với đường thẳng \(\Delta :3x + 4y = 0\) thì có bán kính bằng bao nhiêu ?
- A. \(3\)
- B. \(\frac{3}{5}.\)
- C. \(1\)
- D. \(15\)
-
Câu 2: Mã câu hỏi: 369617
Trong mặt phẳng với hệ tọa độ \(Oxy\), lập phương trình đường tròn \((C)\) có tâm \(I\left( {2; - 3} \right)\)và có bán kính \(R = 4\).
- A. \({\left( {x + 2} \right)^2} + {\left( {y - 3} \right)^2} = 16\).
- B. \({\left( {x + 2} \right)^2} + {\left( {y - 3} \right)^2} = 4\).
- C. \({\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} = 4\).
- D. \({\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} = 16\).
-
Câu 3: Mã câu hỏi: 369618
Trong mặt phẳng với hệ tọa độ \(Oxy\), cho đường tròn \((C):{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 4\). Khẳng định nào đúng ?
- A. Đường tròn \(\left( C \right)\) cắt trục \(Ox\) tại hai điểm phân biệt.
- B. Đường tròn \(\left( C \right)\) có bán kính \(R = 4\).
- C. Đường tròn \(\left( C \right)\) có tâm \(I\left( {1; - 2} \right)\).
- D. Đường tròn \(\left( C \right)\) cắt trục \(Oy\) tại hai điểm phân biệt.
-
Câu 4: Mã câu hỏi: 369619
Cho \(\cos \alpha = \frac{1}{3}\). Tính giá trị của \(\cos 2\alpha \).
- A. \(\cos 2\alpha = \frac{2}{3}.\)
- B. \(\cos 2\alpha = - \frac{7}{9}.\)
- C. \(\cos 2\alpha = \frac{7}{9}.\)
- D. \(\cos 2\alpha = \frac{1}{3}.\)
-
Câu 5: Mã câu hỏi: 369620
Trong mặt phẳng với hệ tọa độ \(Oxy\), cho đường thẳng \(d:x - 5y + 3 = 0\). Vectơ có tọa độ nào sau đây là vectơ pháp tuyến của đường thẳng \(d\)?
- A. \(\left( {5; - 1} \right)\).
- B. \(\left( {1; - 5} \right)\). .
- C. \(\left( {1;5} \right)\).
- D. \(\left( {5;1} \right)\).
-
Câu 6: Mã câu hỏi: 369621
Biết \(\tan \alpha = \frac{1}{2}\). Tính \(\cot \alpha \).
- A. \(\cot \alpha = 2\).
- B. \(\cot \alpha = \sqrt 2 \).
- C. \(\cot \alpha = \frac{1}{2}\).
- D. \(\cot \alpha = \frac{1}{4}\).
-
Câu 7: Mã câu hỏi: 369622
Trong mặt phẳng với hệ tọa độ \(Oxy\), điểm \(I\left( {1; - 3} \right)\) là tâm của đường tròn có phương trình nào dưới đây?
- A. \({x^2} + {y^2} - 4x + 7y - 8 = 0\).
- B. \({x^2} + {y^2} + 2x - 20 = 0\).
- C. \({x^2} + {y^2} - 6x - 2y + 9 = 0\).
- D. \({x^2} + {y^2} - 2x + 6y = 0\).
-
Câu 8: Mã câu hỏi: 369623
Cho \(\sin a = \frac{1}{{\sqrt 2 }},\cos a = \frac{{\sqrt 2 }}{2}\). Tính giá trị của \(\sin 2a\).
- A. \(\frac{2}{{\sqrt 2 }}\).
- B. \(\frac{{\sqrt 2 }}{2}\).
- C. \(1\).
- D. \(\frac{1}{2}\).
-
Câu 9: Mã câu hỏi: 369624
Cho đường tròn \((O)\) đường kính bằng \(10\,{\rm{cm}}\). Tính độ dài cung có số đo \(\frac{{7\pi }}{{12}}.\)
- A. \(\frac{{35\pi }}{6}\,{\rm{cm}}\).
- B. \(\frac{{17\pi }}{3}\,{\rm{cm}}\).
- C. \(\frac{{35\pi }}{{2}}\,{\rm{cm}}\).
- D. \(\frac{{35\pi }}{{12}}\,{\rm{cm}}\).
-
Câu 10: Mã câu hỏi: 369625
Cho hàm số \(f\left( x \right) = a{x^2} + bx + c\) có đồ thị như hình bên.
Tập nghiệm của bất phương trình \(f\left( x \right) \le 0\) là
- A. \(\left[ { - 1;0} \right]\).
- B. \(\left[ { - 3; - 1} \right]\).
- C. \(\left[ { - 3;0} \right]\).
- D. \(\left[ { - 2;0} \right]\).
-
Câu 11: Mã câu hỏi: 369626
Hãy chọn khẳng định sai trong các khẳng định dưới đây.
- A. \(\cos \left( {\pi + \alpha } \right) = - \cos \alpha \).
- B. \(\sin \left( { - \alpha } \right) = - \sin \alpha \).
- C. \(\sin \left( {\pi + \alpha } \right) = - \sin \alpha \).
- D. \(\cos \left( { - \alpha } \right) = - \cos \alpha \).
-
Câu 12: Mã câu hỏi: 369627
Trong mặt phẳng với hệ tọa độ \(Oxy\), đường thẳng \(\Delta :3x - 2y - 7 = 0\) cắt đường thẳng nào sau đây?
- A. \({d_1}:3x + 2y = 0\).
- B. \({d_3}: - 3x + 2y - 7 = 0\).
- C. \({d_4}:6x - 4y - 14 = 0\).
- D. \({d_2}:3x - 2y = 0\).
-
Câu 13: Mã câu hỏi: 369628
Trong mặt phẳng với hệ tọa độ \(Oxy\), cho đường thẳng \(d:x + 2y - 1 = 0.\) Khẳng định nào sau đây sai ?
- A. \(d\) đi qua \(A\left( {1;0} \right).\)
- B. \(d\) nhận vectơ \(\overrightarrow u = \left( {1;2} \right)\) làm vectơ chỉ phương.
- C. \(d\) có hệ số góc \(k = - \frac{1}{2}.\)
- D. \(d\) có phương trình tham số \(\left\{ \begin{array}{l}x = - 3 + 2t\\y = 2 - t\end{array} \right.{\rm{ }}\left( {t \in R} \right).\)
-
Câu 14: Mã câu hỏi: 369629
Cho hàm số \(y = f\left( x \right)\) có đồ thị như bình bên.
Bảng xét dấu của \(f\left( x \right)\) là bảng nào sau đây ?
-
A.
-
B.
-
C.
-
D.
-
A.
-
Câu 15: Mã câu hỏi: 369630
Cho \({\rm{cos }}x = \frac{{\rm{2}}}{{\sqrt {\rm{5}} }}\,\,\,\left( { - \frac{\pi }{2} < x < 0} \right)\) thì \(\sin x\) có giá trị bằng
- A. \(\frac{3}{{\sqrt 5 }}\).
- B. \(\frac{{ - 1}}{{\sqrt 5 }}\).
- C. \(\frac{\pi }{4}\).
- D. \(\frac{{ - 3}}{{\sqrt 5 }}\).
-
Câu 16: Mã câu hỏi: 369633
Trong mặt phẳng với hệ tọa độ \(Oxy\), cho đường thẳng \(d:\left\{ \begin{array}{l}x = 2 + 3t\\y = 5 - 4t\end{array} \right.\). Điểm nào sau đây không thuộc \(d\)?
- A. \(C\left( { - 1;9} \right).\)
- B. \(B\left( { 2;5} \right).\)
- C. \(A\left( {5;3} \right).\)
- D. \(D\left( {8; - 3} \right).\)
-
Câu 17: Mã câu hỏi: 369634
Trong mặt phẳng với hệ tọa độ \(Oxy\), cho đường tròn \(({C_m}):{x^2} + {y^2} - 2mx - 4my - 5 = 0\) (\(m\) là tham số). Biết đường tròn \(({C_m})\) có bán kính bằng 5. Khi đó tập hợp tất cả các giá trị của \(m\) là
- A. \(\left\{ 0 \right\}\).
- B. \(\left\{ { - 1;1} \right\}\).
- C. \(\left\{ { - \sqrt 6 ;\sqrt 6 } \right\}\).
- D. \(\left\{ { - 2;2} \right\}\).
-
Câu 18: Mã câu hỏi: 369635
Trên đường tròn lượng giác, gọi \(M\) là điểm biểu diễn của cung lượng giác \(\alpha = - {15^0}.\) Trong các cung lượng giác biểu diễn bởi điểm \(M\), hãy cho biết cung có số đo dương nhỏ nhất là bao nhiêu?
- A. \({75^0}\).
- B. \({165^0}\).
- C. \({105^0}\).
- D. \({345^0}\).
-
Câu 19: Mã câu hỏi: 369637
Hệ thức nào sau đây là sai?
- A. \({\rm{cos5}}\alpha {\rm{.cos2}}\alpha = \frac{1}{2}\left( {{\rm{cos}}7\alpha + {\rm{cos}}3\alpha } \right).\)
- B. \(\sin 5\alpha \cos 2\alpha = \frac{1}{2}\left( {\sin 3\alpha + \sin 7\alpha } \right).\)
- C. \({\rm{sin6}}\alpha .\sin 2\alpha = \frac{1}{2}\left( {\cos 4\alpha - \cos 8\alpha } \right).\)
- D. \({\rm{cos2}}\alpha {\rm{.sin5}}\alpha = \frac{1}{2}\left( {\sin 7\alpha - \sin 3\alpha } \right).\)
-
Câu 20: Mã câu hỏi: 369639
Trong mặt phẳng với hệ tọa độ \(Oxy\), cho hình vuông \(ABCD\) biết \(A\left( { - 1;3} \right),C\left( {1; - 1} \right)\). Lập phương trình đường tròn ngoại tiếp hình vuông \(ABCD\).
- A. \({x^2} + {\left( {y - 1} \right)^2} = 5\).
- B. \({\left( {x - 4} \right)^2} + {\left( {y - 3} \right)^2} = 25\).
- C. \({x^2} + {\left( {y - 1} \right)^2} = \sqrt 5 \).
- D. \({x^2} + {\left( {y + 1} \right)^2} = 17\).
-
Câu 21: Mã câu hỏi: 369640
Trong mặt phẳng với hệ tọa độ \(Oxy\), cho điểm \(A\left( {1; - 2} \right)\) và \(B\left( {0;3} \right)\). Phương trình nào sau đây là một phương trình tham số của đường thẳng \(AB\)?
- A. \(\left\{ \begin{array}{l}x = 5t\\y = 3 - t\end{array} \right.\).
- B. \(\left\{ \begin{array}{l}x = - t\\y = 3 + 5t\end{array} \right.\).
- C. \(\left\{ \begin{array}{l}x = 1 + 5t\\y = - 2 + t\end{array} \right.\).
- D. \(\left\{ \begin{array}{l}x = - 1 + t\\y = 5 - 2t\end{array} \right.\).
-
Câu 22: Mã câu hỏi: 369642
Trong mặt phẳng với hệ tọa độ \(Oxy\), cho đường tròn \(\left( C \right):{x^2} + {y^2} - 2x + 4y - 20 = 0\). Viết phương trình tiếp tuyến của đường tròn \((C)\) tại điểm \(A\left( { - 2;2} \right)\).
- A. \(3x - 4y - 14 = 0\).
- B. \(4x + 3y + 2 = 0\).
- C. \(3x - 4y - 11 = 0\).
- D. \(3x - 4y + 14 = 0\).
-
Câu 23: Mã câu hỏi: 369645
Trong mặt phẳng với hệ tọa độ \(Oxy\), cho hai đường thẳng \({\Delta _1}:\left\{ \begin{array}{l}x = - 2 + mt\\y = 3 - 5t\end{array} \right.\) và \({\Delta _2}:\left( {m + 1} \right)x + my - 5 = 0\) (\(m\) là tham số). Tìm tổng tất cả các giá trị của tham số \(m\) để \({\Delta _1}\) vuông góc với \({\Delta _2}\).
- A. \(4\).
- B. \( - 4\).
- C. \( - 5\).
- D. \(5\).
-
Câu 24: Mã câu hỏi: 369646
Trong mặt phẳng với hệ tọa độ \(Oxy\), cho tam giác \(ABC\) có \(A\left( {1;0} \right),\)\(B\left( {2; - 1} \right),\)\(C\left( {3;5} \right)\). Phương trình của đường cao kẻ từ \(A\) của tam giác \(ABC\) là
- A. \(x + 6y - 1 = 0\).
- B. \(6x + y - 6 = 0\).
- C. \(6x - y - 13 = 0\).
- D. \(6x - y - 6 = 0\).
-
Câu 25: Mã câu hỏi: 369648
Trong mặt phẳng với hệ tọa độ \(Oxy\), cho đường thẳng \(\Delta :3x + y + 6 = 0\) và điểm \(M\left( {1;3} \right).\) Viết phương trình đường thẳng \(d\) biết \(d\) đi qua \(M\) và song song đường thẳng \(\Delta \).
- A. \(x - 3y + 8 = 0\).
- B. \( - 3x + y = 0\).
- C. \(3x + y + 6 = 0\).
- D. \(3x + y - 6 = 0\).
-
Câu 26: Mã câu hỏi: 369649
Trên đường tròn lượng giác (gốc \(A\)), cung lượng giác có số đo \(\alpha = - {90^0} + k{360^0}\,\,\,(k \in Z)\) có điểm cuối trùng với điểm nào sau đây ?
- A. Điểm \(B'\).
- B. Điểm \(A'\).
- C. Điểm\(A\).
- D. Điểm \(B\).
-
Câu 27: Mã câu hỏi: 369650
Cho biểu thức \(P = 3{\sin ^2}x + 2\sin x.\cos x - {\cos ^2}x{\rm{ }}\left( {x \ne \frac{\pi }{2} + k\pi ,k \in Z} \right)\), nếu đặt \(t = \frac{{\sin x}}{{\cos x}}\) thì biểu thức \(P\) được viết theo \(t\) là biểu thức nào dưới đây ?
- A. \(P = 3{t^2} + 2t.\)
- B. \(P = 3{t^2} + 2t - 1.\)
- C. \(P = \frac{{3{t^2} + 2t - 1}}{{{t^2} + 1}}.\)
- D. \(P = \left( {3{t^2} + 2t - 1} \right)\left( {{t^2} + 1} \right).\)
-
Câu 28: Mã câu hỏi: 369652
Trong mặt phẳng với hệ tọa độ \(Oxy\), cho hai điểm \(A\left( {5; - 3} \right)\) và \(B\left( {8;2} \right)\). Viết phương trình đường thẳng \(\Delta \) đi qua \(A\) và có khoảng cách từ \(B\) đến \(\Delta \) lớn nhất.
- A. \(3x + 5y - 34 = 0\).
- B. \(5x - 3y - 34 = 0\).
- C. \(3x + 5y = 0\).
- D. \(5x - 3y = 0\).
-
Câu 29: Mã câu hỏi: 369659
Trên đường tròn lượng giác gốc \(A\), số đo của cung lượng giác nào sau đây có các điểm biểu diễn là cả bốn điểm \(A,{\rm{ }}A',{\rm{ }}B,{\rm{ }}B'\) như hình bên ?
- A. \(\frac{{k\pi }}{4},{\rm{ }}k \in Z\).
- B. \(\frac{{k\pi }}{2},{\rm{ }}k \in Z\).
- C. \(\frac{\pi }{2} + k\pi ,{\rm{ }}k \in Z\).
- D. \(k\pi ,{\rm{ }}k \in Z\).
-
Câu 30: Mã câu hỏi: 369660
Chủ một rạp chiếu phim ước tính, nếu giá mỗi vé xem phim là \(x\) (ngàn đồng) thì lợi nhuận bán vé được tính theo công thức \(P\left( x \right) = - 50{x^2} + 3500x - 2500\) (ngàn đồng). Hỏi muốn lợi nhuận bán vé tối thiểu là 50 triệu đồng thì giá tiền mỗi vé là bao nhiêu?
- A. \(21 \le x \le 48\) (ngàn đồng).
- B. \(21 \le x \le 49\) (ngàn đồng).
- C. \(22 \le x \le 48\) (ngàn đồng).
- D. \(22 \le x \le 49\) (ngàn đồng).
-
Câu 31: Mã câu hỏi: 369663
Trong mặt phẳng với hệ tọa độ \(Oxy\), viết phương trình của đường thẳng \(d\) biết \(d\) vuông góc với đường thẳng \(\Delta :2x - y + 1 = 0\) và cắt đường tròn \(\left( C \right):{x^2} + {y^2} + 2x - 4y - 4 = 0\) theo một dây cung có độ dài bằng 6.
- A. \(x + 2y - 3 = 0\).
- B. \(2x - y + 4 = 0\).
- C. \(2x + y = 0\).
- D. \(x + 2y + 3 = 0\).
-
Câu 32: Mã câu hỏi: 369665
Miền biểu diễn nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}y \ge - 2\\x \ge 2\\2x + y \le 8\end{array} \right.\) có diện tích bằng bao nhiêu?
- A. \(18.\)
- B. \(25.\)
- C. \(4.\)
- D. \(9.\)
-
Câu 33: Mã câu hỏi: 369669
Phần tô đậm trong hình vẽ dưới đây (có chứa biên), biểu diễn tập nghiệm của bất phương trình nào trong các bất phương trình sau?
- A. \(1 < x < 2.\)
- B. \(1 < y < 2.\)
- C. \(1 \le x \le 2.\)
- D. \(1 \le y \le 2.\)
-
Câu 34: Mã câu hỏi: 369670
Trong mặt phẳng với hệ tọa độ \(Oxy\), cho đường thẳng đi qua hai điểm \(A\left( {1;2} \right)\), \(B\left( {4;6} \right)\), tìm tọa độ điểm \(M\) trên trục \(Oy\) sao cho diện tích \(\Delta MAB\) bằng 1.
- A. \(\left( {0;0} \right)\) và \(\left( { - 1;0} \right).\)
- B. \(\left( {0;0} \right)\) và \(\left( {0;\frac{4}{3}} \right).\)
- C. \(\left( {0; - 1} \right)\) và \(\left( {0;\frac{4}{3}} \right)\).
- D. \(\left( {0;\frac{2}{3}} \right)\) và \(\left( { - \frac{1}{2};0} \right)\).
-
Câu 35: Mã câu hỏi: 369672
Trong mặt phẳng với hệ tọa độ \(Oxy\), cho điểm \(M\left( {1;2} \right)\) và đường thẳng \(d:2x + y - 5 = 0\). Toạ độ của điểm đối xứng với điểm \(M\) qua \(d\) là
- A. \(\left( { - \frac{2}{5};\frac{6}{5}} \right)\).
- B. \(\left( {0;\frac{3}{5}} \right)\).
- C. \(\left( {\frac{9}{5};\frac{{12}}{5}} \right)\).
- D. \(\left( {\frac{3}{5}; - 5} \right)\).
-
Câu 36: Mã câu hỏi: 369675
Rút gọn biểu thức \(A = \frac{{\sin 2\alpha + \sin \alpha }}{{1 + \cos 2\alpha + \cos \alpha }}\) (với \(\alpha \) làm cho biểu thức xác định).
- A. \(2\cos \alpha + 1.\)
- B. \(\tan \alpha .\)
- C. \(2\tan \alpha .\)
- D. \(\cot \alpha .\)
-
Câu 37: Mã câu hỏi: 369678
Trong mặt phẳng với hệ tọa độ \(Oxy\), cho các điểm \(A,B,C,M,N,P\) như hình vẽ. Điểm nào dưới đây thuộc đường tròn ngoại tiếp tam giác \(ABC\)?
- A. Điểm \(P\).
- B. Điểm \(O\).
- C. Điểm \(N\).
- D. Điểm \(M\).
-
Câu 38: Mã câu hỏi: 369683
Cho hai tam giác vuông \(OAB\) và \(OCD\) như hình vẽ. Biết \(OB = CD = a\), \(AB = OD = b.\) Tính \(\cos \angle AOC\) theo \(a\) và \(b\).
- A. \(\frac{{2ab}}{{{a^2} + {b^2}}}\).
- B. \(\frac{{{b^2} - {a^2}}}{{{a^2} + {b^2}}}\).
- C. \(1\).
- D. \(\frac{{{a^2} - {b^2}}}{{{a^2} + {b^2}}}\).
-
Câu 39: Mã câu hỏi: 369687
Tìm tất cả các giá trị của tham số \(m\) để bất phương trình \(\left( {m - 1} \right){x^2} - 2\left( {m + 1} \right)x + 2m + 5 > 0\) nghiệm đúng \(\forall x \in R\).
- A. \(m > 1\)
- B. \(m < - 3\)
- C. \( - 3 < m < 2\)
- D. \(m > 2\)
-
Câu 40: Mã câu hỏi: 369688
Cho phương trình \({x^2} - 2(m - 2)x + 4 - 7m = 0\) (\(m\) là tham số). Tìm \(m\) để phương trình có hai nghiệm phân biệt \({x_1},\,{x_2}\) thỏa mãn \(x_1^2 + \,x_2^2 = 10\).
- A. \(m = 1\)
- B. \(m = - \frac{1}{2}\)
- C. \(m = 2\)
- D. \(m = - 4\)





.JPG)
.JPG)

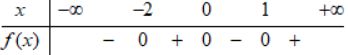
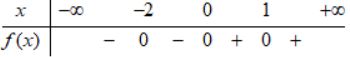

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)

