Bài tập 34-35.10 trang 86 SBT Vật lý 10
Người ta dùng một thanh sắt tròn có độ dài ban đầu l0= 50 cm và tiết diện ngang S = 2,5 mm2. Kéo dãn thanh sắt bằng lực F có cường độ tăng dần và đo độ dãn dài Δl tương ứng của nó (Bảng 34-35.1).
a) Tính độ dãn dài tỉ đối ε của thanh sắt và ứng suất σ của lực kéo tác dụng lên nó trong mỗi lần đo (Bảng 34-35. 1).
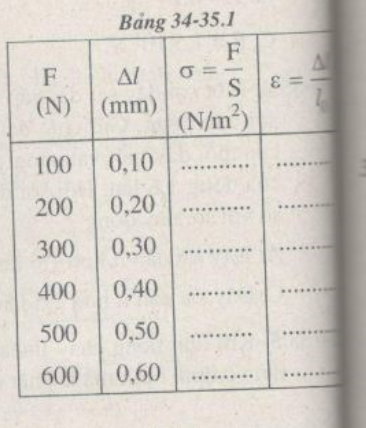
b) Vẽ đồ thị biểu diễn sự phụ thuộc của ε vào σ.
c) Dựa vào đồ thị vẽ được, tìm giá trị của suất đàn hồi E và hệ số đàn hồi k.
Hướng dẫn giải chi tiết
a) Tính độ dãn dài tỉ đối ε của thanh sắt và ứng suất σ của lực kéo tác dụng lên thanh sắt trong mỗi lần đo.
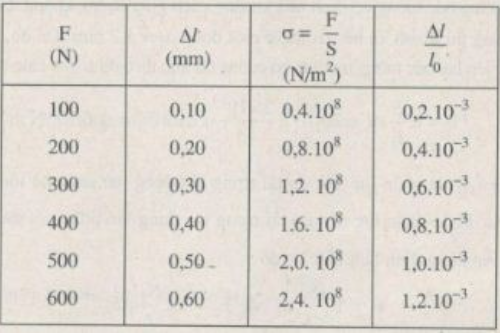
b) Vẽ đồ thị biểu diễn sự phụ thuộc của ε vào σ.
Chọn tỉ lệ vẽ trên các trục tọa độ:
- Trục hoành: 1 cm → σ = 0,5.108 N/m2.
- Trục tung: 1 cm → ε = 0,2.10-3.
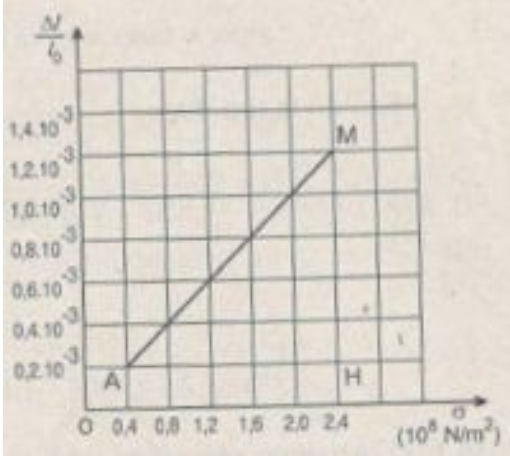
Đồ thị có dạng đường thẳng chứng tỏ độ biến dạng tỉ đối Δl/l0 của thanh sắt tỉ lệ thuận với ứng suất σ của lực kéo tác dụng lên thanh sắt, nghĩa là:
\(\varepsilon = \frac{{{\rm{\Delta }}l}}{{{l_0}}} = a\varepsilon \)
Hệ số tỉ lệ a được xác định bởi hệ số góc của đường biểu diễn đồ thị:
\(\begin{array}{l} \tan \theta = \frac{{MH}}{{AH}}\\ = \frac{{{{1,2.10}^{ - 3}} - {{0,2.10}^{ - 3}}}}{{{{2,4.10}^8} - {{0,4.10}^8}}} = {0,5.10^{ - 11}} \end{array}\)
c) Tìm giá trị của suất đàn hồi E và hệ số đàn hồi k của thanh sắt.
Theo định luật Húc: \(F = k\left| {{\rm{\Delta }}l} \right| = E\frac{S}{{{l_0}}}{\rm{\Delta }}l\)
ta suy ra: \(\frac{{{\rm{\Delta }}l}}{{{l_0}}} = \frac{1}{E}.\frac{F}{S}\)
Từ đó tìm đươc suất đàn hồi :
\(E = \frac{1}{{\tan \theta }} = \frac{1}{{{{0,5.10}^{ - 11}}}} = {20.10^{10}}Pa\)
và hệ số đàn hồi:
\(k = E\frac{S}{{{l_0}}} = {20.10^{10}}.\frac{{{{2,5.10}^{ - 6}}}}{{{{50.10}^{ - 2}}}} = {1.10^6}N/m\)
-- Mod Vật Lý 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





