Nß╗Öi dung b├Āi hß╗Źc B├Āi 29: ─Éß╗ŗnh luß║Łt bß║Żo to├Ān ─æß╗Öng lŲ░ß╗Żng m├┤n Vß║Łt L├Į 10 chŲ░ŲĪng tr├¼nh SGK Kß║┐t nß╗æi tri thß╗®c ─æŲ░ß╗Żc HOC247 tr├¼nh b├Āy b├¬n dŲ░ß╗øi ─æ├óy sß║Į gi├║p c├Īc em t├¼m hiß╗āu vß╗ü ─Éß╗Öng lŲ░ß╗Żng v├Ā ─æß╗ŗnh luß║Łt bß║Żo to├Ān ─æß╗Öng lŲ░ß╗Żng. Nß╗Öi dung chi tiß║┐t mß╗Øi c├Īc em c├╣ng tham khß║Żo b├¬n dŲ░ß╗øi ─æ├óy nh├®!
T├│m tß║»t l├Į thuyß║┐t
1.1. ─Éß╗ŗnh luß║Łt bß║Żo to├Ān ─æß╗Öng lŲ░ß╗Żng
a. Hß╗ć k├Łn (hay hß╗ć c├┤ lß║Łp)
- Mß╗Öt hß╗ć nhiß╗üu vß║Łt ─æŲ░ß╗Żc gß╗Źi l├Ā hß╗ć k├Łn khi kh├┤ng c├│ ngoß║Īi lß╗▒c t├Īc dß╗źng l├¬n hß╗ć hoß║Ęc nß║┐u c├│ th├¼ c├Īc lß╗▒c ß║źy c├ón bß║▒ng nhau. Trong mß╗Öt hß╗ć k├Łn, chß╗ē c├│ c├Īc nß╗Öi lß╗▒c (c├Īc lß╗▒c t├Īc dß╗źng giß╗»a c├Īc vß║Łt trong hß╗ć) tŲ░ŲĪng t├Īc giß╗»a c├Īc vß║Łt. C├Īc nß╗Öi lß╗▒c n├Āy theo ─æß╗ŗnh luß║Łt 3 Newton thß╗▒c ─æß╗æi nhau tß╗½ng ─æß╗Ģi mß╗Öt.
b. ─Éß╗ŗnh luß║Łt bß║Żo to├Ān ─æß╗Öng lŲ░ß╗Żng
- X├®t mß╗Öt hß╗ć k├Łn gß╗ōm hai vß║Łt trŲ░ß╗Żt tr├¬n mß╗Öt ─æß╗ćm kh├Ł ─æß║┐n va chß║Īm vß╗øi nhau. V├¼ c├Īc lß╗▒c \(\overrightarrow {{F_1}} \) v├Ā \(\overrightarrow {{F_2}} \) l├Ā cß║Ęp nß╗Öi lß╗▒c trß╗▒c ─æß╗æi nhau, n├¬n theo ─æß╗ŗnh luß║Łt III Newton, ta viß║┐t:
\(\overrightarrow {{F_1}} \) = - \(\overrightarrow {{F_2}} \) (29.1)
- DŲ░ß╗øi t├Īc dß╗źng cß╗¦a c├Īc lß╗▒c \(\overrightarrow {{F_1}} \) v├Ā \(\overrightarrow {{F_2}} \), trong khoß║Żng thß╗Øi gian \(\Delta t\), ─æß╗Öng lŲ░ß╗Żng cß╗¦a mß╗Śi vß║Łt c├│ ─æß╗Ö biß║┐n thi├¬n lß║¦n lŲ░ß╗Żt l├Ā \(\Delta \overrightarrow {{p_1}} \) v├Ā \(\Delta \overrightarrow {{p_2}} \)
- ├üp dß╗źng c├┤ng thß╗®c \(\overrightarrow {{F}} \Delta t = \Delta \overrightarrow p \) cho tß╗½ng vß║Łt, ta c├│:
\(\left\{ \begin{array}{l}
\overrightarrow {{F_1}} \Delta t = \Delta \overrightarrow {{p_1}} \\
\overrightarrow {{F_2}} \Delta t = \Delta \overrightarrow {{p_2}}
\end{array} \right.\) (29.2)
- Tß╗½ (29.1) v├Ā (29.2), suy ra:
\(\Delta \overrightarrow {{p_1}} = - \Delta \overrightarrow {{p_2}} \) hay \(\Delta \overrightarrow {{p_1}} + \Delta \overrightarrow {{p_2}} = \overrightarrow 0 \)
- Gß╗Źi \(\Delta \overrightarrow {{p_1}} + \Delta \overrightarrow {{p_2}} = \overrightarrow 0 \) l├Ā ─æß╗Öng lŲ░ß╗Żng to├Ān phß║¦n cß╗¦a hß╗ć. Ta c├│ biß║┐n thi├¬n ─æß╗Öng lŲ░ß╗Żng to├Ān phß║¦n cß╗¦a hß╗ć bß║▒ng tß╗Ģng c├Īc biß║┐n thi├¬n ─æß╗Öng lŲ░ß╗Żng cß╗¦a mß╗Śi vß║Łt: \(\Delta \overrightarrow p = \Delta \overrightarrow {{p_1}} + \Delta \overrightarrow {{p_2}} = \overrightarrow 0 \)
- Biß║┐n thi├¬n ─æß╗Öng lŲ░ß╗Żng cß╗¦a hß╗ć bß║▒ng kh├┤ng, ngh─®a l├Ā ─æß╗Öng lŲ░ß╗Żng to├Ān phß║¦n cß╗¦a hß╗ć kh├┤ng ─æß╗Ģi.
\(\overrightarrow p = {\overrightarrow p _1} + {\overrightarrow p _2}\) = kh├┤ng ─æß╗Ģi
- Kß║┐t quß║Ż n├Āy c├│ thß╗ā mß╗¤ rß╗Öng cho hß╗ć k├Łn gß╗ōm nhiß╗üu vß║Łt.
- Tß╗½ ─æ├│, ta c├│ thß╗ā ph├Īt biß╗āu: ─Éß╗Öng lŲ░ß╗Żng to├Ān phß║¦n cß╗¦a hß╗ć k├Łn l├Ā mß╗Öt ─æß║Īi lŲ░ß╗Żng bß║Żo to├Ān.
- Ph├Īt biß╗āu tr├¬n ─æŲ░ß╗Żc gß╗Źi l├Ā ─æß╗ŗnh luß║Łt bß║Żo to├Ān ─æß╗Öng lŲ░ß╗Żng.
- ─Éß╗ŗnh luß║Łt bß║Żo to├Ān ─æß╗Öng lŲ░ß╗Żng c├│ nhiß╗üu ß╗®ng dß╗źng thß╗▒c tß║┐: giß║Żi c├Īc b├Āi to├Īn va chß║Īm, l├Ām cŲĪ sß╗¤ cho nguy├¬n tß║»c chuyß╗ān ─æß╗Öng phß║Żn lß╗▒c.
|
- Mß╗Öt hß╗ć nhiß╗üu vß║Łt t├Īc dß╗źng lß║½n nhau ─æŲ░ß╗Żc gß╗Źi l├Ā hß╗ć k├Łn (hay hß╗ć c├┤ lß║Łp) khi kh├┤ng c├│ ngoß║Īi lß╗▒c t├Īc dß╗źng v├Āo hß╗ć hoß║Ęc khi c├Īc ngoß║Īi lß╗▒c c├ón bß║▒ng nhau. - ─Éß╗ŗnh luß║Łt bß║Żo to├Ān ─æß╗Öng lŲ░ß╗Żng: ŌĆ£─Éß╗Öng lŲ░ß╗Żng to├Ān phß║¦n cß╗¦a hß╗ć k├Łn l├Ā mß╗Öt ─æß║Īi lŲ░ß╗Żng bß║Żo to├ĀnŌĆØ. |
|---|
1.2. Va chß║Īm mß╗üm v├Ā va chß║Īm ─æ├Ān hß╗ōi
C├│ hai kiß╗āu va chß║Īm thŲ░ß╗Øng gß║Ęp l├Ā va chß║Īm ─æ├Ān hß╗ōi v├Ā va chß║Īm mß╗üm.
a. Va chß║Īm ─æ├Ān hß╗ōi
H├¼nh 29.1 m├┤ tß║Ż mß╗Öt th├Ł nghiß╗ćm vß╗ü va chß║Īm ─æ├Ān hß╗ōi.
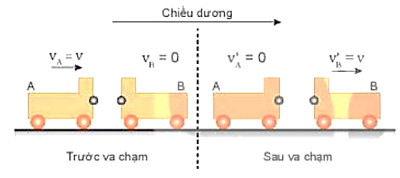
H├¼nh 29.1. Va chß║Īm ─æ├Ān hß╗ōi
- D├╣ng hai xe A v├Ā B giß╗æng nhau, ß╗¤ ─æß║¦u mß╗Śi xe c├│ gß║»n mß╗Öt quß║Ż cß║¦u kim loß║Īi nhß╗Å, cho xe A chuyß╗ān ─æß╗Öng vß╗øi vß║Łn tß╗æc vA = v tß╗øi va chß║Īm vß╗øi xe B─æang ─æß╗®ng y├¬n. Kß║┐t quß║Ż cß╗¦a va chß║Īm l├Ām xe A ─æang chuyß╗ān ─æß╗Öng th├¼ dß╗½ng lß║Īi, c├▓n xe B ─æang ─æß╗®ng y├¬n th├¼ chuyß╗ān ─æß╗Öng vß╗øi ─æ├║ng vß║Łn tß╗æc V'B = v.
- Va chß║Īm nhŲ░ thß║┐ gß╗Źi l├Ā va chß║Īm ─æ├Ān hß╗ōi.
b. Va chß║Īm mß╗üm
- H├¼nh 29.2 m├┤ tß║Ż mß╗Öt th├Ł nghiß╗ćm vß╗ü va chß║Īm mß╗üm.
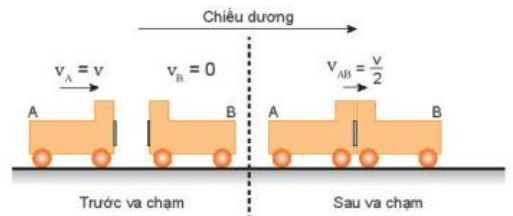
H├¼nh 29.2. Va chß║Īm mß╗üm
- D├╣ng hai xe A v├Ā B giß╗æng nhau, ß╗¤ ─æß║¦u mß╗Śi xe c├│ gß║»n mß╗Öt miß║┐ng nhß╗▒a d├Łnh. Cho xe A chuyß╗ān ─æß╗Öng vß╗øi vß║Łn tß╗æc vA = v tß╗øi va chß║Īm vß╗øi xe kia ─æang ─æß╗®ng y├¬n. Sau va chß║Īm, cß║Ż hai xe d├Łnh v├Āo nhau v├Ā chuyß╗ān ─æß╗Öng vß╗øi vß║Łn tß╗æc bß║▒ng VAB = v/2. Kiß╗āu va chß║Īm ŌĆ£d├ŁnhŌĆØ n├Āy gß╗Źi l├Ā va chß║Īm mß╗üm.
| C├│ hai kiß╗āu va chß║Īm thŲ░ß╗Øng gß║Ęp l├Ā va chß║Īm ─æ├Ān hß╗ōi v├Ā va chß║Īm mß╗üm. |
|---|
B├Āi tß║Łp minh hß╗Źa
B├Āi 1: Mß╗Öt lß╗▒c 50 N t├Īc dß╗źng v├Āo mß╗Öt vß║Łt c├│ khß╗æi lŲ░ß╗Żng m = 0,1 kg ban ─æß║¦u nß║▒m y├¬n; thß╗Øi gian t├Īc dß╗źng l├Ā 0,01 s. X├Īc ─æß╗ŗnh vß║Łn tß╗æc cß╗¦a vß║Łt.
HŲ░ß╗øng dß║½n giß║Żi
*C├Īch 1:
Ta c├│, biß║┐n thi├¬n ─æß╗Öng lŲ░ß╗Żng th├¼ bß║▒ng xung lŲ░ß╗Żng cß╗¦a lß╗▒c:
\(\Delta \overrightarrow p = \overrightarrow F \Delta t \Leftrightarrow m\overrightarrow v - m\overrightarrow {{v_0}} = \overrightarrow F \Delta t\)
Mß║Ęt kh├Īc, theo ─æß║¦u b├Āi ta c├│: \({v_0} = 0m/s\) (do ban ─æß║¦u nß║▒m y├¬n)
Ta suy ra:
\(\begin{array}{l}m\overrightarrow v - \overrightarrow 0 = \overrightarrow F \Delta t \Rightarrow m\overrightarrow v = \overrightarrow F \Delta t\\ \Rightarrow mv = F.\Delta t\\ \Rightarrow v = \dfrac{{F.\Delta t}}{m} = \dfrac{{50.0,01}}{{0,1}} = 5m/s\end{array}\)
*C├Īch 2:
Theo ─æß╗ŗnh luß║Łt II Newton ta c├│:
\(a = \frac{F}{m} = \frac{{50}}{{0,1}} = 500(m/s^2)\)
Lß║Īi c├│: \(v = {v_0} + at = 0 + 500.0,01 = 5(m/s)\)
(vß║Łt ban ─æß║¦u nß║▒m y├¬n n├¬n \({v_0}=0\))
B├Āi 2: Mß╗Öt vß║Łt khß╗æi lŲ░ß╗Żng 0,7 kg ─æang chuyß╗ān ─æß╗Öng theo phŲ░ŲĪng ngang vß╗øi tß╗æc ─æß╗Ö 5 m/s th├¼ va chß║Īm v├Āo bß╗®c tŲ░ß╗Øng thß║│ng ─æß╗®ng. N├│ nß║Ży ngŲ░ß╗Żc trß╗¤ lß║Īi vß╗øi tß╗æc ─æß╗Ö 2 m/s. Chß╗Źn chiß╗üu dŲ░ŲĪng l├Ā chiß╗üu b├│ng nß║Ży ra. ─Éß╗Ö thay ─æß╗Ģi ─æß╗Öng lŲ░ß╗Żng cß╗¦a n├│ l├Ā:
A. 3,5 kg.m/s
B. 24,5 kg.m/s
C. 4,9 kg.m/s
D. 1,1 kg.m/s
HŲ░ß╗øng dß║½n giß║Żi
─Éß╗Ö biß║┐n thi├¬n ─æß╗Öng lŲ░ß╗Żng: ╬öp = p2 - p1 = mv2 - (-mv1)= 4,9 kg.m/s.
B├Āi 3: Mß╗Öt quß║Ż b├│ng c├│ khß╗æi lŲ░ß╗Żng m = 300g va chß║Īm v├Āo tŲ░ß╗Øng v├Ā nß║Ży trß╗¤ lß║Īi vß╗øi c├╣ng vß║Łn tß╗æc. Vß║Łn tß╗æc cß╗¦a b├│ng nŲ░ß╗øc va chß║Īm l├Ā + 5m/s. ─Éß╗Ö biß║┐n thi├¬n ─æß╗Öng lŲ░ß╗Żng cß╗¦a b├│ng l├Ā:
A. 1,5 kg.m/s
B. -3 kg.m/s
C. -1,5 kg.m/s
D. 3 kg.m/s
HŲ░ß╗øng dß║½n giß║Żi
─Éß╗Ö biß║┐n thi├¬n ─æß╗Öng lŲ░ß╗Żng:
Δp = p2 - p1 = - mv - mv = -2mv = -3 kg.m/s.
Luyß╗ćn tß║Łp B├Āi 29 Vß║Łt L├Į 10 KNTT
Sau b├Āi hß╗Źc n├Āy, hß╗Źc sinh c├│ thß╗ā:
- N├¬u ─æŲ░ß╗Żc kh├Īi niß╗ćm hß╗ć c├┤ lß║Łp v├Ā lß║źy v├Ł dß╗ź vß╗ü hß╗ć c├┤ lß║Łp.
- Ph├Īt biß╗āu ─æŲ░ß╗Żc ─æß╗ŗnh luß║Łt bß║Żo to├Ān ─æß╗Öng lŲ░ß╗Żng ─æß╗æi vß╗øi hß╗ć c├┤ lß║Łp.
- Viß║┐t ─æŲ░ß╗Żc biß╗āu thß╗®c cß╗¦a ─æß╗ŗnh luß║Łt bß║Żo to├Ān ─æß╗Öng lŲ░ß╗Żng ─æß╗æi vß╗øi hß╗ć gß╗ōm hai vß║Łt.
3.1. Trß║»c nghiß╗ćm B├Āi 29 m├┤n Vß║Łt L├Į 10 KNTT
C├Īc em c├│ thß╗ā hß╗ć thß╗æng lß║Īi nß╗Öi dung kiß║┐n thß╗®c ─æ├Ż hß╗Źc ─æŲ░ß╗Żc th├┤ng qua b├Āi kiß╗ām tra Trß║»c nghiß╗ćm Vß║Łt L├Į 10 KNTT B├Āi 29 cß╗▒c hay c├│ ─æ├Īp ├Īn v├Ā lß╗Øi giß║Żi chi tiß║┐t.
-
- A. ─æß╗Ö lß╗øn 10kg.m/s; phŲ░ŲĪng thß║│ng ─æß╗®ng chiß╗üu tß╗½ dŲ░ß╗øi l├¬n tr├¬n.
- B. ─æß╗Ö lß╗øn 10.000kg.m/s; phŲ░ŲĪng thß║│ng ─æß╗®ng chiß╗üu tß╗½ tr├¬n xuß╗æng dŲ░ß╗øi.
- C. ─æß╗Ö lß╗øn 10kg.m/s; phŲ░ŲĪng thß║│ng ─æß╗®ng chiß╗üu tß╗½ tr├¬n xuß╗æng dŲ░ß╗øi.
- D. ─æß╗Ö lß╗øn 10.000kg.m/s; phŲ░ŲĪng thß║│ng ─æß╗®ng chiß╗üu tß╗½ dŲ░ß╗øi l├¬n tr├¬n.
-
- A. ─æß╗Ö lß╗øn \(2\sqrt 3 \)kg.m/s; hŲ░ß╗øng xuß╗æng ph├Ła dŲ░ß╗øi tß║Īo vß╗øi phŲ░ŲĪng ngang mß╗Öt g├│c \(\beta \)= 60┬░.
- B. ─æß╗Ö lß╗øn 4kg.m/s; hŲ░ß╗øng xuß╗æng ph├Ła dŲ░ß╗øi tß║Īo vß╗øi phŲ░ŲĪng ngang mß╗Öt g├│c \(\beta \) = 30┬░.
- C. ─æß╗Ö lß╗øn 4kg.m/s; hŲ░ß╗øng xuß╗æng ph├Ła dŲ░ß╗øi tß║Īo vß╗øi phŲ░ŲĪng ngang mß╗Öt g├│c \(\beta \) = 60┬░.
- D. ─æß╗Ö lß╗øn \(2\sqrt 3 \)kg.m/s; hŲ░ß╗øng xuß╗æng ph├Ła dŲ░ß╗øi tß║Īo vß╗øi phŲ░ŲĪng ngang mß╗Öt g├│c \(\beta \) = 30┬░.
-
- A. ─æß╗Ö lß╗øn 0,0314kg.m/s; chiß╗üu l├Ā chiß╗üu ├óm cß╗¦a Ox.
- B. ─æß╗Ö lß╗øn 0,314kg.m/s; chiß╗üu l├Ā chiß╗üu ├óm cß╗¦a Oy.
- C. ─æß╗Ö lß╗øn 0,314kg.m/s; chiß╗üu l├Ā chiß╗üu dŲ░ŲĪng cß╗¦a Oy.
- D. ─æß╗Ö lß╗øn 0,0314kg.m/s; chiß╗üu l├Ā chiß╗üu dŲ░ŲĪng cß╗¦a Ox.
C├óu 4-10: Mß╗Øi c├Īc em ─æ─āng nhß║Łp xem tiß║┐p nß╗Öi dung v├Ā thi thß╗Ł Online ─æß╗ā cß╗¦ng cß╗æ kiß║┐n thß╗®c vß╗ü b├Āi hß╗Źc n├Āy nh├®!
3.2. B├Āi tß║Łp SGK B├Āi 29 m├┤n Vß║Łt L├Į 10 KNTT
C├Īc em c├│ thß╗ā xem th├¬m phß║¦n hŲ░ß╗øng dß║½n Giß║Żi b├Āi tß║Łp Vß║Łt L├Į 10 KNTT B├Āi 29 ─æß╗ā gi├║p c├Īc em nß║»m vß╗»ng b├Āi hß╗Źc v├Ā c├Īc phŲ░ŲĪng ph├Īp giß║Żi b├Āi tß║Łp.
Giß║Żi c├óu hß╗Åi trang 113 SGK Vß║Łt L├Į 10 Kß║┐t nß╗æi tri thß╗®c - KNTT
Giß║Żi c├óu hß╗Åi 1 trang 114 SGK Vß║Łt L├Į 10 Kß║┐t nß╗æi tri thß╗®c - KNTT
Giß║Żi c├óu hß╗Åi 2 trang 114 SGK Vß║Łt L├Į 10 Kß║┐t nß╗æi tri thß╗®c - KNTT
Giß║Żi c├óu hß╗Åi 1 trang 115 SGK Vß║Łt L├Į 10 Kß║┐t nß╗æi tri thß╗®c - KNTT
Giß║Żi c├óu hß╗Åi 2 trang 115 SGK Vß║Łt L├Į 10 Kß║┐t nß╗æi tri thß╗®c - KNTT
Giß║Żi B├Āi tß║Łp 29.1 trang 55 SBT Vß║Łt l├Į 10 Kß║┐t nß╗æi tri thß╗®c - KNTT
Giß║Żi B├Āi tß║Łp 29.2 trang 55 SBT Vß║Łt l├Į 10 Kß║┐t nß╗æi tri thß╗®c - KNTT
Giß║Żi B├Āi tß║Łp 29.3 trang 55 SBT Vß║Łt l├Į 10 Kß║┐t nß╗æi tri thß╗®c - KNTT
Giß║Żi B├Āi tß║Łp 29.4 trang 55 SBT Vß║Łt l├Į 10 Kß║┐t nß╗æi tri thß╗®c - KNTT
Giß║Żi B├Āi tß║Łp 29.5 trang 55 SBT Vß║Łt l├Į 10 Kß║┐t nß╗æi tri thß╗®c - KNTT
Giß║Żi B├Āi tß║Łp 29.6 trang 55 SBT Vß║Łt l├Į 10 Kß║┐t nß╗æi tri thß╗®c - KNTT
Giß║Żi B├Āi tß║Łp 29.7 trang 56 SBT Vß║Łt l├Į 10 Kß║┐t nß╗æi tri thß╗®c - KNTT
Giß║Żi B├Āi tß║Łp 29.8 trang 56 SBT Vß║Łt l├Į 10 Kß║┐t nß╗æi tri thß╗®c - KNTT
Giß║Żi B├Āi tß║Łp 29.9 trang 56 SBT Vß║Łt l├Į 10 Kß║┐t nß╗æi tri thß╗®c - KNTT
Giß║Żi B├Āi tß║Łp 29.10 trang 56 SBT Vß║Łt l├Į 10 Kß║┐t nß╗æi tri thß╗®c - KNTT
Giß║Żi B├Āi tß║Łp 29.11 trang 56 SBT Vß║Łt l├Į 10 Kß║┐t nß╗æi tri thß╗®c - KNTT
Hß╗Åi ─æ├Īp B├Āi 29 m├┤n Vß║Łt L├Į 10 KNTT
Trong qu├Ī tr├¼nh hß╗Źc tß║Łp nß║┐u c├│ thß║»c mß║»c hay cß║¦n trß╗Ż gi├║p g├¼ th├¼ c├Īc em h├Ży comment ß╗¤ mß╗źc Hß╗Åi ─æ├Īp, Cß╗Öng ─æß╗ōng Vß║Łt l├Į HOC247 sß║Į hß╗Ś trß╗Ż cho c├Īc em mß╗Öt c├Īch nhanh ch├│ng!
Ch├║c c├Īc em hß╗Źc tß║Łp tß╗æt v├Ā lu├┤n ─æß║Īt th├Ānh t├Łch cao trong hß╗Źc tß║Łp!
-- Mod Vß║Łt L├Į 10 Hß╗īC247


.jpg)
.jpg)
.jpg)





