Phương pháp giải dạng bài tập về phản xạ toàn phần môn Vật Lý 11 năm 2021-2022

1.1. Định nghĩa

Phản xạ toàn phần là hiện tượng phản xạ toàn bộ tia sáng tới , xảy ra ở mặt phân cách giữa hai môi trường trong suốt

1.2. Điều kiện để có phản xạ toàn phần

- Tia sáng chiếu tới phải truyền từ môi trường chiết quang hơn sang môi trường chiết quang kém .

- Góc tới i \( \ge \) i_gh  (i_gh góc giới hạn toàn phần )

Trong đó : \(\sin {{i}_{gh}}=\frac{{{n}_{2}}}{{{n}_{1}}}=\frac{{{n}_{b}}}{{{n}_{l\acute{i}n}}}\)     

n1 : chiết suất của môi trường tới

n2: chiết suất của môi trường khúc xạ .

Giả sử ban đầu chiếu một tia sáng từ môi trường 1 sang môi trường 2 với n₁ > n₂ \(\Rightarrow r>i\) khi đó sẽ xảy ra các trường hợp :

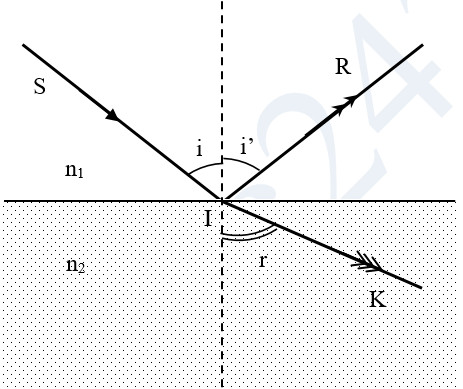
+ Khi góc tới i < i_gh Tia khúc xạ IK còn rất sáng còn tia phản xạ IR rất mờ

_ Khi góc tới  i = i_gh Tia khúc xạ IK nằm ngay trên mặt phân cách và rất mờ còn tia phản xạ IR rất sáng .

Khi i \( \ge \) i_gh : không còn tia khúc xạ . toàn bộ tia tới bị phản xạ ngược lại ban đầu . lúc này tia phản xạ sáng như tia tới.

Hướng dẫn giải

+ Khi ánh sáng truyền từ môi trường (1) sang (2): \({{n}_{1}}\sin i={{n}_{2}}\sin {{30}^{0}}\)   (*)

+ Khi ánh sáng truyền từ môi trường (1) sang (3): \({{n}_{1}}\sin i={{n}_{3}}\sin {{45}^{0}}\)   (**)

+ Từ (*) và (**) ta có: \({{n}_{2}}\sin {{30}^{0}}={{n}_{3}}\sin {{45}^{0}}\Leftrightarrow \frac{{{n}_{2}}}{2}=\frac{{{n}_{3}}}{\sqrt{2}}\Rightarrow \frac{{{n}_{2}}}{{{n}_{3}}}=\sqrt{2}\)   (***)

+ Từ (***) ta thấy \({{n}_{2}}>{{n}_{3}}\) nên chỉ xảy ra phản xạ toàn phần khi ánh sáng truyền từ (2) sang (3).

+ Vậy góc giới hạn phản xạ toàn phần ở mặt phân cách (2) và (3) là:

   \(\sin {{i}_{gh}}=\frac{{{n}_{3}}}{{{n}_{2}}}=\frac{1}{\sqrt{2}}\Rightarrow {{i}_{gh}}={{45}^{0}}\)

Ví dụ 2: Một tấm thủy tinh mỏng, trong suốt, chiết suất n1 = 1,5 có tiết diện là hình chữ nhật ABCD (AB rất lớn so với AD), mặt đáy AB tiếp xúc với một chất lỏng có chiết suất \({{n}_{2}}=\sqrt{2}\). Chiếu tia sáng SI nằm trong mặt phẳng ABCD tới mặt AD sao cho tia tới nằm phía trên pháp tuyến ở điểm tới và tia khúc xạ trong thủy tinh gặp đáy AB ở điểm K. Tính giá trị lớn nhất của góc tới i để có phản xạ toàn phần tại K.    

Hướng dẫn giải

+ Góc giới hạn phản xạ toàn phần:

 \(\sin {{i}_{gh}}=\frac{{{n}_{2}}}{{{n}_{1}}}=\frac{\sqrt{2}}{1,5}\Rightarrow {{i}_{gh}}=70,{{53}^{0}}\)

+ Để tại K xảy ra hiện tượng phản xạ toàn phần thì:

 \({{i}_{1}}\ge {{i}_{gh}}=70,{{53}^{0}}\Rightarrow {{i}_{1-\min }}=70,{{53}^{0}}\)

+ Từ hình vẽ ta có:

\({{r}_{m\text{ax}}}=90-{{i}_{1-\min }}=90-70,53=19,{{47}^{0}}\)

+ Định luật khúc xạ tại I: \(1.\sin i={{n}_{1}}\sin r\)

\(\Rightarrow 1.\sin {{i}_{\max }}={{n}_{1}}\sin {{r}_{\max }}\Rightarrow \sin {{i}_{\max }}=1,5\sin \left( 19,47 \right)=0,5\Rightarrow {{i}_{\max }}={{30}^{0}}\)

Ví dụ 3: Một tia sáng trong thủy tinh đến mặt phân cách giữa thủy tinh với không khí tại điểm I với góc tới i = 300 thì tia phản xạ và khúc xạ vuông góc nhau.

a) Tính chiết suất của thủy tinh.

b) Tính góc tới i để không có tia sáng ló ra không khí tại I.   

Hướng dẫn giải

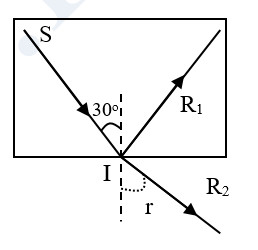
a) Ta có: \(\left\{ \begin{array}{l} {i^/} + 90 + r = 180\\ {i^/} = i = {30^0} \end{array} \right. \Rightarrow r = {60^0}\)

+ Định luật khúc xạ tại I ta có:

\(n\sin 30=1.\sin 60\Rightarrow n=\sqrt{3}\)

b) Để không có tia sáng ló ra không khí tại I thì phải xảy ra hiện tượng phản xạ toàn phần.

+ Góc giới hạn phản xạ toàn phần là: \(\sin {{i}_{gh}}=\frac{{{n}_{kk}}}{{{n}_{tt}}}=\frac{1}{\sqrt{3}}\Rightarrow {{i}_{gh}}=35,{{26}^{0}}\)

+ Vậy điều kiện của góc tới i là \(i\ge {{i}_{gh}}=35,{{26}^{0}}\)

Ví dụ 4: Một khối thủy tinh P có chiết suất n1 = 1,5. Biết tiết diện thẳng là một tam giác ABC vuông cân tại B. Chiếu vuông góc tới mặt AB một chùm sáng song song SI.

a) Khối thủy tinh P ở trong không khí. Tính góc D hợp bởi tia ló và tia tới

b) Tính lại góc D nếu khối P ở trong nước có chiết suất n2 = 4/3

Hướng dẫn giải

a) Tia SI đi đến mặt vuông góc với AB nên truyền thẳng đến mặt AC tại J với góc tới i. Vì ABC vuông cân tại B nên dễ dàng tính được i = 45⁰.

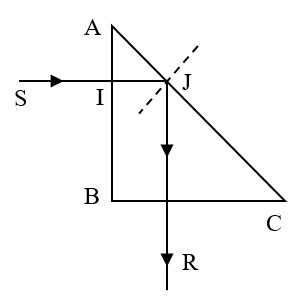
+ Góc giới hạn phản xạ toàn phần là:

\(\sin {{i}_{gh}}=\frac{{{n}_{kk}}}{{{n}_{tt}}}=\frac{1}{1,5}\Rightarrow {{i}_{gh}}=41,{{81}^{0}}\)

+ Vậy tại J xảy ra hiện tượng phản xạ toàn phần với góc phản xạ 45⁰ nên tia phản xạ vuông góc với BC.

+ Vậy góc tạo bởi tia tới SI và tia ló JR ra khỏi lăng kính là D = 90^o.

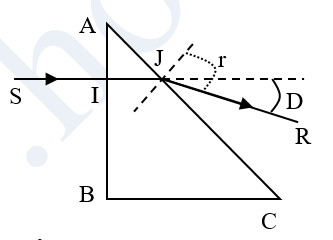
b) Khi khối P ở trong nước thì góc giới hạn phản xạ toàn phần là \(\sin {{i}_{gh}}=\frac{{{n}_{nc}}}{{{n}_{tt}}}=\frac{4/3}{1,5}\Rightarrow {{i}_{gh}}=62,{{73}^{0}}\)

+ Vì tia SI đi vuông góc với AB nên đi thẳng và tới mặt AC tại J với góc tới 45⁰ < i_gh nên có tia khúc xạ tại J. Áp dụng định luật khúc xạ tại J ta có:

\(1,5\sin 45=\frac{4}{3}\sin r\Rightarrow \sin r=0,7955\Rightarrow r=52,{{7}^{0}}\)

+ Từ hình ta tính được góc lệch D lúc này là: D = r – i = 7,7⁰

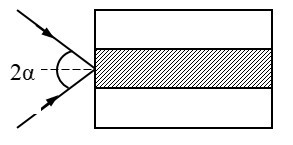
Ví dụ 5: Một ống dẫn sáng hình trụ với lõi có chiết suất n1 = 1,5 và phần bọc ngoài có chiết suất n2 = 1,41. Chùm tia tới hội tụ tại mặt trước của ống với  2a.

Định \(\text{ }\!\!\alpha\!\!\text{ }\) để tia sáng trong chùm đều truyền đi được trong ống.

Hướng dẫn giải

-  Xét đường đi của một tia sáng: SIJK. Để mọi tia sáng đều truyền đi được trong ống (phản xạ toàn phần trên mặt ngoài của lõi) thì góc tới tại J phải thỏa mãn:

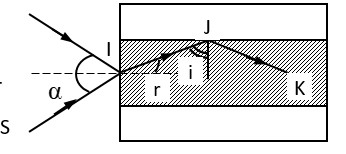
 i \(\ge \) i_gh → sini \(\ge \) sini_gh = \(\frac{{{\text{n}}_{\text{2}}}}{{{\text{n}}_{\text{1}}}}\text{ = }\frac{\text{1,41}}{\text{1,5}}\text{ = 0,94}\)

-  Vì i + r = 90^o → sini = cosr → cosr \(\ge \) 0,94

→ sinr \(\le \) 0,34.

-  Áp dụng định luật khúc xạ tại điểm tới I:

\(\text{sin }\!\!\alpha\!\!\text{  = }{{\text{n}}_{\text{1}}}\text{sinr }\le \text{ 1,5}\text{.0,34}\) = 0,51 Þ \(\text{ }\!\!\alpha\!\!\text{  }\le \text{ 3}{{\text{0}}^{\text{o}}}\)

Vậy: Để tia sáng trong chùm đều truyền đi được trong ống thì \(\text{ }\!\!\alpha\!\!\text{  }\le \text{ 3}{{\text{0}}^{\text{o}}}\).

Ví dụ 6: Một khối nhựa trong suốt hình lập phương, chiết suất n. Định điều kiện mà n phải nghiệm để mọi tia sáng từ không khí xuyên vào một mặt, tới mặt kề đều phản xạ toàn phần trên mặt này.

Hướng dẫn giải

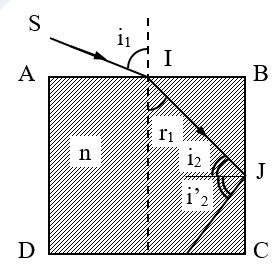
Xét một tiết diện chứa mặt phẳng tới. Theo đề thì tại I có khúc xạ và tại J có phản xạ toàn phần. Ta có:

-  Tại I: sini₁ = nsinr₁ → sinr₁ = \(\frac{\text{sin}{{\text{i}}_{\text{1}}}}{\text{n}}\)   (1)

-  Tại J: sini_gh = \(\frac{\text{1}}{\text{n}}\), i₂ > i_gh.

→ sini₂ > \(\frac{\text{1}}{\text{n}}\) hay cosr₁ > \(\frac{\text{1}}{\text{n}}\) → \(\sqrt{\text{1}-\text{si}{{\text{n}}^{\text{2}}}{{\text{r}}_{\text{1}}}}\) > \(\frac{\text{1}}{\text{n}}\)   (2)

Thay (1) vào (2) ta được: \(\sqrt{\text{1}-\frac{\text{si}{{\text{n}}^{\text{2}}}{{\text{i}}_{\text{1}}}}{{{\text{n}}^{\text{2}}}}}\)> \(\frac{\text{1}}{\text{n}}\) → \(\sqrt{{{\text{n}}^{\text{2}}}-\text{si}{{\text{n}}^{\text{2}}}{{\text{i}}_{\text{1}}}}\) > 1

→ n > \(\sqrt{\text{1+si}{{\text{n}}^{\text{2}}}{{\text{i}}_{\text{1}}}}\)

Vì i_1max = 90^o Þ n > \(\sqrt{\text{1+1}}\text{ = }\sqrt{2}\).

Vậy: Để mọi tia sáng từ không khí xuyên vào một mặt đều phản xạ toàn phần trên mặt bên tiếp theo là n > \(\sqrt{2}\).

Ví dụ 7: Một miếng gỗ mỏng hình tròn, bán kính R = 4 cm. Ở tâm O, cắm thẳng góc một đinh OA. Thả miếng gỗ nổi trong một chậu nước có chiết suất n = 1,33. Đinh OA ở trong nước.

a) Cho OA = 6 cm. Mắt trong không khí sẽ thấy đầu A cách mặt nước bao nhiêu?

b) Tìm chiều dài lớn nhất của OA để mắt không thấy đầu A của đinh.

c) Thay nước bằng một chất lỏng có chiết suất n’. Khi giảm chiều dài OA của đinh tới 3,2 cm thì mắt không thấy được đầu A của đinh nữa. Tính n/.

Hướng dẫn giải

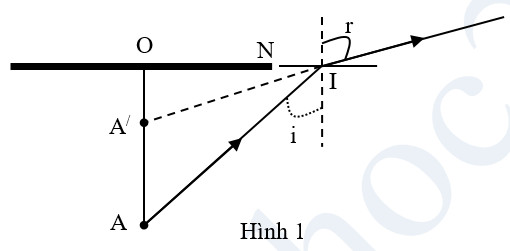
a) Mắt trong không khí thấy tia khúc xạ từ nước ra, do đó mắt quan sát thấy ảnh A^/ của A (xem hình 1)

+ Áp dụng công thức lưỡng chất phẳng ta có: 

\(\frac{O{{A}^{/}}}{OA}=\frac{{{n}_{kx}}}{{{n}_{t}}}=\frac{1}{1,33}\Rightarrow O{{A}^{/}}=4,5\left( cm \right)\)

b) Góc tới giới hạn: \(\sin {{i}_{gh}}=\frac{{{n}_{kk}}}{{{n}_{nc}}}=\frac{1}{\frac{4}{3}}=\frac{3}{4}\Rightarrow {{i}_{gh}}=48,{{59}^{0}}\)

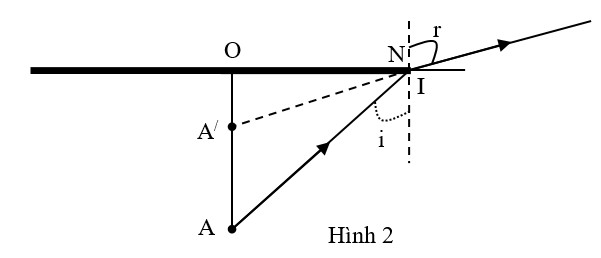
+ Để mắt không thấy đầu A của đinh thì góc tới i ³ i_gh vì lúc đó không có tia khúc xạ từ nước ra không khí. Chiều dài lớn nhất của OA thỏa điều kiện i = i_gh và đồng thời phải bị cạnh của miếng gỗ che lấp (xem hình 2).

Ta có: \(\tan i=\tan {{i}_{gh}}=\frac{ON}{OA}\Rightarrow OA=\frac{ON}{\tan {{i}_{gh}}}=\frac{R}{\tan 48,{{59}^{0}}}=3,53\left( cm \right)\)

c) Tương tự trên ta có: \(\tan i=\frac{ON}{OA}=\frac{4}{3,2}=1,25\)

+ Ta có: \(\cot i=\frac{1}{\tan i}=0,8\).

+ Mà \({{\sin }^{2}}i=\frac{1}{1+{{\cot }^{2}}i}\Rightarrow \sin i=\frac{1}{\sqrt{1+{{\cot }^{2}}i}}=0,78=\sin {{i}_{gh}}\)

+ Lại có: \(\sin {{i}_{gh}}=\frac{1}{n}\Leftrightarrow 0,78=\frac{1}{n}\Rightarrow n=1,28\) (xem hình 2)

Bài 1. Một đèn chiếu ở trong nước rọi một chùm tia sáng song song lên mặt thoáng của nước, phía trên mặt thoáng là một màn E nằm ngang. Ta sẽ nhận được một vệt sáng trên màn E khi góc tới thỏa mãn điều kiện nào. Biết chiết suất của nước là n = \(\frac{4}{3}\).

Bài 2. Tia sáng đi từ thủy tinh có chiết suất n₁ = 1,5 đến mặt phân cách với nước n₂ = 4/3. Hãy tìm điều kiện của góc tới.

a) Để không có tia khúc xạ vào trong nước.

b) Để có tia khúc xạ vào nước.

Bài 3. Ở đáy một chậu nước, cách mặt nước 10 cm người ta đặt một nguồn sáng điểm S. Cho biết chiết suất của nước là \(\frac{4}{3}\).

a) Vẽ đường đi của tia sáng xuất phát từ S, nghiêng một góc 60⁰ với phương nằm ngang.

b) Đặt một đĩa gỗ tròn trên mặt nước, tâm của đĩa nằm trên đường thẳng đứng đi qua S. Tìm bán kính tối thiểu của đĩa để toàn bộ ánh sáng phát ra từ nguồn không ra khỏi mặt nước được.

Bài 4. Một khối thủy tinh P có chiết suất n đặt trong không khí. Tiết diện thẳng là một tam giác cân ABC vuông tại B. Chiếu vuông góc tới mặt AB một chùm sáng song song SI thì tia sáng đi là là mặt AC. Xác định chiết suất n của khối chất P.

Bài 5. Có 3 môi trường trong suốt. Nếu tia sáng truyền từ môi trường 1 vào môi trường 2 dưới góc tới i thì góc khúc xạ là 30⁰. Nếu tia sáng truyền từ môi trường 1 vào môi trường 3 cũng dưới góc tới i thì góc khúc xạ là 45⁰. Hãy tìm góc giới hạn phản xạ toàn phần ở mặt phân cách giữa môi trường 2 và 3.

Bài 6. Một tia sáng SI truyền từ bán trụ thủy tinh ra không khí như hình vẽ. Biết chiết suất của không khí n₂ » 1, của thủy tinh \({{n}_{1}}=\sqrt{2}\), α = 60⁰.

a) Tìm góc giới hạn phản xạ toàn phần.

b) Tìm góc khúc xạ của tia sáng khi đi ra không khí.

c) Giữ nguyên góc tới đưa khối thủy tinh vào trong nước tính góc khúc xạ, biết chiết suất của nước là \({{n}_{3}}=\frac{4}{3}\).

d) Tìm vận tốc truyền ánh sáng trong thủy tinh, biết vận tốc truyền ánh sáng trong chân không là c = 3.10⁸m/s

Bài 7. Một đĩa tròn mỏng, bằng gỗ, bán kính R = 5 cm nổi trên mặt nước. Ở tâm đĩa có gắn một cây kim, thẳng đứng, chìm trong nước \(\left( n=\frac{4}{3} \right)\). Dù đặt mắt trên mặt thoáng ở đâu cũng không thấy cây kim. Hãy tính chiều dài tối đa của cây kim.

Bài 8. Một khối thủy tinh P có chiết suất \({{n}_{1}}=\sqrt{2}\). Biết tiết diện thẳng là một tam giác ABC vuông cân tại B. Chiếu vuông góc tới mặt AB một chùm sáng song song SI.

a) Khối thủy tinh P ở trong không khí. Tính góc D hợp bởi tia ló và tia tới

b) Tính lại góc D nếu khối P ở trong nước có chiết suất n₂ = 4/3

Bài 9. Một tia sáng đi từ một chất lỏng trong suốt có chiết suất n chưa biết sang không khí với góc tới như hình vẽ. Cho biết a = 60^o, b = 30^o.

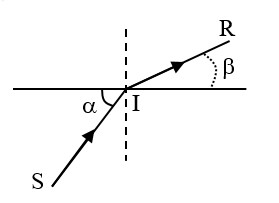
a) Tính chiết suất n của chất lỏng.

b) Tính góc a lớn nhất để tia sáng không thể ló sang môi trường không khí phía trên.    

Bài 10. Chiếu tia sáng đơn sắc từ không khí vào trong chất lỏng trong suốt với góc tới bằng \(i=\frac{\pi }{3}\left( ra\text{d} \right)\) thì góc khúc xạ là \(r=\frac{\pi }{6}\left( ra\text{d} \right)\).

a) Coi tốc độ ánh sáng trong không khí bằng c = 3.10⁸ m/s. Hãy tính tốc độ ánh sáng khi truyền trong chất lỏng.

b) Tìm góc giới hạn phản xạ toàn phần khi chiếu tia sáng trên theo chiều ngược lại.

Bài 11. Có ba môi trường (1), (2), (3). Với cùng một góc tới, nếu ánh sáng đi từ (1) vào (2) thì góc khúc xạ là 30⁰, nếu ánh sáng  đi từ (1) vào (3) thì góc khúc xạ là 45⁰.

a)  Hai môi trường (2) và (3), môi trường nào chiết quang hơn?

b) Tính góc giới hạn phản xạ toàn phần giữa (2) và (3).

Bài 12. Một thợ lặn đứng ở đáy sông nhìn lên mặt nước thì thấy ảnh của những vật ở đáy sông cách mình kể từ khoảng R = 15m.

a)  Giải thích.

b) Cho biết mắt người này ở độ cao 1,5m. Tính độ sâu của sông.

Bài 13. Một khối thủy tinh có tiết diện thẳng như hình vẽ, đặt trong không khí (ABCD: hình vuông; CDE: tam giác vuông cân). Trong mặt phẳng của tiết diện thẳng, chiếu một chùm tia sáng đơn sắc hẹp SI vuông góc với DE (IE < ID).

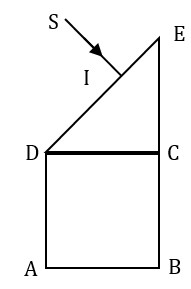
Chiết suất của thủy tinh là n = 1,5. Vẽ tiếp các đường đi của tia sáng trong khối thủy tinh, nếu tia sáng ló ra ngoài thì góc ló bằng bao nhiêu?

Bài 14. Một khối cầu trong suốt, bán kính R làm bằng chất có chiết suất n₂ được đặt trong một môi trường trong suốt chiết quang hơn có chiết suất n₁ (n₂ < n₁). Một tia sáng đơn sắc SI trong môi trường n₁ tới mặt cầu. Gọi l là khoảng cách từ tâm O của mặt cầu đến tia sáng SI.

a) Tìm điều kiện mà l phải thỏa để tia sáng khúc xạ được qua khối cầu.

b) Giả sử điều kiện này được thỏa, hãy tính góc lệch D của tia sáng.

Áp dụng số: R = 2cm, l = 1cm, n₁ = \(\sqrt{3}\), n₂ = 1.

-----( Để xem đầy đủ nội dung của tài liệu, các em vui lòng xem Online hoặc Đăng nhập để tải về máy)------

Trên đây là trích dẫn một phần nội dung tài liệu Phương pháp giải dạng bài tập về phản xạ toàn phần môn Vật Lý 11 năm 2021-2022. Để xem thêm nhiều tư liệu hữu ích khác, các em đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.

Hy vọng tài liệu này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong học tập.