Phương pháp giải dạng bài tập về kính lúp môn Vật Lý 11 năm 2021-2022

+ Kính lúp đơn giản nhất là một thấu kính hội tụ tiêu cự ngắn (cỡ vài cm).

- Cách ngắm chừng:

+ Đặt vật AB trước kính, trong khoảng tiêu cự của kính để có một ảnh ảo A’B’ cùng chiều và lớn hơn vật. Mắt đặt sau kính để quan sát ảnh ảo này. Cần điều chỉnh vị trí vật hay vị trí kính để ảnh ảo này nằm trong giới hạn nhìn rõ của mắt.

+ Nếu điều chỉnh để ảnh ở C_C, ta có ngắm chừng ở điểm cực cận.

+ Nếu điều chỉnh để ảnh ở C_V, ta có ngắm chừng ở điểm cực viễn.

+ Nếu điều chỉnh để ảnh ở vô cực, ta có ngắm chừng ở vô cực.

Số (độ) bội giác của kính lúp: là tỉ số giữa góc trông ảnh (a) qua dụng cụ và góc trông vật (a₀) trực tiếp bằng mắt khi đặt vật ở điểm cực cận.

\(G=\frac{\alpha }{{{\alpha }_{0}}}=\frac{\tan \alpha }{\tan {{\alpha }_{0}}}\)

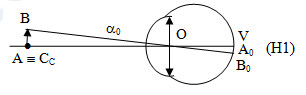
Từ hình vẽ (H1) ta có:

\(\tan {{\alpha }_{0}}=\frac{AB}{O{{C}_{C}}}\,\)

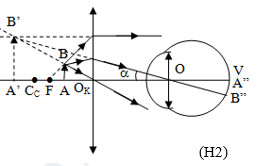
Từ hình vẽ (H2) ta có:

\(\begin{align} & \tan \alpha =\frac{{{A}^{/}}{{B}^{/}}}{O{{A}^{/}}} \\ & \ \ \ \ \ \ \ \ \ =\frac{{{A}^{/}}{{B}^{/}}}{O{{O}_{K}}+{{O}_{K}}{{A}^{/}}}=\frac{{{A}^{/}}{{B}^{/}}}{\ell +\left| {{d}^{/}} \right|}\,\, \\ \end{align}\)

\(\Rightarrow G=\frac{{{A}^{/}}{{B}^{/}}}{AB}\left( \frac{O{{C}_{C}}}{\ell +\left| {{d}^{/}} \right|} \right)=k\left( \frac{O{{C}_{C}}}{\ell +\left| {{d}^{/}} \right|} \right)\)

+ Ngắm chừng ở cực cận thì: \(O{{A}^{/}}=O{{C}_{c}}={{d}^{/}}+\ell \Rightarrow {{G}_{c}}=\frac{{{d}^{/}}}{d}={{k}_{c}}\)

+ Ngắm chừng ở điểm cực viễn thì:  \(O{{A}^{/}}=O{{C}_{v}}={{d}^{/}}+\ell \Rightarrow {{G}_{v}}={{k}_{v}}.\frac{O{{C}_{c}}}{O{{C}_{v}}}\)

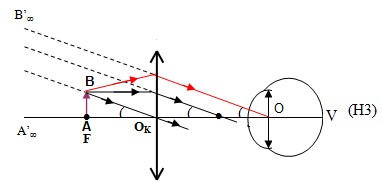
+ Ngắm chừng ở vô cực: \(\tan \alpha =\frac{AB}{f}\Rightarrow {{G}_{\infty }}=\frac{O{{C}_{C}}}{f}=\frac{{{}_{C}}}{f}\) (H 3)

+ Khi trên kính lúp ghi là 8x thì ta hiểu : \(G=8=\frac{0,25}{f}\) (f đo bằng m)

Ví dụ 1: Một kính lúp là thấu kính hội tụ có độ tụ +10dp.

a)  Tính độ bội giác của kính khi ngắm chừng ở vô cực.

b) Tính độ bội giác của kính và độ phóng đại của ảnh khi người quan sát ngắm chừng ở điểm cực cận. Cho biết OC_c = 25cm. Mắt đặt sát kính.

Hướng dẫn giải

a)  Độ bội giác của kính khi ngắm chừng ở vô cực

-   Tiêu cự của kính lúp: f  = \(\frac{1}{D}\)=\(\frac{1}{10}\) = 0,1m = 10cm.

-   Độ bội giác khi ngắm chừng ở vô cực: G\(\infty \) = \(\frac{}{f}\)=\(\frac{O{{C}_{c}}}{f}\) =\(\frac{25}{10}\)= 2,5.

Vậy: Độ bội giác của kính khi ngắm chừng ở vô cực là G\(\infty \) = 2,5.

b) Độ bội giác của kính và độ phóng đại của ảnh khi người quan sát ngắm chừng ở điểm cực cận

-   Khi ngắm chừng ở điểm cực cận thì vật qua kính cho ảnh ảo ở C_c. Sơ đồ tạo ảnh (hình vẽ) :

A \(\xrightarrow{{{\text{O}}_{\text{k}}}\text{ }\equiv \text{ O}}\) A’(ảnh ảo, tại cực cận)

với: d¢ = –O_kC_c = –OC_c = –25cm; f = 10cm.

Suy ra:

d = \(\frac{{d}'f}{{d}'-f}\) = \(\frac{(-25).10}{-25-10}\) = 7,14cm.

-  Độ bội giác của kính và độ phóng đại của ảnh:

G_c = \(\left| k \right|\) = \(\left| -\frac{{{d}'}}{d} \right|\) = \(\left| -\frac{-25}{7,14} \right|\) = 3,5

Vậy: Độ bội giác của kính và độ phóng đại của ảnh khi người quan sát ngắm chừng ở điểm cực cận là G_c = \(\left| \text{k} \right|\) = 3,5.

Ví dụ 2: Một người cận thị có điểm C_c, C_v cách mắt lần lượt 10cm và 50cm. Người này dùng kính lúp có độ tụ +10dp để quan sát một vật nhỏ. Mắt đặt sát kính.

a) Vật phải đặt trong khoảng nào trước kính?

b) Tính độ bội giác của kính và độ phóng đại của ảnh trong các trường hợp:

- Ngắm chừng ở C_v.

- Ngắm chừng ở C­_c.

Hướng dẫn giải

a)  Khoảng đặt vật trước kính

-  Khoảng đặt vật trước kính là MN sao cho ảnh của M, N qua kính lúp là các ảnh ảo lần lượt tại C_c, C_v.

-   Sơ đồ tạo ảnh (hình a và b):

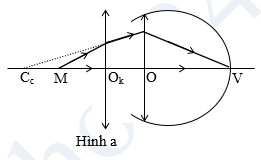
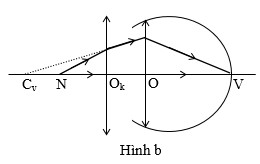
M \(\xrightarrow{{{\text{O}}_{\text{k}}}\text{ }\equiv \text{ O}}\) A₁ (ảnh ảo, tại C_c)

N \(\xrightarrow{{{\text{O}}_{\text{k}}}\text{ }\equiv \text{ O}}\) A₂ (ảnh ảo, tại \({{\text{C}}_{\text{v}}}\))

Ta có: \({{{d}'}_{c}}\) = –O_kC_c = –OC_c = –10cm;

\({{{d}'}_{v}}\)= – O_kC_v = –OC_v = –50cm.                         

f = \(\frac{1}{D}\) = \(\frac{1}{+10}\) = 0,1m = 10cm.

→ d_c = \(\frac{{{{{d}'}}_{c}}f}{{{{{d}'}}_{c}}-f}\) = \(\frac{(-10).10}{-10-10}\) = 5cm

và d_v = \(\frac{{{{{d}'}}_{v}}f}{{{{{d}'}}_{v}}-f}\) = \(\frac{(-50).10}{-50-10}\) = \(\frac{50}{6}\) = 8,3cm.

Vậy: Phải đặt vật trước kính cách mắt từ 5cm đến 8,3cm.

b) Độ bội giác của kính và độ phóng đại của ảnh

-  Khi ngắm chừng ở điểm cực viễn C_v:

+  Độ phóng đại của ảnh: k_v = –\(\frac{{{{{d}'}}_{v}}}{{{d}_{v}}}\) = –\(\frac{-50}{\frac{50}{6}}\) = 6.

+  Độ bội giác của kính: G_v = \(\left| {{k}_{v}} \right|\).\(\frac{}{\left| {{{{d}'}}_{v}} \right|+\ell }\)

với: \(\left| {{{{d}'}}_{v}} \right|+\ell \) = OC_v = 50cm; Đ = 10cm → G_v = 6.\(\frac{10}{50}\) = 1,2

Vậy: Độ phóng đại của ảnh và độ bội giác của kính khi ngắm chừng ở điểm cực cận C_v lần lượt là k_v = 6 và G_v = 1,2.

Ngắm chừng ở điểm cực cận C_c:

+  Độ phóng đại của ảnh: k_c = –\(\frac{{{{{d}'}}_{c}}}{{{d}_{c}}}\) = –\(\frac{-10}{5}\) = 2.

+  Độ bội giác của kính: G_c = k_c.\(\frac{}{\left| {{{{d}'}}_{c}} \right|+\ell }\)

với: Đ = \(\left| {{{{d}'}}_{c}} \right|+\ell \) Þ G_c = k_c = 2.

Vậy: Độ phóng đại của ảnh và độ bội giác của kính khi ngắm chừng ở điểm cực cận C_c là k_c = G_c = 1,2.

Ví dụ 3: Kính lúp có f = 4cm. Mắt người quan sát có giới hạn nhìn rõ từ 11cm đến 65cm. Mắt đặt cách kính 5cm.

a)  Xác định phạm vi ngắm chừng.

b) Tính độ bội giác của kính ứng với trường hợp mắt không điều tiết.

Hướng dẫn giải

a) Phạm vi ngắm chừng

-  Phạm vi ngắm chừng của mắt khi quan sát qua kính lúp là khoảng phải đặt vật trước kính MN sao cho ảnh của M, N qua kính lúp là các ảnh ảo lần lượt tại C_c, C_v.

M \(\xrightarrow{{{\text{O}}_{\text{k}}}}\) M’ (ảnh ảo, tại C_c)

N \(\xrightarrow{{{\text{O}}_{\text{k}}}}\) N’ (ảnh ảo, tại C_v)

Ta có:

\({{{d}'}_{c}}\) = –O_kC_c = –(OC_c – \(\ell \)) = –(11 – 5) = –6cm.

\({{{d}'}_{v}}\)= –O_kC_v = –(OC_v – \(\ell \)) = –(65 – 5) = –60cm.                    

f =  4cm.

Suy ra: d_c = \(\frac{{{{{d}'}}_{c}}f}{{{{{d}'}}_{c}}-f}\) = \(\frac{(-6).4}{-6-4}\) = 2,4cm

d_v = \(\frac{{{{{d}'}}_{v}}f}{{{{{d}'}}_{v}}-f}\) = \(\frac{(-60).4}{-60-4}\) =  3,75cm                   

Vậy: Phạm vi ngắm chừng cách mắt

từ 2,4cm đến 3,75cm.

b) Độ bội giác của kính khi mắt không điều tiết       

-  Để mắt không điều tiết thì phải quan sát ảnh ở điểm cực viễn C_v.

Ta có: G_v = \(\left| {{k}_{v}} \right|\).\(\frac{}{\left| {{{{d}'}}_{v}} \right|+\ell }\)

- Khi ngắm chừng ở điểm cực viễn C_v: \(\left| {{{{d}'}}_{v}} \right|+\ell \) = OC_v = 65cm; Đ = OC_c = 11cm:

\(\left| {{k}_{v}} \right|\)= \(\left| \frac{-{{{{d}'}}_{v}}}{{{d}_{v}}} \right|\) = \(\left| \frac{-60}{3,75} \right|\) = 16 → G_v = 16.\(\frac{11}{65}\) = 2,7

Vậy: Độ bội giác của kính ứng với trường hợp mắt không điều tiết là G_v = 2,7.

Ví dụ 4: Một người đứng tuổi khi nhìn những vật ở xa thì không phải đeo kính nhưng khi đeo kính (sát mắt) có tụ số 1dp thì đọc được trang sách đặt gần nhất là 25cm.

a)  Xác định vị trí của các điểm cực viễn và cực cận của mắt người này.

b) Xác định độ biên thiên của độ tụ mắt người này từ trạng thái không điều tiết đến điều tiết tối đa.

c)  Người này bỏ kính ra và dùng một kính lúp trên vành có ghi X8 để quan sát một vật nhỏ (lấy Đ = 25cm). Mắt cách kính 30cm.

Phải đặt vật trong khoảng nào trước kính? Xác định phạm vi biến thiên của độ bội giác ảnh.

Hướng dẫn giải

a)  Vị trí của các điểm cực viễn và cực cận

-  Điểm cực viễn C_v: Mắt nhìn rõ vật ở xa không đeo kính nên C_v ở xa vô cùng.

-  Điểm cực cận C_c:

+  Tiêu cự của kính: f  = \(\frac{1}{D}\text{ = }\frac{1}{1}\) = 1m = 100cm.

+  Sơ đồ tạo ảnh:  A \(\xrightarrow{{{\text{O}}_{\text{k}}}}\) A’ (ảnh ảo, tại C_c)

Ta có:  d = 25cm; d¢ = –O_kC_c = –OC_c = \(\frac{df}{d-f}\) = \(\frac{25.100}{25-100}\) = –\(\frac{100}{3}\)cm.

Suy ra: OC_c = \(\frac{100}{3}\) = 33,33cm.

Vậy: Điểm cực viễn C_v ở xa vô cực và điểm cực cận C_c cách mắt 33,33cm.

b) Độ biên thiên của độ tụ mắt

-   Độ tụ cực đại của mắt (khi quan sát tại C_c):

D_max = D_c = \(\frac{1}{{{f}_{c}}}\) = \(\frac{1}{O{{C}_{c}}}\) + \(\frac{1}{OV}\)

-   Độ tụ cực tiểu của mắt (khi quan sát tại C_v º \(\infty \)):

D_min = D_v = \(\frac{1}{{{f}_{v}}}\) = \(\frac{1}{O{{C}_{v}}}\) + \(\frac{1}{OV}\) =\(\frac{1}{\infty }\) + \(\frac{1}{OV}\) = \(\frac{1}{OV}\)

-   Độ biến thiên độ tụ của mắt: \(\Delta D\) = D_max – D_min = \(\frac{1}{{{d}_{c}}}\) = \(\frac{1}{\frac{100}{3}}\) = 3dp.

Vậy: Độ biến thiên độ tụ của mắt người này là \(\Delta D\) = 3dp.

c)  Khoảng đặt vật trước kính và phạm vi biến thiên của độ bội giác ảnh

-   Khoảng đặt vật trước kính:

+  Tiêu cự của kính: f  = \(\frac{25}{8}\) = 3,125cm.

+  Sơ đồ tạo ảnh: A \(\xrightarrow{{{\text{O}}_{\text{k}}}}\) A’ (ảnh ảo tại C_c hoặc C_v)

+  Khi quan sát ở C_c:

d¢ = \({{{d}'}_{c}}\) = –O_kC_c = –(OC_c – \(\ell \)) = –(\(\frac{100}{3}\) – 30) = \(\frac{10}{3}\) = –3,33cm.

d = d_c = O_kA = \(\frac{{{{{d}'}}_{c}}f}{{{{{d}'}}_{c}}-f}\) = \(\frac{(-\frac{10}{3}).3,125}{-\frac{10}{3}-3,125}\) = 1,61cm.

+  Khi quan sát ở C_v: d¢ = \({{{d}'}_{v}}\) = –O_kC_v = –(OC_v – \(\ell \)) = – \(\infty \).

d = d_v = f  = 3,125 cm \(\approx \) 3,13cm.

Vậy: Khoảng đặt vật trước kính là 1,61cm \(\le \) d \(\le \) 3,13cm.

-   Phạm vi biến thiên của độ bội giác ảnh

+  Khi ngắm chừng ở C_c: G_c = \(\left| {{k}_{c}} \right|\) = \(\left| -\,\,\frac{{{{{d}'}}_{c}}}{{{d}_{c}}} \right|\) =  \(\left| -\,\,\frac{3,33}{1,61} \right|\) = 2,07.

+  Khi ngắm chừng ở C_{v\(\equiv \infty \)}: G_v = G\(\infty \) = \(\frac{}{f}\) =  \(\frac{O{{C}_{c}}}{f}\) = \(\frac{\frac{100}{3}}{3,125}\) = 10,67.

Vậy: Phạm vi biến thiên của độ bội giác của ảnh là 2,07 \(\le \) G \(\le \) 10,67.

Ví dụ 5: Một người cận thị có điểm cực viễn cách mắt 50cm.

a)  Xác định độ tụ của kính mà người này phải đeo để có thể nhìn rõ một vật ở xa vô cùng không điều tiết.

b) Khi đeo kính, người này có thể đọc được trang sách cách mắt gần nhất là 20cm. Hỏi điểm cực cận của mắt cách mắt bao xa?

c)  Để đọc được những dòng chữ nhỏ mà không phải điều tiết, người này bỏ kính ra và dùng một kính lúp có tiêu cự 5cm đặt sát mắt. Khi đó phải đặt trang sách cách kính lúp bao nhiêu? Tính độ bội giác của ảnh.

Hướng dẫn giải

a)  Độ tụ của kính phải đeo để có thể nhìn rõ vật ở xa vô cùng không điều tiết

Để có thể nhìn rõ vật ở xa vô cùng không điều tiết thì ảnh của vật ở xa vô cùng qua kính phải là ảnh ảo ở điểm cực viễn C_v của mắt. Xét trường hợp kính sát mắt.

-   Sơ đồ tạo ảnh:

 A (vô cực)\(\xrightarrow{{{\text{O}}_{\text{k}}}\text{ }\equiv \text{ O}}\) A’ (ảnh ảo, tại C_v)

 với: d_v = \(\infty \) → f  = \({{{d}'}_{v}}\) =  –OC_v = –50cm = – 0,5m.

-   Độ tụ của kính phải đeo: D = \(\frac{1}{f}\) =\(\frac{1}{-0,5}\)= – 2dp.

Vậy: Độ tụ của kính phải đeo để mắt có thể nhìn rõ vật ở xa vô cùng không điều tiết là D = –2dp (thấu kính phân kì).

b) Điểm cực cận của mắt

-   Ảnh của trang sách đặt gần mắt nhất qua kính là ảnh ảo tại điểm cực cận C_c.

-   Sơ đồ tạo ảnh: A \(\xrightarrow{{{\text{O}}_{\text{k}}}\text{ }\equiv \text{ O}}\)A’ (ảnh ảo, tại C_c)

với: d_c = OA = 20cm; f  = –50cm.

\({{{d}'}_{c}}\) = –OC_c = \(\frac{{{d}_{c}}f}{{{d}_{c}}-f}\) = \(\frac{20.(-50)}{20-(-50)}\) = \(\frac{100}{7}\)= –14,3cm  → OC_c = 14,3cm

Vậy: Điểm cực cận của mắt cách mắt 14,3cm.

c)  Vị trí đặt trang sách khi dùng kính lúp

-   Mắt đọc các dòng chữ nhỏ không điều tiết nên ảnh của trang sách qua kính là ảnh ảo tại điểm cực viễn Cv của mắt.

-   Sơ đồ tạo ảnh:

A \(\xrightarrow{{{\text{O}}_{\text{k}}}\text{ }\equiv \text{ O}}\) A’ (ảnh ảo, tại C_v)

với: d^/ =  –OC_v = –50cm; f  = 5cm.

-  Vị trí đặt trang sách: d = OA =\(\frac{{d}'f}{{d}'-f}\)

d = \(\frac{(-50).5}{(-50)-5}\) = \(\frac{50}{11}\) = 4,55cm

-   Độ bội giác của ảnh

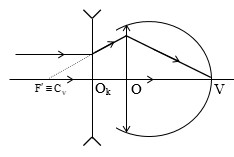
(khi quan sát ở C_v \(\ne \)\(\infty \)):

G = \(\left| k \right|\).\(\frac{}{\left| {{d}'} \right|+\ell }\) = \(\frac{}{O{{C}_{v}}}\), với: \(\left| k \right|\) = \(\left| \frac{{{d}'}}{d} \right|\); \)\ell \) = 0

G = \(\left| \frac{}{d} \right|\) = \(\left| \frac{O{{C}_{c}}}{d} \right|\) = \(\left| \frac{\frac{100}{7}}{\frac{50}{11}} \right|\) = 3,14

Vậy: Phải đặt trang sách cách kính lúp 4,55cm; độ bội giác của ảnh lúc này là G = 3,14.

Bài 1. Một người cận thị có khoảng nhìn rõ ngắn nhất OC_C = 10 cm và giới hạn nhìn rõ là 20 cm. Người này quan sát một vật nhỏ qua kính lúp có tiêu cự 5cm. Kính đeo sát mắt.

a. Phải đặt vật trong khoảng nào trước kính.

b. Tính số bội giác của kính trong các trường hợp người này ngắm chừng ở điểm cực viễn và ở điểm cực cận.

Bài 2. Một kính lúp có độ tụ 50 dp. Mắt có điểm cực cận cách mắt 20 cm đặt tại tiêu điểm ảnh của kính để nhìn vật AB dưới góc trông a = 0,05rad, mắt ngắm chừng ở vô cực.

a. Xác định chiều cao của vật.

b. Đặt mắt cách kính lúp 5cm và ngắm chừng ở điểm cực cận. Tính số bội giác.

Bài 3. Một người mắt bình thường có khoảng nhìn rõ ngắn nhất là 20cm quan sát một vật nhỏ nhờ một kính lúp trên vành ghi 5x. Kính lúp đặt sát mắt.

a. Hỏi vật phải đặt trong khoảng nào trước kính lúp ?

b. Tính số bội giác của kính khi ngắm chừng ở điểm cực cận và ở vô cực.

Bài 4. Một người cận thị có khoảng nhìn rõ ngắn nhất OC_C = 15 cm và giới hạn nhìn rõ là 35 cm. Người này quan sát một vật nhỏ qua kính lúp có tiêu cự 5cm. Mắt đặt cách kính 10 cm.

a. Phải đặt vật trong khoảng nào trước kính.

b. Tính số bội giác của kính trong các trường hợp người này ngắm chừng ở điểm cực viễn và ở điểm cực cận.

Bài 5. Một thợ đồng hồ có giớ hạn nhìn rõ từ 50 cm đến ¥. Người này dùng kính lúp loại 5x để sửa đồng hồ. Kính cách mắt 5 cm.

a. Khi sửa đồng hồ người này phải đặt các chi tiết của đồng hồ cách kính trong giới hạn nào.

b. Tính độ bội giác khi ngắm chừng ở vô cực.

c. Tính độ bội giác khi ngắm chừng ở điểm cực cận.

Bài 6. Một người cận thị có khoảng cách từ mắt đến điểm cực cận là 10cm và đến điểm cực viễn là 50cm, quan sát một vật nhỏ nhờ một kính lúp có tiêu cự f = 4cm. Kính lúp đặt cách mắt 2cm.

a. Phải đặt vật trong khoảng nào trước kính ?

b. Tính số bội giác của kính lúp khi vật đặt trước kính và cách kính 3,5cm.

c. Tính số bội giác của kính lúp khi ngắm chừng ở cực cận.

d. Tính số bội giác của kính lúp khi ngắm chừng ở cực viễn.

Bài 7. Một người mắt bình thường có khoảng nhìn rõ ngắn nhất (khoảng cực cận) là 20cm quan sát một vật nhỏ qua một kính lúp có tiêu cự f = 5cm. Kính đặt cách mắt 10cm.

a. Phải đặt vật trong khoảng nào trước kính ?

b. Tính độ bội giác của kính khi ngắm chừng ở điểm cực cận và ở vô cực.

c. Tính độ bội giác của kính khi vật đặt cách kính 4cm.

d. Phải đặt vật ở vị trí nào để có số (độ) bội giác là 3,5 ?

-----( Để xem đầy đủ nội dung của tài liệu, các em vui lòng xem Online hoặc Đăng nhập để tải về máy)------

Trên đây là trích dẫn một phần nội dung tài liệu Phương pháp giải dạng bài tập về kính lúp môn Vật Lý 11 năm 2021-2022. Để xem thêm nhiều tư liệu hữu ích khác, các em đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.

Hy vọng tài liệu này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong học tập.

Ngoài ra các em có thể tham khảo thêm một số tư liệu cùng chuyên mục sau:

• Phương pháp giải dạng bài tập về phản xạ toàn phần môn Vật Lý 11 năm 2021-2022
• Phương pháp giải bài tập chuyên đề lăng kính môn Vật Lý 11 năm 2021-2022