Dưới đây là Phương pháp giải dạng bài tập liên quan đến khoảng cách vật ảnh môn Vật Lý 11 năm 2021-2022 được HOC247 biên soạn và tổng hợp với nội dung đầy đủ, chi tiết có đáp án cụ thể để các em đối chiếu kết quả bài làm, từ đó tự đánh giá năng lực bản thân, có kế hoạch ôn tập cụ thể, đạt kết quả thật cao trong các kì thi sắp tới. Mời các em cùng tham khảo.
1. PHƯƠNG PHÁP GIẢI
Áp dụng các công thức về ảnh tạo bởi thấu kính:
\(\left\{ \begin{align} & {{d}^{/}}=\frac{df}{d-f} \\ & k=-\frac{{{d}^{/}}}{d}=\frac{f}{f-d} \\ \end{align} \right.\)
Vật và ảnh cùng tính chất thì trái chiều và ngược lại
Trong mọi trường hợp khoảng cách giữa vật và ảnh là: \(L=\left| d+{{d}^{/}} \right|\)
2. VÍ DỤ MINH HỌA
Ví dụ 1: Một màn ảnh đặt song song với vật sáng AB và cách AB một đoạn L. Một thấu kính hội tụ có tiêu cự f đặt trong khoảng giữa vật và màn sao cho AB vuông góc với trục chính của thấu kính. Tìm mối liên hệ giữa L và f để
a. có 2 vị trí của thấu kính cho ảnh rõ nét trên màn.
b. có 1 vị trí của thấu kính cho ảnh rõ nét trên màn.
c. không có vị trí của thấu kính cho ảnh rõ nét trên màn.
Hướng dẫn giải
Vì ảnh hứng trên màn là ảnh thật nên d/ > 0 → \(L=d+{{d}^{/}}\)
Ta có: \(d=\frac{{{d}^{/}}.f}{{{d}^{/}}-f}\Rightarrow L=\frac{{{d}^{/}}.f}{{{d}^{/}}-f}+{{d}^{/}}\)
\(\Leftrightarrow L\left( {{d}^{/}}-f \right)={{\left( {{d}^{/}} \right)}^{2}}\Rightarrow {{\left( {{d}^{/}} \right)}^{2}}-L.{{d}^{/}}+f.L=0\,\,\,\,\,\,\,\left( * \right)\)
Ta có: \(\Delta ={{b}^{2}}-4\text{a}c={{L}^{2}}-4fL\)
a) Để có hai ảnh rõ nét trên màn thì phương trình (*) phải có hai nghiệm phân biệt hay \(\Delta >0\Leftrightarrow {{L}^{2}}-4fL>0\Rightarrow L-4f>0\Rightarrow L>4f\)
b) Để có 1 vị trí của thấu kính cho ảnh rõ nét trên màn thì phương trình (*) phải có nghiệm kép hay \(\Delta =0\Leftrightarrow {{L}^{2}}-4fL=0\Rightarrow L-4f=0\Rightarrow L=4f\)
c) Để không có vị trí của thấu kính cho ảnh rõ nét trên màn thì phương trình (*) phải vô nghiệm hay \(\Delta <0\Leftrightarrow {{L}^{2}}-4fL<0\Rightarrow L-4f<0\Rightarrow L<4f\)
Ví dụ 2: Một vật sáng AB = 4 mm đặt thẳng góc với trục chính của một thấu kính hội tụ có tiêu cự 40 cm, cho ảnh cách vật 36 cm. Xác định vị trí, tính chất và độ lớn của ảnh và vị trí của vật.
Hướng dẫn giải
Ta có: \(L=\left| d+{{d}^{/}} \right|=36\Leftrightarrow d+{{d}^{/}}=\pm 36\)
Ta có: \({{d}^{/}}=\frac{df}{d-f}\Rightarrow L=d+\frac{df}{d-f}=\pm 36\Leftrightarrow {{d}^{2}}=\pm 36\left( d-f \right)\Leftrightarrow {{d}^{2}}=\pm 36\left( d-40 \right)\)
\(\Leftrightarrow {{d}^{2}}=\pm 36\left( d-40 \right)\Rightarrow \left\{ \begin{align} & {{d}^{2}}-36\text{d}+36.40=0\,\,\,\,\,\,\,\,\left( 1 \right) \\ & {{d}^{2}}+36\text{d}-36.40=0\,\,\,\,\,\,\,\,\left( 2 \right) \\ \end{align} \right.\)
Giải (1): \({{d}^{2}}-36\text{d}+36.40=0\Rightarrow \) vô nghiệm
Giải (2):
\({d^2} + 36{\rm{d}} - 36.40 = 0 \Rightarrow \left\{ \begin{array}{l} d = 24\left( {cm} \right)\\ d = - 60\left( {cm} \right){\mkern 1mu} {\mkern 1mu} \end{array} \right.\)
Vị trí ảnh: \({{d}^{/}}=\frac{df}{d-f}=\frac{24.40}{24-40}=-60\left( cm \right)\)< 0 → ảnh ảo
Số phóng đại của ảnh: \(k=-\frac{{{d}^{/}}}{d}\Rightarrow k=-\frac{-60}{24}=2,5>0\) → ảnh cùng chiều với vật.
Độ lớn của ảnh: \({{\text{A}}^{/}}{{B}^{/}}=\left| k \right|AB=2,5.4=10\left( mm \right)\)
Ví dụ 3: Đặt 1 vật sáng AB có chiều cao 2cm trước 1 thấu kính hội tụ có tiêu cự f = 20 cm. Cách vật AB đoạn 90 cm người ta đặt 1 màn hứng.
a. Hãy tìm vị trí đặt thấu kính để có thể hứng ảnh rõ nét trên màn ?
b. Tìm độ cao của ảnh trong câu a ?
Hướng dẫn giải
a) Vì ảnh hứng trên màn nên \(L=d+{{d}^{/}}=90\)
Ta có: \({{d}^{/}}=\frac{df}{d-f}\Leftrightarrow d+{{d}^{/}}=90\Leftrightarrow d+\frac{df}{d-f}=90\)
\(\Leftrightarrow {{d}^{2}}=90\left( d-f \right)\Rightarrow {{d}^{2}}-90\text{d}+90f=0\Leftrightarrow {{d}^{2}}-90\text{d}+1800=0\Rightarrow \left( \begin{align} & {{d}_{1}}=30\left( cm \right) \\ & {{d}_{2}}=60\left( cm \right) \\ \end{align} \right.\)
Vậy phải đặt thấu kính cách vật đoạn 60cm hoặc 30cm
b) Số phóng đại của ảnh khi d1 = 30 cm: \({{k}_{1}}=-\frac{d_{1}^{/}}{{{d}_{1}}}=\frac{\frac{{{d}_{1}}f}{f-{{d}_{1}}}}{{{d}_{1}}}=\frac{f}{f-{{d}_{1}}}=\frac{20}{20-30}=-2\)
Số phóng đại của ảnh khi d2 = 60 cm: \({{k}_{2}}=-\frac{d_{2}^{/}}{{{d}_{2}}}=\frac{\frac{{{d}_{2}}f}{f-{{d}_{2}}}}{{{d}_{2}}}=\frac{f}{f-{{d}_{2}}}=\frac{20}{20-60}=-\frac{1}{2}\)
Ví dụ 4: Một màn ảnh đặt song song với vật sáng AB và cách AB một đoạn L = 72 cm. Một thấu kính hội tụ có tiêu cự f đặt trong khoảng giữa vật và màn sao cho AB vuông góc với trục chính của thấu kính, người ta tìm được hai vị trí của thấu kính cho ảnh rõ nét trên màn. Hai vị trí này cách nhau \(a=48\,\left( cm \right)\). Tính tiêu cự thấu kính.
Hướng dẫn giải
Gọi \({{d}_{1}};\,\,d_{1}^{/}\) là khoảng cách từ vật và ảnh đến thấu kính trước khi di chuyển.
Gọi \({{d}_{2}};\,\,d_{2}^{/}\) là khoảng cách từ vật và ảnh đến thấu kính sau khi di chuyển.
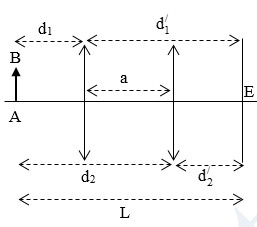
Theo tính thuận nghịch của chiều truyền ánh sáng ta có:
\(\left\{ \begin{array}{l} {d_1} = d_2^/\\ {d_2} = d_1^/ \end{array} \right.\)
Ta lại có:
\(\left\{ \begin{array}{l} {d_1} + d_1^/ = L\\ d_1^/ - {d_1} = a \end{array} \right. \Rightarrow \left\{ \begin{array}{l} {d_1} = \frac{{L - a}}{2}\\ d_1^/ = \frac{{L + a}}{2} \end{array} \right.\)
Lại có: \(\frac{1}{f}=\frac{1}{d}+\frac{1}{{{d}^{/}}}=\frac{2}{L-a}+\frac{2}{L+a}\)
\(\Leftrightarrow \frac{1}{f}=\frac{2}{72-48}+\frac{2}{72+48}\Rightarrow f=10\,\left( cm \right)\)
Ví dụ 5: Vật thật AB đặt cách màn một khoảng L = 90 cm. Trong khoảng giữa vật và màn ta đặt 1 thấu kính, dịch chuyển thấu kính ta thấy có 2 vị trí cho ảnh rõ nét trên màn có độ cao lần lượt là A/B/ = 8 cm, A//B// = 2 cm.
a. Xác định độ cao của vật AB.
b. Tính tiêu cự thấu kính.
Hướng dẫn giải
a) Ta có:
\(\left\{ \begin{array}{l} {d_1} = d_2^/\\ d_1^/ = {d_2} \end{array} \right. \Rightarrow \left\{ \begin{array}{l} {k_1} = - \frac{{d_1^/}}{{{d_1}}}\\ {k_2} = - \frac{{d_2^/}}{{{d_2}}} \end{array} \right. \Rightarrow {k_1}.{k_2} = 1\)
\(\Leftrightarrow \frac{{{A}^{/}}{{B}^{/}}}{AB}.\frac{{{A}^{//}}{{B}^{//}}}{AB}=1\Rightarrow AB=\sqrt{{{A}^{/}}{{B}^{/}}.{{A}^{//}}{{B}^{//}}}=4\left( cm \right)\)
b) Ta có: \(L={{d}_{1}}+d_{1}^{/}={{d}_{1}}+\frac{{{d}_{1}}f}{{{d}_{1}}-f}=90\Rightarrow d_{1}^{2}-90{{\text{d}}_{1}}+90f=0\) (1)
+ Theo bài ra ta có: \(\left| {{k}_{1}} \right|=\frac{{{A}^{/}}{{B}^{/}}}{AB}=\frac{8}{4}=2\left( cm \right)\)
+ Vì ảnh thật nên \({{k}_{1}}<0\Rightarrow {{k}_{1}}=-2\)
+ Lại có: \({{k}_{1}}=-\frac{d_{1}^{/}}{{{d}_{1}}}=\frac{f}{f-{{d}_{1}}}=-2\Rightarrow {{d}_{1}}=1,5f\) (2)
+ Thay (2) vào (1) ta có: \({{\left( 1,5f \right)}^{2}}-90\left( 1,5f \right)+90f=0\)
\(\Rightarrow 1,{{5}^{2}}f-90.1,5+90=0\Rightarrow f=20\left( cm \right)\)
3. LUYỆN TẬP
Bài 1. Thấu kính hội tụ có tiêu cự 24cm. Vật AB được đặt cách màn E một đoạn 108cm. Có hai vị trí của thấu kính trong khoảng giữa vật và màn tạo được ảnh rõ nét của vật trên màn. Xác định hai vị trí của thấu kính.
Bài 2. Một vật sáng AB đặt thẳng góc với trục chính của một thấu kính hội tụ có f = 20 cm cho ảnh thật cách vật 90 cm. Xác định vị trí của vật và ảnh.
Bài 3. Một thấu kính hội tụ có tiêu cự 6 cm. Vật sáng AB là một đoạn thẳng đặt vuông góc trục chính của thấu kính cho ảnh cách vật 25 cm. Xác định vị trí vật và ảnh.
Bài 4. Vật sáng AB đặt song song và cách màn một khoảng 54 cm, giữa vật và màn, người ta đặt 1 thấu kính sao cho thu được ảnh A/B/ hiện rõ trên màn và lớn gấp 2 lần vật.
Hãy cho biết thấu kính trên là thấu kính loại gì ?
Khoảng cách từ vật và ảnh đến thấu kính ?
Tiêu cự của thấu kính nói trên ?
Bài 5. Đặt một vật AB vuông góc với trục chính của 1 thấu kính hội tụ, cho ảnh thật lớn gấp 4 lần vật và cách vật 150cm.
Xác định tiêu cự của thấu kính nói trên ?
Xác định vị trí của ảnh thu được.
Bài 6. Một vật sáng AB cho ảnh thật qua một thấu kính hội tụ L, ảnh này hứng trên một màn E đặt cách vật một khoảng 180 cm, ảnh thu được cao bằng \(\frac{1}{5}\) vật.
Tính tiêu cự của thấu kính.
Giữa nguyên vị trí của AB và màn E. Dịch chuyển thấu kính trong khoảng AB và màn. Có vị trí nào khác của thấu kính để ảnh lại xuất hiện trên màn E không?
Bài 7. Một màn ảnh đặt song song với vật sáng AB và cách AB một đoạn L = 90 cm. Một thấu kính hội tụ có tiêu cự f đặt trong khoảng giữa vật và màn sao cho AB vuông góc với trục chính của thấu kính, người ta tìm được hai vị trí của thấu kính cho ảnh rõ nét trên màn. Hai vị trí này cách nhau \(a=60\,\left( cm \right)\).
Xác định hai vị trí của thấu kính so với vật.
Tính tiêu cự thấu kính.
Bài 8. Một vật sáng AB đặt cố định, song song và cách màn ảnh 1,8m. Một thấu kính hội tụ có tiêu cự f, được đặt trong khoảng giữa vật và màn. Trục chính của thấu kính vuông góc với vật và màn, điểm A nằm trên trục chính.
Cho f = 25cm. Xác định vị trí thấu kính để có ảnh rõ nét trên màn.
Xác định tiêu cự của thấu kính để chỉ có một vị trí của nó ảnh rõ nét trên màn.
-----( Để xem đầy đủ nội dung của tài liệu, các em vui lòng xem Online hoặc Đăng nhập để tải về máy)------
Trên đây là trích dẫn một phần nội dung tài liệu Phương pháp giải dạng bài tập liên quan đến khoảng cách vật ảnh môn Vật Lý 11 năm 2021-2022. Để xem thêm nhiều tư liệu hữu ích khác, các em đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.
Hy vọng tài liệu này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong học tập.
Ngoài ra các em học sinh có thể tham khảo thêm một số tư liệu cùng chuyên mục sau đây:













