Phương pháp giải bài tập về kính thiên văn môn Vật Lý 11 năm 2021-2022

+ Kính thiên văn là dụng cụ quang học bổ trợ cho mắt làm tăng góc trông ảnh của những vật ở rất xa (các thiên thể).

+ Sơ đồ tạo ảnh: \(AB\xrightarrow{{{L}_{1}}}{{A}_{1}}{{B}_{1}}\xrightarrow{{{L}_{2}}}{{A}_{2}}{{B}_{2}}\)

Trong đó ta luôn có: \({{d}_{1}}=\infty \Rightarrow d_{1}^{/}\,={{f}_{1}}\)  (vì A₁ º \(F_{1}^{/}\))

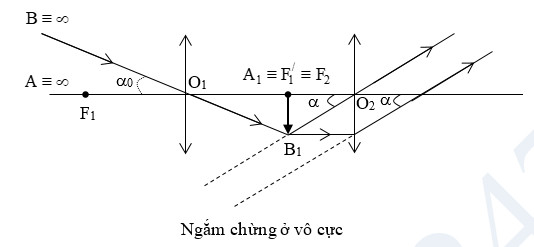
+ Độ bội giác:

- Với kính thiên văn thì \(\tan {{\alpha }_{0}}=\frac{{{A}_{1}}{{B}_{1}}}{{{f}_{1}}}\)

- Ngắm chừng ở vô cực: \({{G}_{\infty }}=\frac{{{f}_{1}}}{{{f}_{2}}}\)

- Ngắm chừng ở một vị trí bất kì: \(\tan \alpha =\frac{{{A}_{1}}{{B}_{1}}}{{{O}_{2}}{{A}_{1}}}=\frac{{{A}_{1}}{{B}_{1}}}{{{d}_{2}}}\Rightarrow G=\frac{{{f}_{1}}}{{{d}_{2}}}\)

- Khi ngắm chừng ở vô cực thì d₂ = f₂.

Lưu ý: Khoảng cách giữa vật kính và thị kính của kính thiên văn thay đổi được và được tính theo công thức: \(a = {f_1} + {d_2}a = {f_1} + {f_2}\)

Ví dụ 1: Vật kính của một kính thiên văn dùng trong nhà trường có tiêu cự f₁ = 1 m, thị kính là một thấu kính hội tụ có tiêu cự f₂ = 4 cm. Tính khoảng cách giữa hai kính và độ bội giác của kính thiên văn khi ngắm chừng ở vô cực.

Hướng dẫn giải

+ Khi ngắm chừng ở vô cực thì \(F_{1}^{/}\equiv {{F}_{2}}\)nên khoảng cách giữa hai kính là:

\(a={{O}_{1}}{{O}_{2}}={{f}_{1}}+{{f}_{2}}=100+4=104\left( cm \right)\)

+ Độ bội giác khi ngắm chừng ở vô cực : \({{G}_{\infty }}=\frac{{{f}_{1}}}{{{f}_{2}}}=\frac{100}{4}=25\)

Ví dụ 2: Vật kính của một kính thiên văn học sinh có tiêu cự f₁ = 120 cm, thị kính có tiêu cự f₂ = 4 cm. Một học sinh có điểm cực viễn cách mắt 50 cm quan sát ảnh của Mặt Trăng qua kính thiên văn nói trên sao cho mắt không điều tiết. Tính khoảng cách giữa hai kính và độ bội giác. Mắt đặt sát sau thị kính

Hướng dẫn giải

+ Mắt quan sát ảnh ảo A₂B₂ ở trạng thái mắt không điều tiết nên A₂B₂ ở cực viễn của mắt tức \(d_{2}^{/}=-{{O}_{2}}{{A}_{2}}=-O{{C}_{v}}=-50cm\)

A₁B₁ cách thị kính: \({{d}_{2}}={{O}_{2}}{{A}_{1}}=\frac{d_{2}^{/}{{f}_{2}}}{d_{2}^{/}-{{f}_{2}}}=\frac{-50.4}{-50-4}\approx 3,7\left( cm \right)\)

+ Khoảng cách giữa hai kính là: \(a={{f}_{1}}+{{d}_{2}}=120+3,7=123,7\left( cm \right)\)

+ Độ bội giác: \({{G}_{v}}=\frac{\alpha }{{{\alpha }_{o}}}\approx \frac{\tan \alpha }{\tan {{\alpha }_{o}}}\)              (1)

Với a là góc trông ảnh cho bởi \(\tan \alpha =\frac{{{A}_{2}}{{B}_{2}}}{\left| d_{2}^{/} \right|}\)        (2)

a₀ là góc trông Mặt Trăng bằng mắt không qua kính, cho bởi \(\tan {{\alpha }_{0}}=\frac{{{A}_{1}}{{B}_{1}}}{{{O}_{1}}{{A}_{1}}}=\frac{{{A}_{1}}{{B}_{1}}}{{{f}_{1}}}\)        (3)

+ Từ (1), (2) và (3) ta có : \({{G}_{v}}=\frac{{{A}_{2}}{{B}_{2}}}{\left| d_{2}^{/} \right|}.\frac{{{f}_{1}}}{{{A}_{1}}{{B}_{1}}}\)

\(\Rightarrow {{G}_{v}}=\frac{{{A}_{2}}{{B}_{2}}}{{{A}_{1}}{{B}_{1}}}.\frac{{{f}_{1}}}{\left| d_{2}^{/} \right|}=\left| \frac{d_{2}^{/}}{{{d}_{2}}} \right|.\frac{{{f}_{1}}}{\left| d_{2}^{/} \right|}=\frac{{{f}_{1}}}{{{d}_{2}}}=\frac{120}{3,7}\approx 32,4\)

Ví dụ 3: Một kính thiên văn khúc xạ được điều chỉnh cho một người có mắt bình thường nhìn được ảnh rõ nét của một vật ở vô cực mà không phải điều tiết. Khi đó khoảng cách giữa vật kính và thị kính là 62 cm và số bội giác của kính là G = 30.

a) Xác định tiêu cực của vật khính và thị kính.

b) Vật quan sát Mặt Trăng có góc trông \({{\alpha }_{0}}=\frac{1}{100}\left( rad \right)\). Tính đường kính của Mặt Trăng cho bởi vật kính.

Hướng dẫn giải

a) Quá trình tạo ảnh của kính thiên văn giống như quá trình tạo ảnh qua hệ hai thấu kính ghép đồng trục và được tóm tắt qua sơ đồ sau: \(AB\xrightarrow{{{L}_{1}}}{{A}_{1}}{{B}_{1}}\xrightarrow{{{L}_{2}}}{{A}_{2}}{{B}_{2}}\)

+ Vì quan sát Mặt Trăng ở rất xa nên \({{d}_{1}}=\infty \Rightarrow d_{1}^{/}={{f}_{1}}\)

+ Vì ngắm chứng ở vô cực nên \(d_{2}^{/}=\infty \Rightarrow {{d}_{2}}={{f}_{2}}\)

+ Gọi a là khoảng cách giữa hai kính, ta có:

\(a=d_{1}^{/}+{{d}_{2}}={{f}_{1}}+{{f}_{2}}=62\)      (1)

+ Số bộ giác của kính thiên văn khi ngắm chừng ở vô cực:

\({{G}_{\infty }}=\frac{{{f}_{1}}}{{{f}_{2}}}=30\)                               (2)

+ Từ (1) và (2) suy ra f₁ = 60 cm và f₂ = 2 cm

 b) Mặt Trăng là vật AB ở xa vô cực → d₁ = \(\infty \), qua vật kính cho ảnh A₁B₁ ở ngay tiêu điểm ảnh \(F_{1}^{/}\Rightarrow d_{1}^{/}={{f}_{1}}\)

+ Từ hình vẽ suy ra đường kính của Mặt Trăng cho bởi vật kính là:

\(\tan {{\alpha }_{0}}=\frac{{{A}_{1}}{{B}_{1}}}{{{f}_{1}}}\Rightarrow {{A}_{1}}{{B}_{1}}={{f}_{1}}\tan {{\alpha }_{0}}\approx {{f}_{1}}{{\alpha }_{0}}=\frac{60}{100}=0,6\left( cm \right)\)

Bài 1. Vật kính của một kính thiên văn dùng ở trường học có tiêu cự f₁ = 120 cm. Thị kính là một thấu kính hội tụ có tiêu cự f₂ = 4 cm. Tính khoảng cách giữa hai kính và số bội giác của kính thiên văn khi ngắm chừng ở vô cực.

Bài 2. Vật kính của một kính thiên văn là một thấu kính hội tụ có tiêu cự lớn, thị kính là một thấu kính hội tụ có tiêu cự nhỏ. Một người, mắt không có tật, dùng kính thiên văn này để quan sát Mặt Trăng ở trạng thái không điều tiết. Khi đó khoảng cách giữa vật kính và thị kính là 90 cm. Số bội giác của kính là 17. Tính tiêu cự của vật kính và thị kính. Coi mắt đặt sát kính.

Bài 3. Một kính thiên văn có vật kính với độ tụ 0,5 điôp. Thị kính cho phép nhìn một vật cao 1 mm đặt tại tiêu diện vật dưới một góc là j = 0,05 rad.

a. Tìm tiêu cự của thị kính.

b. Tính số bội giác của kính thiên văn lúc ngắm chừng ở vô cực.

c. Tính khoảng cách giữa hai điểm trên Mặt Trăng, nếu góc trông hai điểm này nhìn qua kính là 4^/. Coi khoảng cách từ Trái Đất đến Mặt Trăng là 400000 km.

Bài 4. Vật kính của một kính thiên văn học sinh có tiêu cự f₁ = 1,2m. Thị kính là một thấu kính hội tụ có tiêu cự f₂ = 4cm.

a)  Tính khoảng cách giữa hai kính và độ bội giác của kính thiên văn khi ngắm chừng ở vô cực.

b)  Một học sinh dùng kính thiên văn nói trên để quan sát Mặt Trăng. Điểm cực viễn của học sinh này cách mắt 50cm. Tính khoảng cách giữa hai kính và độ bội giác của kính khi học sinh đó quan sát không điều tiết.

-----( Để xem đầy đủ nội dung của tài liệu, các em vui lòng xem Online hoặc Đăng nhập để tải về máy)------

Trên đây là trích dẫn một phần nội dung tài liệu Phương pháp giải bài tập về kính thiên văn môn Vật Lý 11 năm 2021-2022. Để xem thêm nhiều tư liệu hữu ích khác, các em đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.

Hy vọng tài liệu này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong học tập.

Ngoài ra các em có thể tham khảo thêm một số tư liệu cùng chuyên mục sau:

• Phương pháp giải dạng bài tập về phản xạ toàn phần môn Vật Lý 11 năm 2021-2022
• Phương pháp giải bài tập chuyên đề lăng kính môn Vật Lý 11 năm 2021-2022