DŲ░ß╗øi ─æ├óy l├Ā HŲ░ß╗øng dß║½n giß║Żi b├Āi tß║Łp To├Īn 11 n├óng cao ChŲ░ŲĪng 4 Luyß╗ćn tß║Łp (trang 143) ─æŲ░ß╗Żc hoc247 bi├¬n soß║Īn v├Ā tß╗Ģng hß╗Żp, nß╗Öi dung b├Īm s├Īt theo chŲ░ŲĪng tr├¼nh SGK Giß║Żi t├Łch 11 n├óng cao gi├║p c├Īc em hß╗Źc sinh nß║»m vß╗»ng phŲ░ŲĪng ph├Īp giß║Żi b├Āi tß║Łp v├Ā ├┤n tß║Łp kiß║┐n thß╗®c hiß╗ću quß║Ż hŲĪn.
B├Āi 16 trang 143 SGK To├Īn 11 n├óng cao
T├¼m c├Īc giß╗øi hß║Īn sau:
a) \(\lim \frac{{{n^2} + 4n - 5}}{{3{n^3} + {n^2} - 7}}\)
b) \(\lim \frac{{{n^5} + {n^4} - 3n - 2}}{{4{n^3} + 6{n^2} + 9}}\)
c) \(\lim \frac{{\sqrt {2{n^4} + 3n - 2} }}{{2{n^2} - n + 3}}\)
d) \(\lim \frac{{{3^n} - {{2.5}^n}}}{{7 + {{3.5}^n}}}\)
HŲ░ß╗øng dß║½n giß║Żi:
Câu a:
\(\lim \frac{{{n^2} + 4n - 5}}{{3{n^3} + {n^2} - 7}} = \lim \frac{{{n^3}\left( {\frac{1}{n} + \frac{4}{{{n^2}}} - \frac{5}{{{n^3}}}} \right)}}{{{n^3}\left( {3 + \frac{1}{n} + \frac{7}{{{n^3}}}} \right)}} = \lim \frac{{\frac{1}{n} + \frac{4}{{{n^2}}} - \frac{5}{{{n^3}}}}}{{3 + \frac{1}{n} + \frac{7}{{{n^3}}}}} = \frac{0}{3} = 0\)
Câu b:
\(\begin{array}{*{20}{l}}
{\lim \frac{{{n^5} + {n^4} - 3n - 2}}{{4{n^3} + 6{n^2} + 9}} = \lim {n^2}.\frac{{{n^3}\left( {1 + \frac{1}{n} - \frac{3}{{{n^4}}} - \frac{2}{{{n^5}}}} \right)}}{{{n^3}\left( {4 + \frac{6}{n} + \frac{9}{{{n^3}}}} \right)}}}\\
{ = \lim {n^2}.\frac{{\left( {1 + \frac{1}{n} - \frac{3}{{{n^4}}} - \frac{2}{{{n^5}}}} \right)}}{{\left( {4 + \frac{6}{n} + \frac{9}{{{n^3}}}} \right)}} = + \infty }
\end{array}\)
Câu c:
\(\begin{array}{l}
\lim \frac{{\sqrt {2{n^4} + 3n - 2} }}{{2{n^2} - n + 3}} = \lim \frac{{{n^2}\sqrt {2 + \frac{3}{{{n^3}}} - \frac{2}{{{n^4}}}} }}{{{n^2}\left( {2 - \frac{1}{n} + \frac{3}{{{n^2}}}} \right)}}\\
= \lim \frac{{\sqrt {2 + \frac{3}{{{n^3}}} - \frac{2}{{{n^4}}}} }}{{2 - \frac{1}{n} + \frac{3}{{{n^2}}}}} = \frac{{\sqrt 2 }}{2}
\end{array}\)
Câu d:
\(\lim \frac{{{3^n} - {{2.5}^n}}}{{7 + {{3.5}^n}}} = \lim \frac{{{{\left( {\frac{3}{5}} \right)}^n} - 2}}{{7.{{\left( {\frac{1}{5}} \right)}^n} + 3}} = - \frac{2}{3}\) (vì \(\lim {\left( {\frac{3}{5}} \right)^n} = \lim {\left( {\frac{1}{5}} \right)^n} = 0\))
B├Āi 17 trang 143 SGK To├Īn 11 n├óng cao
T├¼m c├Īc giß╗øi hß║Īn sau:
a) \(\lim \left( {3{n^3} - 7n + 11} \right)\)
b) \(\lim \sqrt {2{n^4} - {n^2} + n + 2} \)
c) \(\lim \sqrt[3]{{1 + 2n - {n^3}}}\)
d) \(\lim \sqrt {{{2.3}^n} - n + 2} \)
HŲ░ß╗øng dß║½n giß║Żi:
Câu a:
\(\lim \left( {3{n^3} - 7n + 11} \right) = \lim {n^3}\left( {3 - \frac{7}{{{n^2}}} + \frac{{11}}{{{n^3}}}} \right) = + \infty \)
(vì \(\lim {n^3} = + \infty ,\lim \left( {3 - \frac{7}{{{n^2}}} + \frac{{11}}{{{n^3}}}} \right) = 3 > 0\))
Câu b:
\(\lim \sqrt {2{n^4} - {n^2} + n + 2} = \lim {n^2}.\sqrt {2 - \frac{1}{{{n^2}}} + \frac{1}{{{n^3}}} + \frac{2}{{{n^4}}}} = + \infty \)
(vì \(\lim {n^2} = + \infty ,\lim \sqrt {2 - \frac{1}{{{n^2}}} + \frac{1}{{{n^3}}} + \frac{2}{{{n^4}}}} = \sqrt 2 > 0\))
Câu c:
\(\lim \sqrt[3]{{1 + 2n - {n^3}}} = \lim n.\sqrt[3]{{\frac{1}{{{n^3}}} + \frac{2}{{{n^2}}} - 1}} = - \infty \)
(vì \(\lim n = + \infty ,\lim \sqrt[3]{{\frac{1}{{{n^3}}} + \frac{2}{{{n^2}}} - 1}} = - 1 < 0\))
Câu d:
Ta c├│ \(\sqrt {{{2.3}^n} - n + 2} = {\left( {\sqrt 3 } \right)^n}.\sqrt {2 - \frac{n}{{{3^n}}} + \frac{2}{{{3^n}}}} \) vß╗øi mß╗Źi n.
V├¼ \(\lim \frac{n}{{{3^n}}} = 0\) (kß║┐t quß║Ż b├Āi 4) v├Ā \(\lim \frac{2}{{{3^n}}} = 0\) n├¬n \(\lim \sqrt {2 - \frac{n}{{{3^n}}} + \frac{2}{{{3^n}}}} = \sqrt 2 > 0\)
Ngo├Āi ra \(\lim {\left( {\sqrt 3 } \right)^n} = + \infty \)
Do đó \(\lim \sqrt {{{2.3}^n} - n + 2} = + \infty \).
B├Āi 18 trang 143 SGK To├Īn 11 n├óng cao
T├¼m c├Īc giß╗øi hß║Īn sau:
a) \(\lim \left( {\sqrt {{n^2} + n + 1} - n} \right)\)
HŲ░ß╗øng dß║½n: Nh├ón v├Ā chia biß╗āu thß╗®c ─æ├Ż cho vß╗øi \({\sqrt {{n^2} + n + 1} + n}\)
b) \(\lim \frac{1}{{\sqrt {n + 2} - \sqrt {n + 1} }}\)
HŲ░ß╗øng dß║½n: Nh├ón tß╗Ł v├Ā mß║½u cß╗¦a ph├ón thß╗®c ─æ├Ż cho vß╗øi \({\sqrt {n + 2} + \sqrt {n + 1} }\)
c) \(\lim {\rm{ }}\left( {\sqrt {{n^2} + n + 2} - \sqrt {n + 1} } \right)\)
d) \(\lim \frac{1}{{\sqrt {3n + 2} - \sqrt {2n + 1} }}\)
e) \(\lim \left( {\sqrt {n + 1} - \sqrt n } \right)n\)
f) \(\lim \frac{{\sqrt {{n^2} + 1} - \sqrt {n + 1} }}{{3n + 2}}\)
HŲ░ß╗øng dß║½n giß║Żi:
Câu a:
\(\begin{array}{l}
\lim \left( {\sqrt {{n^2} + n + 1} - n} \right) = \lim \frac{{\left( {{n^2} + n + 1} \right) - {n^2}}}{{\sqrt {{n^2} + n + 1} + n}}\\
= \lim \frac{{n + 1}}{{\sqrt {{n^2} + n + 1} + n}} = \lim \frac{{n\left( {1 + \frac{1}{n}} \right)}}{{n\left( {\sqrt {1 + \frac{1}{n} + \frac{1}{{{n^2}}}} + 1} \right)}}\\
= \lim \frac{{1 + \frac{1}{n}}}{{\sqrt {1 + \frac{1}{n} + \frac{1}{{{n^2}}}} + 1}} = \frac{1}{2}
\end{array}\)
Câu b:
\(\lim \frac{1}{{\sqrt {n + 2} - \sqrt {n + 1} }} = \lim \frac{{\sqrt {n + 2} + \sqrt {n + 1} }}{{n + 2 - n - 1}} = \lim \left( {\sqrt {n + 2} + \sqrt {n + 1} } \right) = + \infty \)
Câu c:
\(\begin{array}{l}
\lim \left( {\sqrt {{n^2} + n + 2} - \sqrt {n + 1} } \right) = \lim n.\left( {\sqrt {1 + \frac{1}{n} + \frac{2}{{{n^2}}}} - \sqrt {\frac{1}{n} + \frac{1}{{{n^2}}}} } \right) = + \infty \\
=
\end{array}\)
(vì \(\begin{array}{l}
\lim n = + \infty ,\lim \left( {\sqrt {1 + \frac{1}{n} + \frac{2}{{{n^2}}}} - \sqrt {\frac{1}{n} + \frac{1}{{{n^2}}}} } \right) = 1 > 0\\
=
\end{array}\))
Câu d:
\(\begin{array}{l}
\lim \frac{1}{{\sqrt {3n + 2} - \sqrt {2n + 1} }} = \lim \frac{{\sqrt {3n + 2} + \sqrt {2n + 1} }}{{3n + 2 - 2n - 1}}\\
= \lim \frac{{\sqrt {3n + 2} + \sqrt {2n + 1} }}{{n + 1}} = \lim \frac{{n\left( {\sqrt {\frac{3}{n} + \frac{2}{{{n^2}}}} + \sqrt {\frac{2}{n} + \frac{1}{{{n^2}}}} } \right)}}{{n\left( {1 + \frac{1}{n}} \right)}}\\
= \lim \frac{{\sqrt {\frac{3}{n} + \frac{2}{{{n^2}}}} + \sqrt {\frac{2}{n} + \frac{1}{{{n^2}}}} }}{{1 + \frac{1}{n}}} = 0
\end{array}\)
Câu e:
\(\lim \left( {\sqrt {n + 1} - \sqrt n } \right)n = \lim \sqrt n .\frac{{\sqrt n }}{{\sqrt {n + 1} + \sqrt n }} = \lim \sqrt n .\frac{1}{{\sqrt {1 + \frac{1}{n}} + 1}} = + \infty \)
(vì \(\lim \sqrt n = + \infty ,lim\frac{1}{{\sqrt {1 + \frac{1}{n}} + 1}} = \frac{1}{2} > 0\))
Câu f:
\(\begin{array}{l}
\lim \frac{{\sqrt {{n^2} + 1} - \sqrt {n + 1} }}{{3n + 2}} = \lim \frac{{n\left( {\sqrt {1 + \frac{1}{{{n^2}}}} - \sqrt {\frac{1}{n} + \frac{1}{{{n^2}}}} } \right)}}{{n\left( {3 + \frac{2}{n}} \right)}}\\
= \lim \frac{{\sqrt {1 + \frac{1}{{{n^2}}}} - \sqrt {\frac{1}{n} + \frac{1}{{{n^2}}}} }}{{3 + \frac{2}{n}}} = \frac{1}{3}
\end{array}\)
B├Āi 19 trang 143 SGK To├Īn 11 n├óng cao
Tß╗Ģng cß╗¦a mß╗Öt cß║źp sß╗æ nh├ón l├╣i v├┤ hß║Īn l├Ā \(\frac{5}{3}\), tß╗Ģng ba sß╗æ hß║Īng ─æß║¦u ti├¬n cß╗¦a n├│ l├Ā \(\frac{{39}}{{25}}\). T├¼m sß╗æ hß║Īng ─æß║¦u v├Ā c├┤ng bß╗Öi cß╗¦a cß║źp sß╗æ ─æ├│.
HŲ░ß╗øng dß║½n giß║Żi:
Ta c├│:
\(\begin{array}{l}
S = \frac{{{u_1}}}{{1 - q}} = \frac{5}{3}\,\,\,\,\,\left( 1 \right)\\
{u_1} + {u_2} + {u_3} = {u_1}\left( {1 + q + {q^2}} \right) = \frac{{39}}{{25}}\\
\Rightarrow \frac{{{u_1}}}{{1 - q}}\left( {1 - {q^3}} \right) = \frac{{39}}{{25}}\,\,\,\,\left( 2 \right)
\end{array}\)
Thay (1) v├Āo (2) ta ─æŲ░ß╗Żc: \(\frac{5}{3}\left( {1 - {q^3}} \right) = \frac{{39}}{{25}} \Rightarrow q = \frac{2}{5}\)
Từ (1) suy ra u1 = 1.
Vß║Ły \({u_1} = 1,q = \frac{2}{5}\).
B├Āi 20 trang 143 SGK To├Īn 11 n├óng cao
Bông tuyết Vôn Kốc
Ta bß║»t ─æß║¦u tß╗½ mß╗Öt tam gi├Īc ─æß╗üu cß║Īnh a. Chia mß╗Śi cß║Īnh cß╗¦a tam gi├Īc ABC th├Ānh ba ─æoß║Īn thß║│ng bß║▒ng nhau. Tr├¬n mß╗Śi ─æoß║Īn thß║│ng ß╗¤ giß╗»a, dß╗▒ng mß╗Öt tam gi├Īc ─æß╗üu nß║▒m ngo├Āi tam gi├Īc ABC rß╗ōi x├│a ─æ├Īy cß╗¦a n├│, ta ─æŲ░ß╗Żc ─æŲ░ß╗Øng gß║źp kh├║c kh├®p k├Łn H1. Chia mß╗Śi cß║Īnh H1 th├Ānh ba ─æoß║Īn thß║│ng bß║▒ng nhau. Tr├¬n mß╗Śi ─æoß║Īn thß║│ng ß╗¤ giß╗»a, dß╗▒ng mß╗Öt tam gi├Īc ─æß╗üu nß║▒m ngo├Āi H1 rß╗ōi x├│a ─æ├Īy cß╗¦a n├│, ta ─æŲ░ß╗Żc ─æŲ░ß╗Øng gß║źp kh├║c kh├®p k├Łn H2. Tiß║┐p tß╗źc nhŲ░ vß║Ły, ta ─æŲ░ß╗Żc mß╗Öt h├¼nh giß╗æng nhŲ░ b├┤ng tuyß║┐t, gß╗Źi l├Ā b├┤ng tuyß║┐t V├┤n Kß╗æc (h. 4.6).
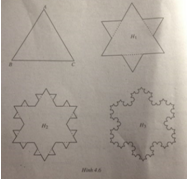
a. Gß╗Źi p1, p2,ŌĆ”, pn,ŌĆ” l├Ā ─æß╗Ö d├Āi cß╗¦a H1, H2,ŌĆ”, Hn,ŌĆ” . Chß╗®ng minh rß║▒ng (pn) l├Ā mß╗Öt cß║źp sß╗æ nh├ón. T├¼m \(\lim p_n\).
b. Gß╗Źi Sn l├Ā diß╗ćn t├Łch cß╗¦a miß╗ün giß╗øi hß║Īn bß╗¤i ─æŲ░ß╗Øng gß║źp kh├║c Hn. T├Łnh Sn v├Ā t├¼m giß╗øi hß║Īn cß╗¦a d├Ży sß╗æ (Sn).
HŲ░ß╗øng dß║½n: Sß╗æ cß║Īnh cß╗¦a Hn l├Ā 3.4n. T├¼m ─æß╗Ö d├Āi mß╗Śi cß║Īnh cß╗¦a Hn, tß╗½ ─æ├│ t├Łnh pn. ─Éß╗ā t├Łnh Sn cß║¦n ch├║ ├Į rß║▒ng muß╗æn c├│ Hn+1 chß╗ē cß║¦n th├¬m v├Āo mß╗Öt tam gi├Īc ─æß╗üu nhß╗Å tr├¬n mß╗Śi cß║Īnh cß╗¦a Hn.
HŲ░ß╗øng dß║½n giß║Żi:
Câu a:
Sß╗æ cß║Īnh cß╗¦a Hn l├Ā 3.4n.
─Éß╗Ö d├Āi mß╗Śi cß║Īnh cß╗¦a Hn l├Ā \(\frac{a}{{{3^n}}}\)
Do ─æ├│ ─æß╗Ö d├Āi cß╗¦a H┬Ł┬Łn l├Ā \({p_n} = {3.4^n}.\frac{a}{{{3^n}}} = 3a{\left( {\frac{4}{3}} \right)^n}\)
Vß║Ły d├Ży sß╗æ (pn) l├Ā mß╗Öt cß║źp sß╗æ nh├ón v├Ā \(\lim {p_n} = + \infty \)
Câu b:
Diß╗ćn t├Łch tam gi├Īc ABC cß║Īnh a l├Ā \(S = \frac{{{a^2}\sqrt 3 }}{4}\)
\(\begin{array}{l}
{S_1} - S = 3.\left( {\frac{S}{9}} \right) = \frac{S}{3}\\
{S_2} - {S_1} = 4.3.\left( {\frac{S}{{{9^2}}}} \right) = \frac{S}{3}.\left( {\frac{4}{9}} \right)\\
{S_3} - {S_2} = {4^2}.3.\left( {\frac{S}{{{9^3}}}} \right) = \frac{S}{3}.{\left( {\frac{4}{9}} \right)^2}
\end{array}\)
Bß║▒ng phŲ░ŲĪng ph├Īp qui nß║Īp, ta ─æŲ░ß╗Żc :
\({S_n} = {S_{n - 1}} = {4^{n - 1}}.3.\left( {\frac{S}{{{9^n}}}} \right) = \frac{S}{3}.{\left( {\frac{4}{9}} \right)^{n - 1}}\)
Cß╗Öng tß╗½ng vß║┐ n ─æß║│ng thß╗®c tr├¬n, ta ─æŲ░ß╗Żc:
\({S_n} - S = \frac{S}{3} + \frac{S}{3}.\left( {\frac{4}{9}} \right) + \frac{S}{3}.{\left( {\frac{4}{9}} \right)^2} + ... + \frac{S}{3}.{\left( {\frac{4}{9}} \right)^{n - 1}}\,\,\,\left( 1 \right)\)
Vß║┐ phß║Żi cß╗¦a (1) l├Ā tß╗Ģng cß╗¦a n sß╗æ hß║Īng ─æß║¦u ti├¬n cß╗¦a cß║źp sß╗æ nh├ón l├╣i v├┤ hß║Īn c├│ sß╗æ hß║Īng ─æß║¦u l├Ā \(\frac{S}{3}\)v├Ā c├┤ng bß╗Öi l├Ā \({\frac{4}{9}}\). Tß╗Ģng cß╗¦a cß║źp sß╗æ nh├ón n├Āy l├Ā:
\(\left( {\frac{S}{3}} \right).\frac{1}{{1 - \frac{4}{9}}} = \frac{{3S}}{5}\)
Do đó \(\lim \left( {{S_n} - S} \right) = \frac{{3S}}{5}\)
Suy ra \(\lim {S_n} = \frac{{3S}}{5} + S = \frac{{8S}}{5} = \frac{8}{5}.\frac{{{a^2}\sqrt 3 }}{4} = \frac{{2\sqrt 3 }}{5}{a^2}\)
Tr├¬n ─æ├óy l├Ā nß╗Öi dung chi tiß║┐t Giß║Żi b├Āi tß║Łp n├óng cao To├Īn 11 ChŲ░ŲĪng 4 Luyß╗ćn tß║Łp (trang 143) vß╗øi hŲ░ß╗øng dß║½n giß║Żi chi tiß║┐t, r├Ą r├Āng, tr├¼nh b├Āy khoa hß╗Źc. Hoc247 hy vß╗Źng ─æ├óy sß║Į l├Ā t├Āi liß╗ću hß╗»u ├Łch gi├║p c├Īc bß║Īn hß╗Źc sinh lß╗øp 11 hß╗Źc tß║Łp thß║Łt tß╗æt.
TŲ░ liß╗ću nß╗Ģi bß║Łt tuß║¦n
- Xem thêm







