Giải Toán 11 SGK nâng cao Chương 1 Luyện tập (trang 31, 32)

Tìm tập xác định của mỗi hàm số sau:

a) \(y = \frac{{1 - \cos x}}{{2\sin x + \sqrt 2 }}\)

b) \(y = \frac{{\sin \left( {x - 2} \right)}}{{\cos 2x - \cos x}}\)

c) \(y = \frac{{\tan x}}{{1 + \tan x}}\)

d) \(y = \frac{1}{{\sqrt 3 \cot 2x + 1}}\)

Hướng dẫn giải:

Câu a:

\(y = \frac{{1 - \cos x}}{{2\sin x + \sqrt 2 }}\) xác định \( \Leftrightarrow 2\sin x + \sqrt 2  \ne 0\)

\( \Leftrightarrow {\mathop{\rm sinx}\nolimits}  \ne  - \frac{{\sqrt 2 }}{2} \Leftrightarrow \left\{ \begin{array}{l}
x \ne  - \frac{\pi }{4} + k2\pi \\
x \ne \frac{{5\pi }}{4} + k2\pi 
\end{array} \right.\)

Vậy \(D = R\backslash \left( {\left\{ { - \frac{\pi }{4} + k2\pi ,k \in Z} \right\} \cup \left\{ {\frac{{5\pi }}{4} + k2\pi ,k \in Z} \right\}} \right)\)

Câu b:

\(y = \frac{{\sin \left( {x - 2} \right)}}{{\cos 2x - \cos x}}\) xác định \( \Leftrightarrow \cos 2x \ne \cos x\)

\( \Leftrightarrow \left\{ \begin{array}{l}
2x \ne x + k2\pi \\
2x \ne  - x + k2\pi 
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x \ne k2\pi \\
x \ne k\frac{{2\pi }}{3}
\end{array} \right. \Leftrightarrow x \ne k\frac{{2\pi }}{3}\)

Vậy \(D = R\backslash \left\{ {k\frac{{2\pi }}{3},k \in Z} \right\}\)

Câu c:

\(y = \frac{{\tan x}}{{1 + \tan x}}\) xác định \( \Leftrightarrow \tan x \ne  - 1 \Leftrightarrow \left\{ \begin{array}{l}
x \ne \frac{\pi }{2} + k\pi \\
x \ne  - \frac{\pi }{4} + k\pi 
\end{array} \right.\)

Vậy \(D = R\backslash \left( {\left\{ {\frac{\pi }{2} + k\pi ,k \in Z} \right\} \cup \left\{ { - \frac{\pi }{4} + k\pi ,k \in Z} \right\}} \right)\)

Câu d:

\(y = \frac{1}{{\sqrt 3 \cot 2x + 1}}\) xác định \( \Leftrightarrow \cot 2x \ne  - \frac{1}{{\sqrt 3 }}\)

\( \Leftrightarrow \left\{ \begin{array}{l}
2x \ne k\pi \\
2x \ne  - \frac{\pi }{3} + k\pi 
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x \ne k\frac{\pi }{2}\\
x \ne  - \frac{\pi }{6} + k\frac{\pi }{2}
\end{array} \right.\)

Vậy \(D = R\backslash \left( {\left\{ {k\frac{\pi }{2},k \in Z} \right\} \cup \left\{ { - \frac{\pi }{6} + k\frac{\pi }{2},k \in Z} \right\}} \right)\)

---

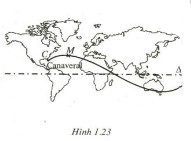
Giả sử một con tàu vũ trụ được phóng lên từ mũi Ca-na-vơ-ran (Canaveral) ở Mĩ. Nó chuyển động theo một quỹ đạo được mô tả trên một bản đồ phẳng (quanh đường xích đạo) của mặt đất

như hình 1.23: điểm M mô tả cho con tàu, đường thẳng Δ mô tả cho đường xích đạo.

Khoảng cách h (kilomet) từ M đến Δ được tính theo công thức h = |d|, trong đó:

\(d = 400\cos \left[ {\frac{\pi }{{45}}\left( {t - 10} \right)} \right]\)

Với t (phút) là thời gian trôi qua kể từ khi con tàu đi vào quỹ đạo, d > 0 nếu M ở phía trên Δ, d < 0 nếu M ở phía dưới Δ.

a. Giả thiết rằng con tàu đi vào quỹ đạo ngay từ khi phóng lên tại mũi Ca-na-vơ-ran (tức là ứng với t = 0). Hãy tính khoảng cách từ điểm C đến đường thẳng Δ, trong đó C là điểm trên bản đồ biểu diễn cho mũi Ca-na-vơ-ran.

b. Tìm thời điểm sớm nhất sau khi con tàu đi vào quỹ đạo để có d = 2000.

c. Tìm thời điểm sớm nhất sau khi con tàu đi vào quỹ đạo để có d = −1236.

(Tính chính xác các kết quả đến hàng phần nghìn).

Hướng dẫn giải:

Câu a:

Vì t = 0 nên \(d = 4000\cos \left( { - \frac{{10\pi }}{{45}}} \right) = 400\cos \frac{{2\pi }}{9}\). Do đó:

\(h = \left| d \right| \approx 3064,178\left( {km} \right)\)

Câu b:

\(\begin{array}{l}
d = 2000 \Leftrightarrow 400\cos \left[ {\frac{\pi }{{45}}\left( {t - 10} \right)} \right] = 2000 \Leftrightarrow \cos \left[ {\frac{\pi }{{45}}\left( {t - 10} \right)} \right] = \frac{1}{2}\\
 \Leftrightarrow \frac{\pi }{{45}}\left( {t - 10} \right) =  \pm \frac{\pi }{3} + k2\pi \\
 \Leftrightarrow t = 10 \pm 15 + 90k\\
 \Leftrightarrow \left[ \begin{array}{l}
t = 25 + 90k\\
t =  - 5 + 90k
\end{array} \right.
\end{array}\)

Chú ý rằng t > 0 ta thấy ngay giá trị nhỏ nhất của t là t = 25. Vậy d = 2000 (km) xảy ra lần đầu tiên sau khi phóng con tàu vào quỹ đạo được 25 phút.

Câu c:

\(\begin{array}{l}
d =  - 1236 \Leftrightarrow 400\cos \left[ {\frac{\pi }{{45}}\left( {t - 10} \right)} \right] =  - 1236 \Leftrightarrow \cos \left[ {\frac{\pi }{{45}}\left( {t - 10} \right)} \right] =  - 0,309\\
 \Leftrightarrow \frac{\pi }{{45}}\left( {t - 10} \right) =  \pm \alpha  + k2\pi \left( {k \in Z,cos\alpha  =  - 0,309} \right)\\
 \Leftrightarrow t =  \pm \frac{{45}}{\pi }\alpha  + 10 + 90k
\end{array}\)

Sử dụng bảng số hoặc máy tính bỏ túi, ta có thể chọn \(\alpha  \approx 1,885\). Khi đó ta có:

\(t \approx  \pm 27,000 + 10 + 90k\), tức là \(t \approx  - 17,000 + 90k\) hoặc \(t \approx 37,000 + 90k\)

Dễ thấy giá trị dương nhỏ nhất của tt là 37,000. Vậy d = −1236 (km) xảy ra lần đầu tiên là 37,000 phút sau khi con tàu được phóng vào quỹ đạo. 

---

Một chiếc guồng nước có dạng hình tròn bán kính 2,5m; trục của nó đặt cách mặt nước 2m (h.1.24). Khi guồng quay đều, khoảng cách h (mét) từ một chiếc gầu gắn tại điểm A của guồng đến mặt nước được tính theo công thức h = |y|, trong đó

\(y = 2 + 2,5\sin \left[ {2\pi \left( {x - \frac{1}{4}} \right)} \right]\)

Với x là thời gian quay guồng (x ≥ 0), tính bằng phút ; ta quy ước rằng y > 0 khi gầu ở bên trên mặt nước và y < 0 khi gầu ở dưới nước (xem bài đọc thêm về dao động điều hòa trang 15). Hỏi :

a. Khi nào thì chiếc gầu ở vị trí thấp nhất ?

b. Khi nào thì chiếc gầu ở vị trí cao nhất ?

c. Chiếc gầu cách mặt nước 2m lần đầu tiên khi nào ?

Hướng dẫn giải:

Câu a:

Chiếc gầu ở vị trí thấp nhất khi \(\sin \left[ {2\pi \left( {x - \frac{1}{4}} \right)} \right] =  - 1\). Ta có:

\(\begin{array}{l}
y = 2 + 2,5\sin \left[ {2\pi \left( {x - \frac{1}{4}} \right)} \right]\\
\sin \left[ {2\pi \left( {x - \frac{1}{4}} \right)} \right] =  - 1 \Leftrightarrow 2\pi \left( {x - \frac{1}{4}} \right) =  - \frac{\pi }{2} + k2\pi \\
 \Leftrightarrow x = k\left( {k \in N} \right)
\end{array}\)

Điều đó chứng tỏ rằng chiếc gầu ở vị trí thấp nhất tại các thời điểm 0 phút ; 1 phút ; 2 phút ; 3 phút…

Câu b:

Chiếc gầu ở vị trí cao nhất khi \(\sin \left[ {2\pi \left( {x - \frac{1}{4}} \right)} \right] = 1\). Ta có:

\(\begin{array}{l}
y = 2 + 2,5\sin \left[ {2\pi \left( {x - \frac{1}{4}} \right)} \right]\\
\sin \left[ {2\pi \left( {x - \frac{1}{4}} \right)} \right] = 1 \Leftrightarrow 2\pi \left( {x - \frac{1}{4}} \right) = \frac{\pi }{2} + k2\pi \\
 \Leftrightarrow x = \frac{1}{2} + k\left( {k \in N} \right)
\end{array}\)

Điều đó chứng tỏ chiếc gàu ở vị trí cao nhất tại các thời điểm 0,5 phút; 1,5 phút ; 2,5 phút ; 3,5 phút …

Câu c:

Chiếc gàu cách mặt nước 2 mét khi \(\sin \left[ {2\pi \left( {x - \frac{1}{4}} \right)} \right] = 0\), nghĩa là tại các thời điểm \(x = \frac{1}{4} + \frac{1}{2}k\) (phút); do đó lần đầu tiên nó cách mặt nước 2 mét khi quay được \(\frac{1}{4}\) phút (ứng với k = 0). 

---

Dùng công thức biến đổi tổng thành tích , giải các phương trình sau:

a) \(\cos 3x = \sin 2x\)

b) \(\sin \left( {x - {{120}^0}} \right) - \cos 2x = 0\)

Hướng dẫn giải:

Câu a:

\(\begin{array}{l}
\cos 3x = \sin 2x \Leftrightarrow \cos 3x - \cos \left( {\frac{\pi }{2} - 2x} \right) = 0\\
 \Leftrightarrow  - 2\sin \left( {\frac{x}{2} + \frac{\pi }{4}} \right)\sin \left( {\frac{{5x}}{2} - \frac{\pi }{4}} \right) = 0\\
 \Leftrightarrow \left[ \begin{array}{l}
\frac{x}{2} + \frac{\pi }{4} = k\pi \\
\frac{{5x}}{2} - \frac{\pi }{4} = k\pi 
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
x =  - \frac{\pi }{2} + k2\pi \\
x = \frac{\pi }{{10}} + k\frac{{2\pi }}{5}
\end{array} \right.
\end{array}\)

Câu b:

\(\begin{array}{l}
\sin \left( {x - {{120}^0}} \right) - \cos 2x = 0 \Leftrightarrow \cos \left( {{{210}^0} - x} \right) - \cos 2x = 0\\
 \Leftrightarrow  - 2\sin \left( {\frac{x}{2} + {{105}^0}} \right)\sin \left( {{{105}^0} - \frac{{3x}}{2}} \right) = 0\\
 \Leftrightarrow \left[ \begin{array}{l}
\frac{x}{2} + {105^0} = k{180^0}\\
{105^0} - \frac{{3x}}{2} = k{180^0}
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
x =  - {210^0} + k{360^0}\\
x = {70^0} + k{120^0}
\end{array} \right.
\end{array}\)

 

Trên đây là nội dung chi tiết Giải bài tập nâng cao Toán 11 Chương 1 Luyện tập (trang 31, 32) với hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. Hoc247 hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 11 học tập thật tốt.