Khám phá 3 trang 45 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST

Trên một tờ giấy kẻ caro có các đường kẻ ngang song song và cách đều nhau.

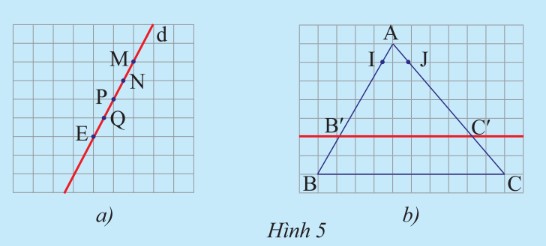
a) Vẽ một đường thẳng $d$ cắt các đường kẻ ngang của tờ giấy như trong Hình 5a. Hãy so sánh độ dài các đoạn thẳng $MN, NP, PQ$ và $QE$?

b) Vẽ một tam giác $ABC$ rồi vẽ một đường thẳng song song với cạnh $BC$ và cắt hai cạnh $AB, AC$ lần lượt tại $B'$ và $C'$. Trên cạnh $AB$, lấy đoạn $AI$ làm đơn vị đo tính tỉ số $AB'$ và $B'B$; trên cạnh $AC$, lấy đoạn $AJ$ làm đơn vị đo tính tỉ số $AC'$ và $C'C$ (Hình 5b)?

So sánh các tỉ số $\frac{AB'}{AB}$ và $\frac{AC'}{AC};\frac{AB'}{B'B}$ và $\frac{AC'}{C'C};\frac{B'B}{AB}$ và $\frac{C'C}{AC}$?