Bài tập 8 trang 51 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST

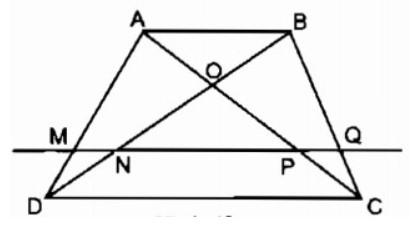
Trong tam giác ADB, ta có: $MN // AB$ (gt)

Suy ra: $\frac{DN}{DB}=\frac{MN}{AB}$ (Hệ quả định lí Thales )   (1)

Trong tam giác ACB, ta có: $PQ // AB$ (gt)

Suy ra: $\frac{CQ}{CB}=\frac{PQ}{AB}$ (Hệ quả định lí Thales )  (2)

Lại có:

$NQ // AB$ (gt)

$AB // CD$ (gt)

Suy ra: $NQ // CD$

Trong tam giác BDC, ta có: $NQ // CD$ (chứng minh trên)

Suy ra: $\frac{DN}{DB}=\frac{CQ}{CB}$ (Định lí Thales )  (3)

Từ (1), (2) và (3) suy ra: $\frac{MN}{AB}=\frac{PQ}{AB}$ hay $MN = PQ$.

-- Mod Toán 8 HỌC247