Phần hướng dẫn giải bài tập Toán 8 Chân trời sáng tạo Chương 8 Bài 3 Các trường hợp đồng dạng của hai tam giác vuông sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng, giải bài tập từ SGK Toán 8 Tập 2 Chân trời sáng tạo.
-
Khởi động trang 73 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bóng của một ngọn cờ trên mặt đất dài \(6~m\). Cùng thời điểm đó một thanh sắt cao \(2,4~m\) cắm vuông góc với mặt đất có bóng dài \(1,8~m\). Tính chiều cao của cột cờ?
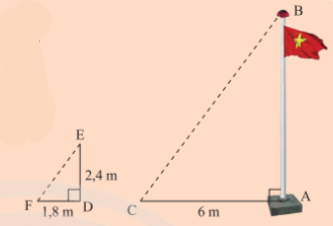
-
Khám phá 1 trang 73 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
a) Từ trường hợp đồng dạng thứ ba của hai tam giác, xét xem tam giác ABC vuông tại A và tam giác MNP vuông tại M có \(\widehat{B}=\widehat{N}\) thì hai tam giác đó có đồng dạng với nhau không?
b) Từ trường hợp đồng dạng thứ hai của hai tam giác, xét xem nếu tam giác ABC vuông tại A và tam giác MNP vuông tại M có \(\frac{AB}{MN}=\frac{AC}{MP}\) thì tam giác đó có đồng dạng với nhau không?
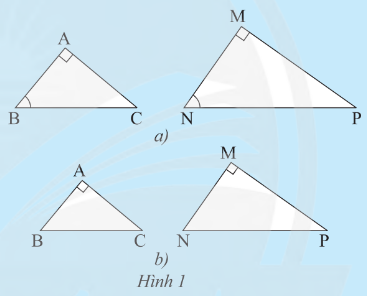
-
Thực hành 1 trang 74 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Cho tam giác DEF vuông tại D có DH là đường cao (Hình 3). Chứng minh rằng \(DE^{2}=EH.EF\)?
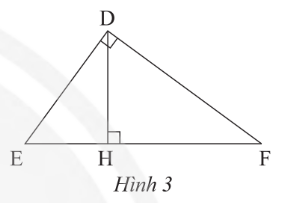
-
Vận dụng 1 trang 74 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Tính chiều cao của cột cờ trong phần Khởi động (trang 73)?
-
Khám phá 2 trang 74 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Cho hai tam giác vuông ABC và DEF có các kích thước như Hình 4.
a) Hãy tính độ dài cạnh AC và DF?
b) So sánh các tỉ số \(\frac{AB}{DE},\frac{AC}{DF}\) và \(\frac{BC}{EF}\)?
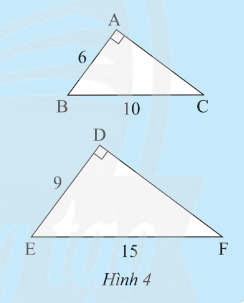
-
Thực hành 2 trang 75 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
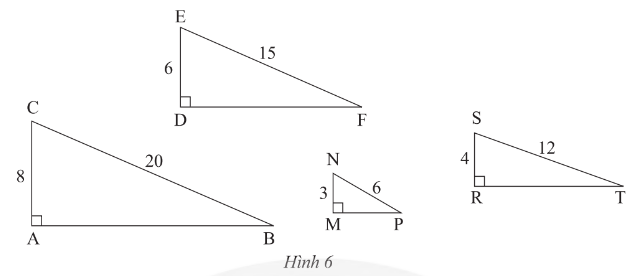
Trong Hình 6, tam giác nào đồng dạng với tam giác \(DEF\)?
-
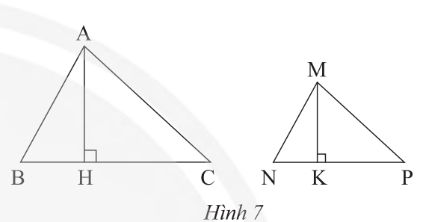
Vận dụng 2 trang 75 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Trong Hình 7, biết \(\Delta MNP~ᔕ~\Delta ABC\) với tỉ số đồng dạng \(k=\frac{MN}{AB}\), hai đường cao tương ứng là MK và AH.
a) Chứng minh rằng \(\Delta MNK~ᔕ~\Delta ABH\) và \(\frac{MK}{AH}=k\)?
b) Gọi \(S_{1}\) là diện tích tam giác MNP và \(S_{2}\) là diện tích tam giác ABC. Chứng minh rằng \(\frac{S_{1}}{S_{2}}=k^{2}\)?
-
Bài tập 1 trang 75 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
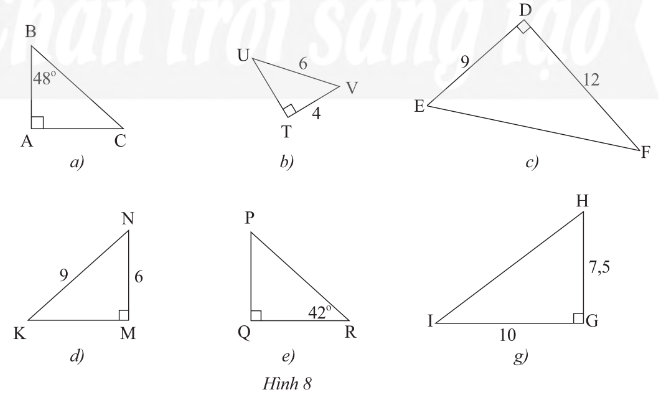
Hãy tìm cặp tam giác vuông đồng dạng trong Hình 8?
-
Bài tập 2 trang 76 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Quan sát hình 9
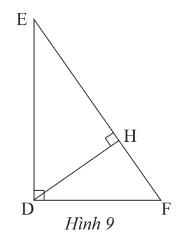
a) Chứng minh rằng \(\Delta DEF~ᔕ~\Delta HDF\)?
b) Chứng minh \(DF^{2}=FH.FE\)?
c) Biết EF = 15 cm, FH = 5,4 cm. Tính độ dài đoạn thẳng DF?
-
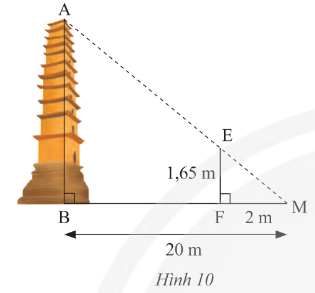
Bài tập 3 trang 76 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Trong Hình 10, biết MB = 20m, MF = 2m, EF = 1,65 m. Tính chiều cao AB của ngọn tháp?
-
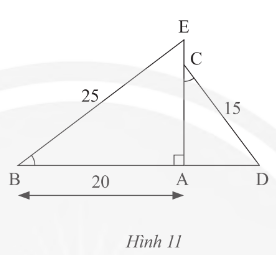
Bài tập 4 trang 76 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Trong Hình 11, cho biết \(\widehat{B}=\widehat{C}\), BE = 25cm, AB = 20cm, DC = 15cm. Tính độ dài đoạn thẳng CE?
-
Bài tập 5 trang 76 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Quan sát Hình 12. Chứng minh rằng:
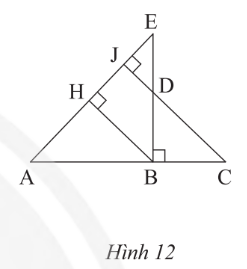
a) \(\Delta ABH~ᔕ~\Delta DCB\)?
b) \(\frac{BC}{BE}=\frac{BD}{BA}\)?
-
Bài tập 6 trang 76 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Một người đo chiều cao của một tòa nhà nhờ một cọc chôn xuống đất, cọc cao 3m và đặt cách xa tòa nhà 27 m. Sau khi người ấy lùi ra xa cách cọc 1,2 m thì nhìn thấy đầu cọc và đỉnh tòa nhà cùng nằm trên một đường thẳng. Hỏi tòa nhà cao bao nhiêu mét, biết rằng khoảng cách từ chân đến mắt người ấy là 1,5m?
-
Bài tập 7 trang 76 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Cho tam giác ABC vuông tại A có đường cao AH. Kẻ HM vuông góc với AB tại M.
a) Chứng minh rằng ΔAMH ᔕ ΔAHB?
b) Kẻ HN vuông góc với AC tại N. Chứng minh rằng AM.AB = AN.AC?
c) Chứng minh rằng ΔANM ᔕ ΔABC?
d) Cho biết AB = 9cm, AC = 12 cm. Tính diện tích tam giác AMH?






