Giải bài 27 tr 10 sách BT Toán lớp 8 Tập 2
Dùng máy tính bỏ túi để tính giá trị gần đúng các nghiệm của mỗi phương trình sau, làm tròn đến chữ số thập phân thứ ba.
a. \(\left( {\sqrt 3 - x\sqrt 5 } \right)\left( {2x\sqrt 2 + 1} \right) = 0\)
b. \(\left( {2x - \sqrt 7 } \right)\left( {x\sqrt {10} + 3} \right) = 0\)
c. \(\left( {2 - 3x\sqrt 5 } \right)\left( {2,5x + \sqrt 2 } \right) = 0\)
d. \(\left( {\sqrt {13} + 5x} \right)\left( {3,4 - 4x\sqrt {1,7} } \right) = 0\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Áp dụng phương pháp giải phương trình tích :
\( A(x).B(x) = 0 ⇔ A(x) = 0\) hoặc \(B(x) = 0.\)
Lời giải chi tiết
a. \(\left( {\sqrt 3 - x\sqrt 5 } \right)\left( {2x\sqrt 2 + 1} \right) = 0 \Leftrightarrow \sqrt 3 - x\sqrt 5 = 0\) hoặc \(2x\sqrt 2 + 1 = 0\)
+ \(\sqrt 3 - x\sqrt 5 = 0 \Leftrightarrow x = {{\sqrt 3 } \over {\sqrt 5 }} \approx 0,775\)
+ \(2x\sqrt 2 + 1 = 0 \Leftrightarrow x = - {1 \over {2\sqrt 2 }} \approx - 0,354\)
Phương trình có nghiệm x = 0,775 hoặc x = -0,354
b. \(\left( {2x - \sqrt 7 } \right)\left( {x\sqrt {10} + 3} \right) = 0 \Leftrightarrow 2x - \sqrt 7 = 0\) hoặc \(x\sqrt {10} + 3 = 0\)
+ \(2x - \sqrt 7 = 0 \Leftrightarrow x = {{\sqrt 7 } \over 2} \approx 1,323\)
+ \(x\sqrt {10} + 3 = 0 \Leftrightarrow x = - {3 \over {\sqrt {10} }} \approx - 0,949\)
Phương trình có nghiệm x = 1,323 hoặc x = -0,949
c. \(\left( {2 - 3x\sqrt 5 } \right)\left( {2,5x + \sqrt 2 } \right) = \) \( \Leftrightarrow 2 - 3x\sqrt 5 = 0\) hoặc \(2,5x + \sqrt 2 = 0\)
+ \(2 - 3x\sqrt 5 = 0 \Leftrightarrow x = {2 \over {3\sqrt 5 }} \approx 0,298\)
+ \(2,5x + \sqrt 2 = 0 \Leftrightarrow x = {{ - \sqrt 2 } \over {2,5}} \approx - 0,566\)
Phương trình có nghiệm x = 0,298 hoặc x = -0,566
d. \(\left( {\sqrt {13} + 5x} \right)\left( {3,4 - 4x\sqrt {1,7} } \right) = 0\)
\( \Leftrightarrow \sqrt {13} + 5x = 0\) Hoặc \(3,4 - 4x\sqrt {1,7} = 0\)
+ \(\sqrt {13} + 5x = 0 \Leftrightarrow x = - {{\sqrt {13} } \over 5} \approx - 0,721\)
+ \(3,4 - 4x\sqrt {1,7} = 0\) \( \Leftrightarrow x = {{3,4} \over {4\sqrt {1,7} }} \approx 0,652\)
Phương trình có nghiệm x = -0,721 hoặc x = 0,652
-- Mod Toán 8 HỌC247
-


Giải phương trình \({x^3} - {x^2} = 1 - x\)
bởi Lê Gia Bảo
 27/05/2020
Theo dõi (0) 2 Trả lời
27/05/2020
Theo dõi (0) 2 Trả lời -

 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Nêu cách giải phương trình tích
bởi Trần Bảo Việt
 27/05/2020
Theo dõi (0) 1 Trả lời
27/05/2020
Theo dõi (0) 1 Trả lời -


Giải phương trình (frac{{x - 3}}{{2014}} + frac{{x - 2}}{{2015}} - = frac{{x - 1}}{{1008}} + frac{x}{{2017}} - 1)
bởi Đinh T. Hoàng
 26/05/2020
Theo dõi (0) 0 Trả lời
26/05/2020
Theo dõi (0) 0 Trả lời -

 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Giải phương trình (x^2+x)(x^2+x+1)=6
bởi Nhungoc
 17/05/2020
17/05/2020
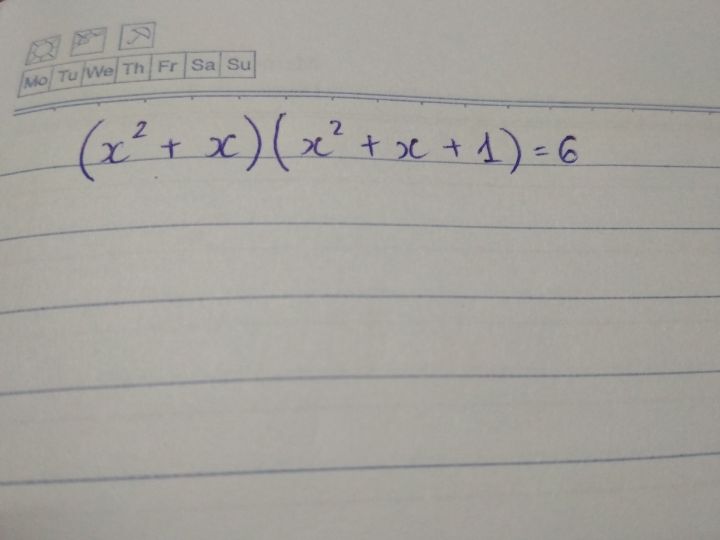 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải phương trình (x^2-4x)^2+2(x-2)^2=43
bởi Phương Linh
 13/05/2020
Giúp mình với ạ:(( Mình cần gấp bây giờ ạ:((
13/05/2020
Giúp mình với ạ:(( Mình cần gấp bây giờ ạ:((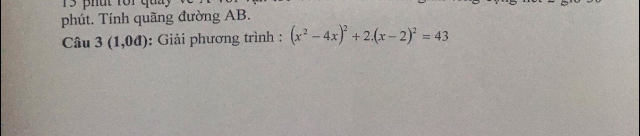 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tìm x biết (2x+5)^2 =(3x-1)^2
bởi Ro Agama
 06/05/2020
06/05/2020
(2x+5)^2 =(3x-1)^2
Theo dõi (0) 8 Trả lời -


Giải phương trình (2x+1)(x-1)=0
bởi Tta Đàoo
 03/05/2020
X/2(x-3) x/2(x 1)=2x/(x 1)(x-3)
03/05/2020
X/2(x-3) x/2(x 1)=2x/(x 1)(x-3)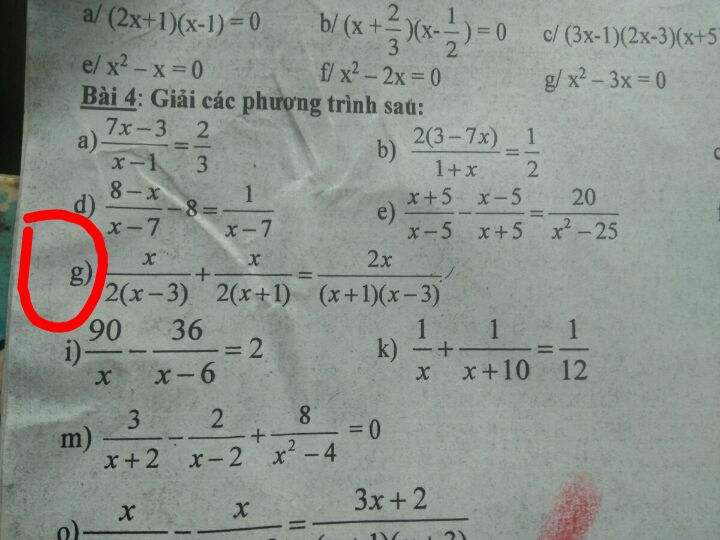 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -


Giải phương trình (x-1).(x² +3x-2)(x³-1)=0
bởi Chi Nguyễn
 30/04/2020
30/04/2020
Giải phương trình (x-1).(x² 3x-2)(x³-1)=0
Theo dõi (0) 1 Trả lời -


Giải phương trình 2x-3=4x-7
bởi Nguyễn Hùng
 30/04/2020
Giải phương trình2x-3=4x-7Theo dõi (0) 4 Trả lời
30/04/2020
Giải phương trình2x-3=4x-7Theo dõi (0) 4 Trả lời -


Giải phương trình (2x+1)(x^2+2)=0
bởi Trần Lê Phương
 25/04/2020
25/04/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải phương trình x^3+3x^2+3x-1=0
bởi Mai Hồ Hồng
 24/04/2020
24/04/2020
Giải phương trình x^3+3x^2+3x-1=0
Theo dõi (0) 3 Trả lời -


Tìm x biết (x+3)^4 (x+5)^4=2
bởi Nek Trời Ơi Ly
 23/04/2020
Mọi ng làm tiếp giúp em ạ
23/04/2020
Mọi ng làm tiếp giúp em ạ Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Giải phương trình (3x-2)/(x+7)=(6x+1)/(2x-3)
bởi Thanh Mac
 23/04/2020
Giúp e với ạ
23/04/2020
Giúp e với ạ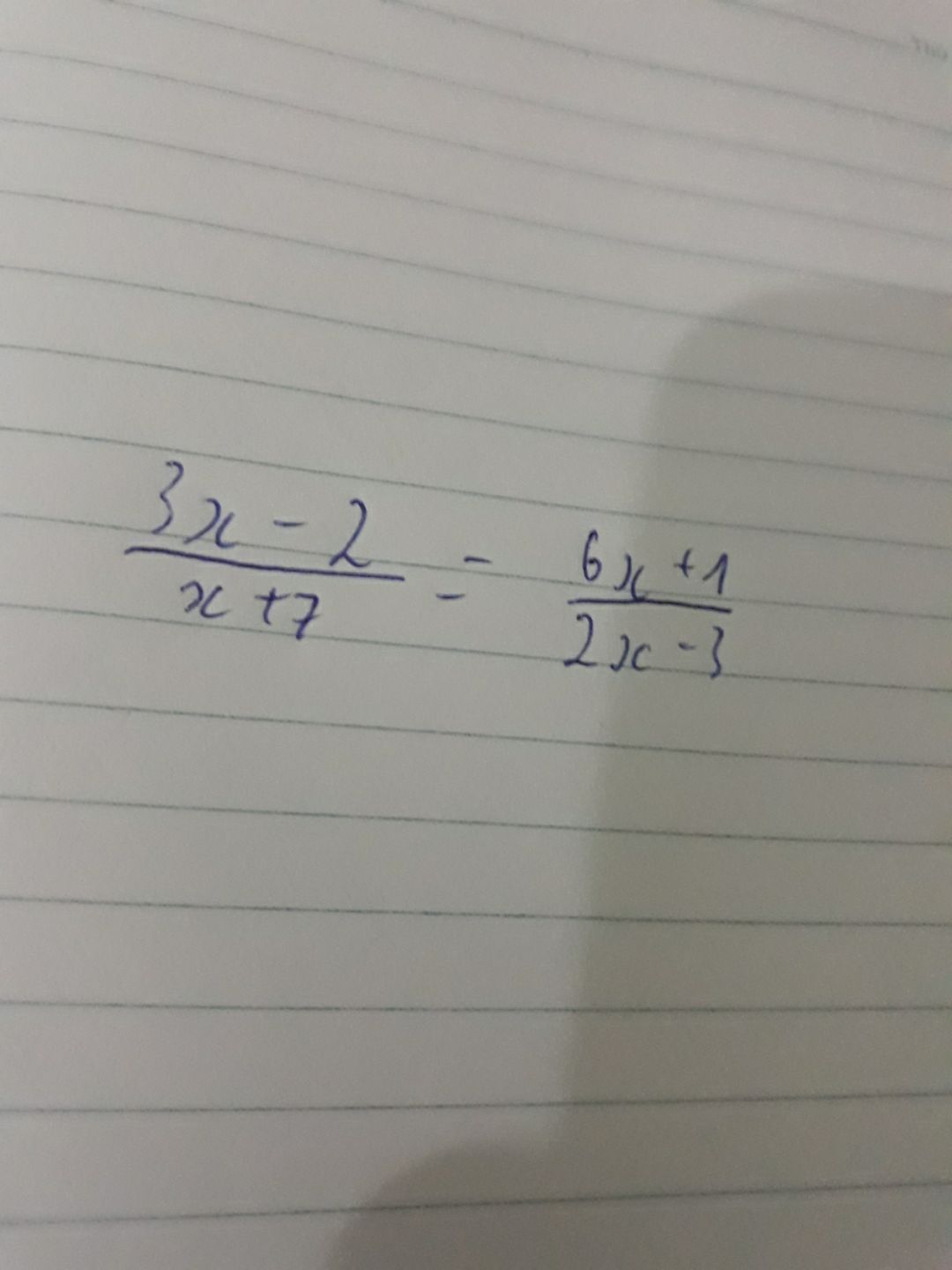 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Giải phương trình x^3-3x^2+3x-1=(x-1)(x+1)
bởi Lee Min Ho
 21/04/2020
21/04/2020
Giải phương trình x^3-3x^2+3x-1=(x-1)(x+1)
Theo dõi (1) 3 Trả lời -


Giải phương trình 3x+9=2x-5
bởi CT
 20/04/2020
20/04/2020
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


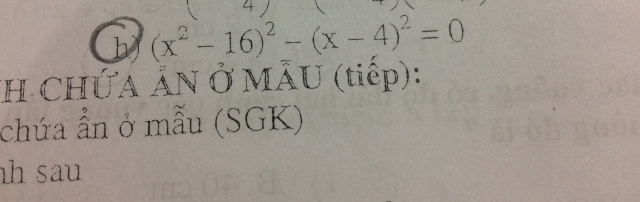 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -


Giải phương trình (x+2)(x+4)(x+6)(x+8) +16=0
bởi Nguyễn Lan Anh
 19/04/2020
19/04/2020
Giải phương trình (x+2)(x+4)(x+6)(x+8) +16=0
Theo dõi (0) 1 Trả lời -


 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Giải phương trình 4x-12=0
bởi Hoàng Thương
 15/04/2020
15/04/2020
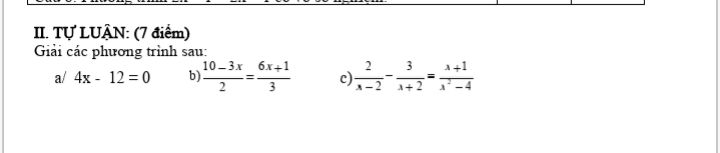 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Giải phương trình x+3/x-4=x-1/x-2
bởi Vuong Tran
 15/04/2020
15/04/2020
Giải phương trình x+3/x-4=x-1/x-2
Theo dõi (0) 2 Trả lời -


Giải phương trình x(x-2)^2 + (x+2)(x-2)=0
bởi Phúc Quang Đào
 14/04/2020
14/04/2020
x(x-2)2 + (x+2)(x-2)=0
Theo dõi (0) 3 Trả lời -


Giải phương trình (3x-5)^2-(x-1)^2=0
bởi Chời Ơi Chủ Nè
 13/04/2020
Giải giúp mình vớiTheo dõi (0) 0 Trả lời
13/04/2020
Giải giúp mình vớiTheo dõi (0) 0 Trả lời -


Tìm tập nghiệm của phương trình (2x+1)(3x-2)=0
bởi Nhỏ's Thín's
 12/04/2020
Tap nghiem phuong trinh
12/04/2020
Tap nghiem phuong trinh Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Giải phương trình (x^2-1)(x 2)(x-3)=(x-1)(x^2-4)(x 5)
bởi Đỗ Thuận
 10/04/2020
10/04/2020
Giải phương trình (x^2-1)(x 2)(x-3)=(x-1)(x^2-4)(x 5)
Theo dõi (0) 0 Trả lời -


Giải phương trình (3x-2)(4x+5)=0
bởi Bắp Ngô
 07/04/2020
Giải các phương trình
07/04/2020
Giải các phương trình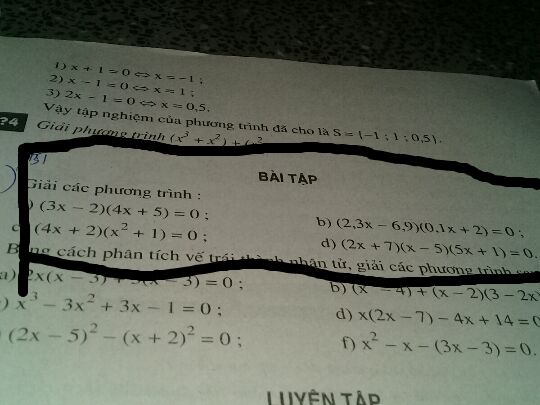 Theo dõi (1) 3 Trả lời
Theo dõi (1) 3 Trả lời -


Giải phương trình 3x-5=3+2x
bởi Bùi Thị Thùy Ngân
 07/04/2020
Giúp
07/04/2020
Giúp Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Giải phương trình (x-2)(3x 5)=(x-4)(x+1)
bởi Thien Nguyen
 07/04/2020
07/04/2020
Giải phương trình (x-2)(3x 5)=(x-4)(x+1)
Theo dõi (0) 0 Trả lời -


Giải phương trình (2x-3)(x+1)=0
bởi Nguyễn Mai Anh
 02/04/2020
02/04/2020
 Theo dõi (1) 12 Trả lời
Theo dõi (1) 12 Trả lời -


Giải phương trình x^2-3x 2=0
bởi Danh Thị Kim Lý
 31/03/2020
31/03/2020
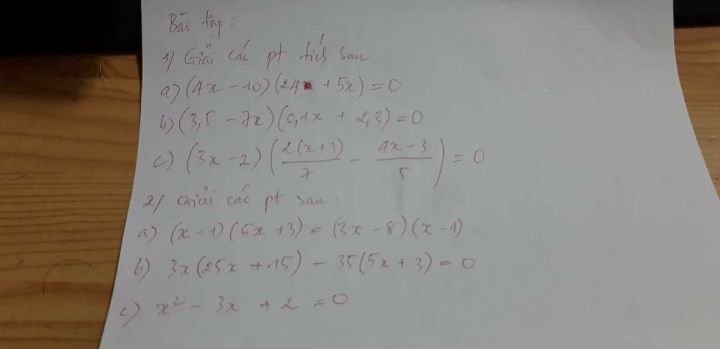 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Giải phương trình (2x-1)^2+(2-x)(2x-1)=0
bởi Vũ Ngọc Như
 31/03/2020
Phương trình tích
31/03/2020
Phương trình tích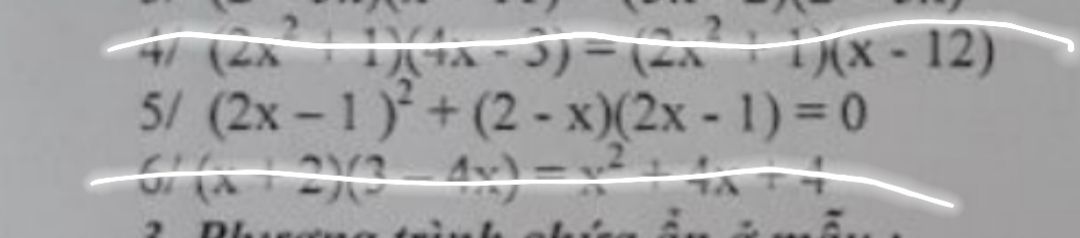 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Giải phương trình (x+2)/327+(x+3)/326+(x+4)/325+(x+5)/324+(x+349)/5=0
bởi Tuyet Nhi Nguyen Hoan
 27/03/2020
27/03/2020
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Giải phương trình 1+x/(3-x)=5x/(x+2)(x-3)+2/(x+2)
bởi Hồ Nguyên
 26/03/2020
Giải giùm mik với
26/03/2020
Giải giùm mik với Theo dõi (0) 6 Trả lời
Theo dõi (0) 6 Trả lời






