Giải bài 9.35 trang 83 SGK Toán 7 Kết nối tri thức tập 2
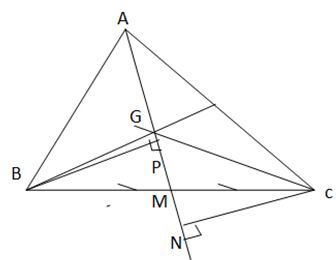
Kí hiệu S(ABC) là diện tích tam giác ABC. Gọi G là trọng tâm tam giác ABC, M là trung điểm BC
a) Chúng minh S(GBC) = \(\frac{1}{3}\) S(ABC)
Gợi ý: sử dụng GM= \(\frac{1}{3}\) AM để chứng minh S(GMB) = \(\frac{1}{3}\)S(ABM) , S(GCM) = \(\frac{1}{3}\)S(ACM)
b) Chứng minh S(GCA) = S(GAB) = \(\frac{1}{3}\)S(ABC)
Hướng dẫn giải chi tiết Giải bài 9.35
Phương pháp giải
sử dụng GM= \(\frac{1}{3}\) AM để chứng minh S(GMB) = \(\frac{1}{3}\)S(ABM) , S(GCM) = \(\frac{1}{3}\)S(ACM)
Lời giải chi tiết
a) Vì G là trọng tâm tam giác ABC nên GM= \(\frac{1}{3}\) AM
Kẻ BP ⊥ AM ta có S (GMB)= \(\frac{1}{2}\) BP . GM.
S ( ABM) = \(\frac{1}{2}\) BP . AM.
Ta có S (GMB)= \(\frac{1}{2}\) BP . GM.
=> S (GMB)= \(\frac{1}{2}\) BP . \(\frac{1}{3}\) AM
=> S (GMB) = \(\frac{1}{3}\) AM. \(\frac{1}{2}\) BP
=> S (GMB)= \(\frac{1}{3}\) S (ABM) (1)
Tương tự, kẻ CN ⊥ AM, ta có S (GMC)= \(\frac{1}{2}\) CN . GM.
S ( ACM) = \(\frac{1}{2}\) CN . AM.
mà GM= \(\frac{1}{3}\) AM
=> S (GMC)= \(\frac{1}{3}\) S (ACM) (2)
Cộng 2 vế của (1) và (2) ta có:
S (GMB) + S (GMC)= \(\frac{1}{3}\) S (AMC) + \(\frac{1}{3}\) S (ABM)
=> S( GBC) = \(\frac{1}{3}\) S( ABC)
b) BP ⊥ AM => BP ⊥ AG
CN ⊥ AM => CN ⊥ AG
Ta có S (GAB)= \(\frac{1}{2}\) BP . AG.
S (GAC)= \(\frac{1}{2}\) CN . AG.
Xét ∆ BPM vuông tại P và ∆ CNM vuông tại N có:
BM= CM ( M là trung điểm của BC)
\(\widehat{PMB}\) = \(\widehat{CMN}\) ( 2 góc đối đỉnh)
=> ∆ BPM = ∆ CNM
=> BP = CN
=> S (GAB) = S (GAC)
Có AG= \(\frac{2}{3}\) AM
S (ACB) = S (GAB) + S (GAC) + S ( GCB)
=> S (ACB) = S (GAB) + S (GAC) + \(\frac{1}{3}\) S( ABC)
=> \(\frac{2}{3}\) S( ABC) = 2 S (GAC)
=> \(\frac{1}{3}\) S( ABC) = S (GAC) = S (GAB)
-- Mod Toán 7 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.