Giải bài 4.38 trang 87 SGK Toán 7 Kết nối tri thức tập 1
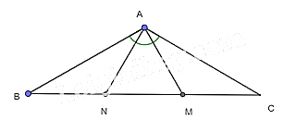
Cho tam giác ABC cân tại A có \(\widehat {A{\rm{ }}} = 120^\circ \). Trên cạnh BC lấy hai điểm M, N sao cho MA, NA lần lượt vuông góc với AB, AC. Chứng minh rằng:
a) \(\Delta \)BAM = \(\Delta \)CAN;
b) Các tam giác ANB, AMC lần lượt cân tại N, M.
Hướng dẫn giải chi tiết Giải bài 4.38
Phương pháp giải
a) Chứng minh 2 tam giác bằng nhau theo trường hợp g-c-g
b) Chứng minh tam giác có 2 cạnh bằng nhau hoặc 2 góc bằng nhau
Lời giải chi tiết
a) Xét 2 tam giác vuông BAM và CAN có:
AB=AC(Do tam giác ABC cân tại A)
\(\widehat B = \widehat C\) (Do tam giác ABC cân tại A)
=>\(\Delta BAM = \Delta CAN\)(g.c.g)
b)
Xét tam giác ABC cân tại A, có \(\widehat {A{\rm{ }}} = 120^\circ \) có:
\(\widehat B = \widehat C = \frac{{{{180}^o} - {{120}^o}}}{2} = {30^o}\).
Xét tam giác ABM vuông tại A có:
\(\begin{array}{l}\widehat B + \widehat {BAM} + \widehat {AMB} = {180^o}\\ \Rightarrow {30^o} + {90^o} + \widehat {AMB} = {180^o}\\ \Rightarrow \widehat {AMB} = {60^o}\\ \Rightarrow \widehat {AMC} = {180^o} - \widehat {AMB} = {180^o} - {60^o} = {120^o}\end{array}\)
Xét tam giác MAC có:
\(\begin{array}{l}\widehat {AMC} + \widehat {MAC} + \widehat C = {180^o}\\ \Rightarrow {120^o} + \widehat {MAC} + {30^o} = {180^o}\\ \Rightarrow \widehat {MAC} = {30^o} = \widehat C\end{array}\)
\(\Rightarrow \) Tam giác AMC cân tại M.
Vì \(\Delta BAM = \Delta CAN\)=>BM=CN => BN=MC
Xét 2 tam giác ANB và AMC có:
AB=AC
\(AN = AM\)(do \(\Delta BAM = \Delta CAN\))
BN=MC
=>\(\Delta ANB = \Delta AMC\)(c.c.c)
Mà tam giác AMC cân tại M.
=> Tam giác ANB cân tại N.
-- Mod Toán 7 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Giải bài 4.36 trang 87 SGK Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.37 trang 87 SGK Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.39 trang 87 SGK Toán 7 Kết nối tri thức tập 1 - KNTT
Giải Câu hỏi 1 trang 71 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải Câu hỏi 2 trang 71 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải Câu hỏi 3 trang 71 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải Câu hỏi 4 trang 71 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải Câu hỏi 5 trang 71 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải Câu hỏi 6 trang 72 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải Câu hỏi 7 trang 72 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.51 trang 72 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.52 trang 72 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.53 trang 72 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.54 trang 72 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.55 trang 73 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.56 trang 73 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.57 trang 73 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.58 trang 74 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.59 trang 74 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.60 trang 74 SBT Toán 7 Kết nối tri thức tập 1 - KNTT