Giải bài 3.30 trang 58 SGK Toán 7 Kết nối tri thức tập 1
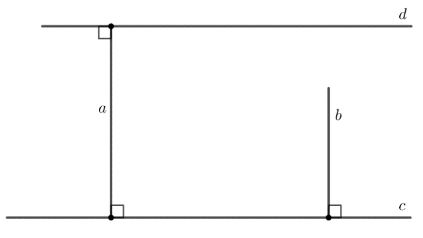
Cho hai đường thẳng phân biệt a, b cùng vuông góc với đường thẳng c; d là một đường thẳng khác c và d vuông góc với a. Chứng minh rằng:
a) a // b;
b) c // d;
c) b\( \bot \)d
Hướng dẫn giải chi tiết
Phương pháp giải
Định lí:
+) Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau
+) Đường thẳng vuông góc với 1 trong 2 đường thẳng song song thì cũng vuông góc với đường thẳng kia.
Lời giải chi tiết
a) Áp dụng định lí: “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau” ta có:
Do \(a \bot c,\,b \bot c\) nên a // b.
Vậy a // b.
b) Áp dụng định lí: “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau” ta có:
Do \(c \bot a,d \bot a\) nên c // d.
Vậy c // d.
c) Áp dụng định lí: “Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại” ta có:
Do \(b \bot c,\,c{\rm{\;//\;d}}\) nên \(b \bot {\rm{d}}.\)
Vậy \(b \bot {\rm{d}}.\)
-- Mod Toán 7 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.