Giải bài 1 trang 107 SGK Toán 7 Cánh diều tập 2
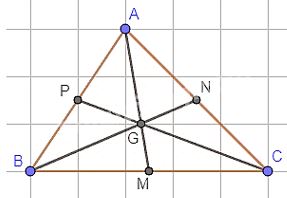
Cho tam giác ABC. Ba đường trung tuyến AM, BN, CP đồng quy tại G. Chứng minh: \(GA + GB + GC = \dfrac{2}{3}(AM + BN + CP)\).
Hướng dẫn giải chi tiết Bài 1
Phương pháp giải
Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng \(\dfrac{2}{3}\)độ dài đường trung tuyến đi qua đỉnh ấy.
Lời giải chi tiết
Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng \(\dfrac{2}{3}\)độ dài đường trung tuyến đi qua đỉnh ấy nên:
\(\begin{array}{l}\dfrac{{GA}}{{AM}} = \dfrac{{GB}}{{BN}} = \dfrac{{GC}}{{CP}} = \dfrac{2}{3}\\ \to GA = \dfrac{2}{3}AM;GB = \dfrac{2}{3}BN;GC = \dfrac{2}{3}CP\end{array}\)
Vậy:
\(GA + GB + GC = \dfrac{2}{3}AM + \dfrac{2}{3}BN + \dfrac{2}{3}CP = \dfrac{2}{3}(AM + BN + CP)\).
-- Mod Toán 7 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Luyện tập 2 trang 105 SGK Toán 7 Cánh diều tập 2 - CD
Hoạt động 3 trang 106 SGK Toán 7 Cánh diều tập 2 - CD
Giải bài 2 trang 107 SGK Toán 7 Cánh diều tập 2 - CD
Giải bài 3 trang 107 SGK Toán 7 Cánh diều tập 2 - CD
Giải bài 4 trang 107 SGK Toán 7 Cánh diều tập 2 - CD
Giải bài 5 trang 107 SGK Toán 7 Cánh diều tập 2 - CD
Giải bài 70 trang 89 SBT Toán 7 Cánh diều tập 2 - CD
Giải bài 71 trang 89 SBT Toán 7 Cánh diều tập 2 - CD
Giải bài 72 trang 90 SBT Toán 7 Cánh diều tập 2 - CD
Giải bài 73 trang 90 SBT Toán 7 Cánh diều tập 2 - CD
Giải bài 74 trang 90 SBT Toán 7 Cánh diều tập 2 - CD
Giải bài 75 trang 90 SBT Toán 7 Cánh diều tập 2 - CD
Giải bài 76 trang 90 SBT Toán 7 Cánh diều tập 2 - CD