Giải bài 72 trang 90 SBT Toán 7 Cánh diều tập 2 - CD

Phương pháp giải

Giả sử tam giác ABC có hai đường trung tuyến BM và CN bằng nhau chứng minh tam giác ABC cân tại A.

Lời giải chi tiết

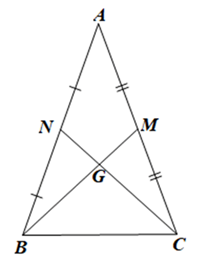
Tam giác ABC có hai trung tuyến BM và CN bằng nhau.

Gọi G là giao điểm của BM và CN.

Theo tính chất trọng tâm tam giác có: \(BG = \frac{2}{3}BM\)và \(CG = \frac{2}{3}CN\).

Vì BM = CN nên BG = CG.

Suy ra tam giác BGC cân tại G.

Do đó \(\widehat {GBC} = \widehat {GCB}\) (hai góc ở đáy).

Xét ∆MBC và ∆NCB có:

BC là cạnh chung,

\(\widehat {MBC} = \widehat {NCB}\) (do \(\widehat {GBC} = \widehat {GCB}\))

MB = NC (giả thiết)

Do đó ∆MBC = ∆NCB (c.g.c)

Suy ra \(\widehat {MCB} = \widehat {NBC}\) (hai góc tương ứng).

Khi đó tam giác ABC cân tại A.

Vậy nếu một tam giác có hai đường trung tuyến bằng nhau thì tam giác đó là tam giác cân.

-- Mod Toán 7 HỌC247