Toán 6 Cánh diều Bài 2: Tập hợp các số nguyên

- Số tự nhiên khác 0 còn được gọi là số nguyên dương

- Các số nguyên âm, số 0 và các số nguyên dương tạo thành tập hợp các số nguyên 

- Tập hợp các số nguyên được kí hiệu là Z

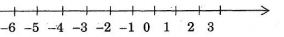
+ Trên trục số nằm ngang: Điểm \(0\)được gọi là điểm gốc của trục số. Chiều từ trái sang phải gọi là chiều dương (thường được đánh dấu bằng mũi tên), chiều từ phải sang trái gọi là chiều âm của trục số.

+ Trên trục số thẳng đứng, điểm biểu diễn số nguyên âm nằm dưới điểm 0, điểm biểu diễn số nguyên dương nằm trên điểm 0

+ Điểm biểu diễn số nguyên \(a\) trên trục số gọi là điểm \(a.\)

+) Cho số nguyên \(a\) và \(b\). Trên trục số, nếu điểm \(a\) nằm bên trái điểm \(b\) thì số \(a\) nhỏ hơn số \(b\), kí hiệu \(a < b\)

Ví dụ:

Số 2 trên trục số được gọi là điểm 2.

Số \( - 9\) trên trục số được gọi là điểm \( - 9\)

Ví dụ: Cho trục số như hình vẽ.

 

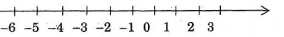
Ta thấy điểm biểu diễn số \( - 5\) nằm bên trái điểm biểu diễn số \( - 3\) nên \( - 5 <  - 3.\)

- Trên trục số, hai số nguyên(phân biệt) có điểm biểu diễn nằm về 2 phía của gốc 0 và cách đều gốc 0 được gọi là 2 số đối nhau

- Số đối của số 0 là 0

Cho số nguyên \(a\) và \(b\).

Trên trục số nằm ngang, nếu điểm \(a\) nằm bên trái điểm \(b\) thì số \(a\) nhỏ hơn số \(b\), kí hiệu \(a < b\)

Trên trục số thẳng đứng, nếu điểm \(a\) nằm bên dưới điểm \(b\) thì số \(a\) nhỏ hơn số \(b\), kí hiệu \(a < b\)

- Mọi số nguyên âm đều nhỏ hơn số nguyên dương.

- Để so sánh 2 số nguyên âm, ta làm 2 bước sau:

Bước 1: Bỏ dấu "-" trước cả 2 số âm 

Bước 2: Trong 2 số nguyên dương nhận được, số nào nhỏ hơn thì số nguyên âm ban đầu( trước khi bỏ dấu "-" lớn hơn

Chú ý:

- Mọi số nguyên âm đều nhỏ hơn 0.

- Mọi số nguyên dương đều lớn hơn 0.

- Nếu \(a,b\) là hai số nguyên dương và \(a > b\) thì \( - a <  - b\) (Thêm dấu “-” thì đổi dấu “>” thành dấu “<”)

- Nếu \(a,b\) là hai số nguyên dương và \(a < b\) thì \( - a >  - b\)

- Kí hiệu \(a \le b\) có nghĩa là “\(a < b\) hoặc \(a = b\)”

- Kí hiệu \(a \ge b\) có nghĩa là “\(a > b\) hoặc \(a = b\)”

Ví dụ:

5 là số nguyên dương và \( - 25\) là số nguyên âm nên \(5 >  - 25\)

Vì \(15 > 3\) nên \( - 15 <  - 3\)

Câu 1: Biểu diễn các số \( - 7, - 6, - 4,0,2,4\) trên một trục số.

Hướng dẫn giải

Gọi điểm biểu diễn các số \( - 7, - 6, - 4,0,2,4\) lần lượt là A, B, C, D, E.

Câu 2: Viết các số sau đây theo thứ tự tăng dần: \( - 6, - 12,40,0, - 18\).

Hướng dẫn giải

Số -18 nằm bên trái số -12 nên \( - 18 <  - 12\)

Số \( - 12\) nằm bên trái số \( - 6\) nên \( - 12 <  - 6\)

Số \( - 6\) là số nguyên âm nên \( - 6 < 0\)

Số 40 là số nguyên dương nên luôn lớn hơn 0=> \(0 < 40\)

=>Thứ tự tăng dần: - 18 < - 12 < - 6 < 0 < 40

Câu 3: Biểu diễn các số \( - 6\) và 4 trên trục số. Từ đó hãy so sánh \( - 6\) và 4.

Hướng dẫn giải

+Biểu diễn trên trục số:

+ So sánh \( - 6\) và 4:

Điểm \( - 6\) nằm bên trái số 0 nên \( - 6 < 0\). Số 4 nằm bên phải số 0 nên \(0 < 4\).

Từ đó ta có \( - 6 < 4\).

Qua bài giảng này giúp các em học được:

- Khái niệm số nguyên

- Giá trị tuyệt đối của số nguyên

- Vận dụng lý thuyết làm 1 số bài tập liên quan đến tập số nguyên

Câu 1: Quan sát trục số và trả lời các câu hỏi:

 

a) Điểm biểu diễn số 4 các điểm gốc 0 bao nhiêu đơn vị ?

b) Điểm biểu diễn số \( - 4\) cách điểm gốc 0 bao nhiêu đơn vị ?

c) Có nhận xét gì về khoảng cách từ điểm biểu diễn các số \( - 4\) và 4 đến điểm gốc 0?

Câu 2: Cho ví dụ về hai số nguyên đối nhau và hai số nguyên không đối nhau.

Câu 3: Viết các số sau theo thứ tự giảm dần: \( - 154, - 618, - 219,58\).

Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Toán 6 Cánh diều Chương 2 Bài 2 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.

• Câu 1:

  Xác định điểm cách -1 ba đơn vị theo chiều âm là:

  • A. 3
  • B. -3
  • C. -4
  • D. 4

• Câu 2:

  Trong các khẳng định sau, khẳng định nào đúng?

  • A. Nếu + 50 000 đồng biểu diễn số tiền có 50 000 đồng, thì – 50 000 đồng biểu diễn số tiền cho vay là 50 000 đồng.
  • B.  Số 0 là số nguyên dương.
  • C. Số đối của số 0 là số 0.
  • D. Số 0 là số nguyên âm.

• Câu 3:

  Cho tập hợp A = {-2; 0; 3; 6} . Tập hợp B gồm các phần tử là số đối của các phần tử trong tập hợp A là:

  • A. B = {-2; 0; -3; -6}
  • B. B = {2; 0; 3; 6}
  • C. B = {-6; -3; 0; 2}
  • D. B = {-2; 0; 3; 6}

Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!

Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Toán 6 Cánh diều Chương 2 Bài 2 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK Toán 6 tập 1

Hoạt động 1 trang 64 SGK Toán 6 Cánh diều tập 1 - CD

Luyện tập 1 trang 64 SGK Toán 6 Cánh diều tập 1 - CD

Hoạt động 2 trang 65 SGK Toán 6 Cánh diều tập 1 - CD

Luyện tập 2 trang 66 SGK Toán 6 Cánh diều tập 1 - CD

Hoạt động 3 trang 66 SGK Toán 6 Cánh diều tập 1 - CD

Luyện tập 3 trang 66 SGK Toán 6 Cánh diều tập 1 - CD

Hoạt động 4 trang 67 SGK Toán 6 Cánh diều tập 1 - CD

Luyện tập 4 trang 68 SGK Toán 6 Cánh diều tập 1 - CD

Hoạt động 5 trang 68 SGK Toán 6 Cánh diều tập 1 - CD

Hoạt động 6 trang 68 SGK Toán 6 Cánh diều tập 1 - CD

Luyện tập 5 trang 69 SGK Toán 6 Cánh diều tập 1 - CD

Giải bài 1 trang 69 SGK Toán 6 Cánh diều tập 1 - CD

Giải bài 2 trang 69 SGK Toán 6 Cánh diều tập 1 - CD

Giải bài 3 trang 69 SGK Toán 6 Cánh diều tập 1 - CD

Giải bài 4 trang 69 SGK Toán 6 Cánh diều tập 1 - CD

Giải bài 5 trang 69 SGK Toán 6 Cánh diều tập 1 - CD

Giải bài 6 trang 69 SGK Toán 6 Cánh diều tập 1 - CD

Giải bài 7 trang 69 SGK Toán 6 Cánh diều tập 1 - CD

Giải bài 8 trang 73 SBT Toán 6 Cánh diều tập 1 - CD

Giải bài 9 trang 73 SBT Toán 6 Cánh diều tập 1 - CD

Giải bài 10 trang 73 SBT Toán 6 Cánh diều tập 1 - CD

Giải bài 11 trang 73 SBT Toán 6 Cánh diều tập 1 - CD

Giải bài 12 trang 73 SBT Toán 6 Cánh diều tập 1 - CD

Giải bài 13 trang 73 SBT Toán 6 Cánh diều tập 1 - CD

Giải bài 14 trang 74 SBT Toán 6 Cánh diều tập 1 - CD

Giải bài 15 trang 74 SBT Toán 6 Cánh diều tập 1 - CD

Giải bài 16 trang 74 SBT Toán 6 Cánh diều tập 1 - CD

Giải bài 17 trang 74 SBT Toán 6 Cánh diều tập 1 - CD

Giải bài 18 trang 74 SBT Toán 6 Cánh diều tập 1 - CD

Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!

Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!