Giải bài tập Toán 11 Cánh Diều Chương 7 Bài 1: Định nghĩa đạo hàm. Ý nghĩa hình học của đạo hàm

Tính vận tốc tức thời của viên bi tại thời điểm \(x_{0}=1\)s trong bài toán tìm vận tốc tức thời?

Tính đạo hàm của hàm số \(f\left( x \right) = \frac{1}{x}\) tại \({x_0} = 2\) bằng định nghĩa?

Tính đạo hàm của hàm số \(f\left( x \right) = {x^3}\) tại điểm x bất kì bằng định nghĩa?

Cho hàm số y = f(x) có đồ thị (C), một điểm \({M_0}\) cố định thuộc (C) có hoành độ \({x_0}\). Với mỗi điểm M thuộc (C) khác \({M_0}\), kí hiệu \({x_M}\) là hoành độ của điểm M và \({k_M}\) là hệ số góc của cát tuyến \({M_0}M\). Giả sử tồn tại giới hạn hữu hạn \({k_0} = \mathop {\lim }\limits_{{x_M} \to {x_0}} {k_M}\). Khi đó, ta coi đường thẳng \({M_0}T\) đi qua \({M_0}\) và có hệ số góc là \({k_0}\) là ví trị giới hạn của cát tuyến \({M_0}M\) khi điểm M di chuyển dọc theo (C) dần tới \({M_0}\) . Đường thẳng \({M_0}T\)được gọi là tiếp tuyến của (C) tại điểm \({M_0}\), còn \({M_0}\) được gọi là tiếp điểm (Hình 3).

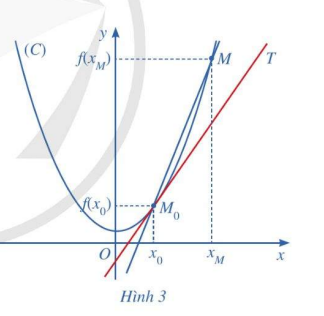
a) Xác định hệ số góc \({k_0}\) của tiếp tuyến \({M_0}T\) theo \({x_0}\)?

b) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm \({M_0}\)?

Viết phương trình tiếp tuyến của đồ thị hàm số \(y = \frac{1}{x}\) tại điểm N(1; 1)?

Tính đạo hàm của hàm số \(f(x) = 3{x^3} - 1\) tại điểm \({x_0} = 1\) bằng định nghĩa?

Chứng minh rằng hàm số \(f(x) = \left| x \right|\) không có đạo hàm tại điểm \({x_0} = 0\), nhưng có đạo hàm tại mọi điểm \(x \ne 0\)?

Cho hàm số \(y = - 2{x^2} + x\) có đồ thị (C).

a) Xác định hệ số góc của tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 2?

b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm M(2; - 6)?

Giả sử chi phí C (USD) để sản xuất Q máy vô tuyến là \(C(Q) = {Q^2} + 80Q + 3500\).

a) Ta gọi chi phí biên là chi phí gia tăng để sản xuất thêm 1 sản phẩm từ Q sản phẩm lên Q + 1 sản phẩm. Giả sử chi phí biên được xác định bởi hàm số C’(Q). Tìm hàm chi phí biên?

b) Tìm C’(90) và giải thích ý nghĩa kết quả tìm được?

c) Hãy tính chi phí sản xuất máy vô tuyến thứ 100?

Cho \(y = f\left( x \right)\) có đạo hàm tại \({x_0}\) là \(f'\left( {{x_0}} \right)\). Phát biểu nào sau đây là đúng?

A. \(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) + f\left( {{x_0}} \right)}}{{x + {x_0}}}\)

B. \(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\)

C. \(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x + {x_0}}}\)

D. \(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) + f\left( {{x_0}} \right)}}{{x - {x_0}}}\)

Điện lượng \(Q\) truyền trong dây dẫn là một hàm số của thời gian \(t,{\rm{ }}Q = Q\left( t \right).\) Cường độ trung bình trong khoảng \(\left| {t - {t_0}} \right|\) được xác định bởi công thức \(\frac{{Q\left( t \right) - Q\left( {{t_0}} \right)}}{{t - {t_0}}}.\) Cường độ tức thời tại thời điểm \({t_0}\) là:

A. \(\frac{{Q\left( t \right) - Q\left( {{t_0}} \right)}}{{t - {t_0}}}.\)

B. \(\mathop {\lim }\limits_{t \to 0} \frac{{Q\left( t \right) - Q\left( {{t_0}} \right)}}{{t - {t_0}}}.\)

C. \(\mathop {\lim }\limits_{t \to {t_0}} \frac{{Q'\left( t \right) - Q'\left( {{t_0}} \right)}}{{t - {t_0}}}.\)

D. \(\mathop {\lim }\limits_{t \to {t_0}} \frac{{Q\left( t \right) - Q\left( {{t_0}} \right)}}{{t - {t_0}}}.\)

Hệ số góc của tiếp tuyến của đồ thị hàm số \(y = f\left( x \right)\) tại điểm \({M_0}\left( {{x_0};f\left( {{x_0}} \right)} \right)\) là:

A. \(f\left( {{x_0}} \right).\)

B. \(f'\left( {{x_0}} \right).\)

C. \({x_0}.\)

D. \( - f'\left( {{x_0}} \right).\)

Phương trình tiếp tuyến của đồ thị hàm số \(y = f\left( x \right)\) tại điểm \({M_0}\left( {{x_0};f\left( {{x_0}} \right)} \right)\) là:

A. \(y = f\left( {{x_0}} \right)\left( {x - {x_0}} \right) + f\left( {{x_0}} \right).\)

B. \(y = f'\left( {{x_0}} \right)\left( {x + {x_0}} \right) + f\left( {{x_0}} \right).\)

C. \(y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + f\left( {{x_0}} \right).\)

D. \(y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) - f\left( {{x_0}} \right).\)

Vận tốc tức thời của chuyển động \(s = f\left( t \right)\) tại thời điểm \({t_0}\) là:

A. \(f'\left( {{t_0}} \right).\)

B. \(f\left( {{t_0}} \right) - f'\left( {{t_0}} \right).\)

C. \(f\left( {{t_0}} \right).\)

D. \( - f'\left( {{t_0}} \right).\)

Tính đạo hàm của mỗi hàm số sau bằng định nghĩa:

a) \(f\left( x \right) = x + 2;\)

b) \(g\left( x \right) = 4{x^2} - 1;\)

c) \(h\left( x \right) = \frac{1}{{x - 1}}.\)

Chứng minh rằng hàm số \(f\left( x \right) = \left| {x - 2} \right|\) không có đạo hàm tại điểm \({x_0} = 2,\) nhưng có đạo hàm tại mọi điểm \(x \ne 2\)?

Cho hàm số \(f\left( x \right) = {x^3}\) có đồ thị \(\left( C \right)\).

a) Viết phương trình tiếp tuyến của \(\left( C \right)\) tại điểm có hoành độ bằng \( - 1.\)

b) Viết phương trình tiếp tuyến của \(\left( C \right)\) tại điểm có tung độ bằng \(8.\)

Một vật rơi tự do có phương trình chuyển động là \(s\left( t \right) = \frac{1}{2}g{t^2}\), trong đó \(g = 9,8m/{s^2}.\)

a) Tìm vận tốc tức thời của vật tại thời điểm \(t = 3\) (s).

b) Tìm thời điểm mà vận tốc tức thời của vật tại thời điểm đó bằng \(39,2\left( {m/s} \right).\)