Bài tập 13 trang 18 SGK Hình học 11 NC
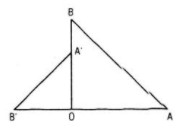
Cho hai tam giác vuông cân OAB và OA'B' có chung đỉnh O sao cho O nằm trên đoạn thẳng A'B' và nằm ngoài đoạn thẳng A'B (h.16). Gọi G và G' lần lượt là trọng tâm các tam giác OAA' và OBB'.Chứng minh GOG' là tam giác vuông cân.
Hướng dẫn giải chi tiết
Gọi Q là phép quay tâm O, góc quay π/2 (bằng góc lượng giác (OA ; OB)). Khi đó Q biến A thành B và biến A’ thành B’, tức là biến tam giác OAA’ và OBB’
Bởi vậy Q biến G (trọng tâm tam giác OAA’) thành G’ (trọng tâm tam giác OBB’).
Suy ra \(OG = OG';\widehat {GOG\prime } = \frac{\pi }{2}\)
Vậy GOG’ là tam giác vuông cân tại đỉnh O
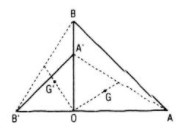
Chú ý: Phép quay Q biến trọng tâm G tam giác ABC thành trọng tâm G’ của tam giác A’B’C’ ảnh của △ABC qua Q được suy ra từ phép quay Q biến trung điểm I của đoạn thẳng
-- Mod Toán 11 HỌC247
-


trong mặt phẳng Oxy , cho đường tròn (C):x2+(y-1)2=4 . tìm phương trình ảnh của (C) qua phép quay tâm O , góc quay (90o) .
Theo dõi (0) 1 Trả lời -


Bài 1.37 trang 39 sách bài tập Hình học 11
bởi Nguyễn Quang Thanh Tú
 29/10/2018
Bài 1.37 (Sách bài tập - trang 39)
29/10/2018
Bài 1.37 (Sách bài tập - trang 39)Trong mặt phẳng Oxy cho đường thẳng d có phương trình \(x+y-2=0\). Hãy viết phương trình của đường thẳng d' là ảnh của d qua phép quay tâm O góc \(45^0\) ?
Theo dõi (0) 1 Trả lời -


Trong mặt phẳng Oxy cho điểm A(1;0). Xác định tọa độ ảnh của điểm A qua phép quay tâm O góc quay bằng \(\frac{\pi }{2}\).
Theo dõi (0) 2 Trả lời






