Bài tập 1 trang 73 SBT Toán 11 Tập 2 Chân trời sáng tạo
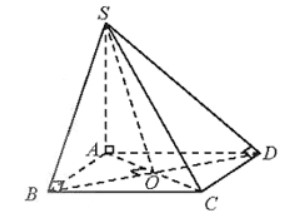
Cho hình chóp S.ABC có đáy là hình vuông tâm O cạnh a, SA = a√3a√3 và vuông góc với đáy. Xác định và tính góc giữa:
a) SB và (ABCD);
b) SC và (ABCD);
c) SD và (ABCD);
d) SB và (SAC).
Hướng dẫn giải chi tiết Bài tập 1
a) Ta có: {SA⊥(ABCD)SB∩(ABCD)=B
Suy ra AB là hình chiếu của SB trên (ABCD).
Do đó (SB, (ABCD)) = (SB, AB).
Trong tam giác SAB vuông tại A, ta có:
tan^SBA=SAAB=√3⇒^SBA=60°.
Vậy (SB,(ABCD))=^SBA=60°.
b) Tương tự câu a) ta xác định được (SC, (ABCD)) = (SC, AC).
Trong tam giác SAC vuông tại A, ta có:
tan^SCA=SAAC=√3√2⇒^SCA≈50,8°.
Vậy (SC,(ABCD))=^SCA≈50,8°.
c) Tương tự câu a) ta xác định được (SD, (ABCD)) = (SD,AD).
Trong tam giác SAD vuông tại A, ta có:
tan^SDA=SAAD=√3⇒^SDA=60°.
Vậy (SD,(ABCD))=^SDA=60°.
d) Ta có: {BD⊥ACBD⊥SA
⇒ BD ⊥ (SAC) hay BO ⊥ (SAC). (1)
Mà SB ∩ (SAC) = S. (2)
Từ (1) và (2) suy ra SO là hình chiếu của SB trên (SAC).
Do đó: (SB, (SAC)) = (SB, SO).
Trong tam giác SBO vuông tại O, ta có:
BO=12BD=a√22,SB=2a.
⇒sin^BSO=BOSB=√24⇒^BSO≈20,7°.
Vậy (SB,(SAC))=^BSO≈20,7°.
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Giải Bài 4 trang 85 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 5 trang 85 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Bài tập 2 trang 73 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 3 trang 73 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 4 trang 73 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST





