Giải Bài 4 trang 85 SGK Toán 11 Chân trời sáng tạo tập 2
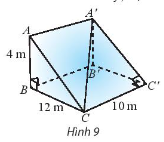
Một con dốc có dạng hình lăng trụ đứng tam giác với kích thước như trong Hình 9.
a) Tính số đo góc giữa đường thẳng \(CA'\) và .
b) Tính số đo góc nhị diện cạnh \(CC'\).
Hướng dẫn giải chi tiết Bài 4
Phương pháp giải
‒ Cách tính góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng.
‒ Cách xác định góc nhị diện \(\left[ {{P_1},d,{Q_1}} \right]\)
Bước 1: Xác định \(c = \left( {{P_1}} \right) \cap \left( {{Q_1}} \right)\).
Bước 2: Tìm mặt phẳng \(\left( R \right) \supset c\).
Bước 3: Tìm \(p = \left( R \right) \cap \left( {{P_1}} \right),q = \left( R \right) \cap \left( {{Q_1}} \right),O = p \cap q,M \in p,N \in q\).
Khi đó \(\left[ {{P_1},d,{Q_1}} \right] = \widehat {MON}\).
Lời giải chi tiết
a) Ta có:
\(\left. \begin{array}{l}BB' \bot \left( {A'B'C'} \right) \Rightarrow BB' \bot A'B'\\A'B' \bot B'C'\end{array} \right\} \Rightarrow A'B' \bot \left( {CC'B'B} \right)\\ \Rightarrow \left( {CA',\left( {CC'B'B} \right)} \right) = \left( {CA',CB'} \right) = \widehat {A'CB'}\\B'C = \sqrt {BB{^2} + B{C^2}} = 2\sqrt {61} ,A'B' = AB = 4\\\tan \widehat {A'CB'} = \frac{{A'B'}}{{B'C}} = \frac{2}{{\sqrt {61} }} \Rightarrow \widehat {A'CB'} \approx 14,{4^ \circ }\)
Vậy \(\left( {CA',\left( {CC'B'B} \right)} \right) \approx 14,{4^ \circ }\)
b) \(CC' \bot \left( {ABC} \right) \Rightarrow CC' \bot AC,CC' \bot BC\)
Vậy \(\widehat {ACB}\) là góc nhị diện cạnh \(CC'\).
\(\tan \widehat {ACB} = \frac{{AB}}{{AC}} = \frac{1}{3} \Rightarrow \widehat {ACB} \approx 18,{4^ \circ }\)
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Giải Bài 2 trang 85 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 3 trang 85 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 5 trang 85 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Bài tập 1 trang 73 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 2 trang 73 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 3 trang 73 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 4 trang 73 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST





