Bài 3 trang 115 SGK Toán 11 Tập 2 Cánh diều
Cho hình lăng trụ đứng \(ABCD.A'B'C'D'\) có đáy \(ABCD\) là hình vuông cạnh \(a\). Góc giữa đường thẳng \(AC\) và mặt phẳng \(\left( {ABCD} \right)\) bằng \({60^ \circ }\).
a) Chứng minh rằng hai mặt phẳng \(\left( {ACC'A'} \right)\) và \(\left( {BDD'B'} \right)\) vuông góc với nhau.
b) Tính khoảng cách giữa hai đường thẳng \(AB\) và \(CD'\).
Hướng dẫn giải chi tiết Bài 3
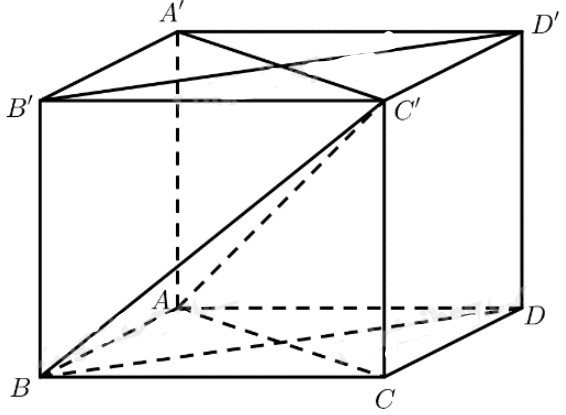
a) \(ABCD\) là hình vuông \( \Rightarrow AC \bot B{\rm{D}}\)
\(BB' \bot \left( {ABCD} \right) \Rightarrow BB' \bot AC\)
\(\left. \begin{array}{l} \Rightarrow AC \bot \left( {B{\rm{DD'B'}}} \right)\\AC \subset \left( {ACC'A'} \right)\end{array} \right\} \Rightarrow \left( {ACC'A'} \right) \bot \left( {B{\rm{DD}}'B'} \right)\)
b) \(ABCD\) là hình vuông \( \Rightarrow AB\parallel C{\rm{D}}\)
\(CDD'C'\) là hình chữ nhật \( \Rightarrow C{\rm{D}}\parallel C'{\rm{D}}'\)
\( \Rightarrow AB\parallel C'{\rm{D}}' \Rightarrow d\left( {AB,C'{\rm{D}}'} \right) = d\left( {B,C'{\rm{D}}'} \right)\)
\(A'B'C'D'\) là hình vuông \( \Rightarrow C'D' \bot B'C'\)
\(CDD'C'\) là hình chữ nhật \( \Rightarrow C'D' \bot CC'\)
\( \Rightarrow C'D' \bot \left( {BCC'B'} \right) \Rightarrow C'D' \bot BC' \Rightarrow d\left( {B,C'{\rm{D}}'} \right) = BC'\)
\(ABCD\) là hình vuông \( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \)
\(\begin{array}{l}CC' \bot \left( {ABCD} \right) \Rightarrow \left( {AC',\left( {ABCD} \right)} \right) = \left( {AC',AC} \right) = \widehat {CAC'} = {60^ \circ }\\ \Rightarrow CC' = AC.\tan \widehat {CAC'} = a\sqrt 6 \end{array}\)
\(\Delta BCC'\) vuông tại \(C \Rightarrow BC{'^2} = \sqrt {B{C^2} + CC{'^2}} = a\sqrt 7 \)
Vậy \(d\left( {AB,C'{\rm{D}}'} \right) = a\sqrt 7 \).
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Bài 1 trang 115 SGK Toán 11 Tập 2 Cánh diều - CD
Bài 2 trang 115 SGK Toán 11 Tập 2 Cánh diều - CD
Bài 4 trang 115 SGK Toán 11 Tập 2 Cánh diều - CD
Bài 5 trang 115 SGK Toán 11 Tập 2 Cánh diều - CD
Bài 6 trang 115 SGK Toán 11 Tập 2 Cánh diều - CD
Bài 7 trang 115 SGK Toán 11 Tập 2 Cánh diều - CD
Bài tập 51 trang 117 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 52 trang 117 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 53 trang 117 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 54 trang 117 SBT Toán 11 Tập 2 Cánh diều - CD





