Giải bài 48 trang 62 SBT Toán 10 Cánh diều tập 1
Cho hàm số \(y = f\left( x \right)\) có đồ thị ở Hình 24
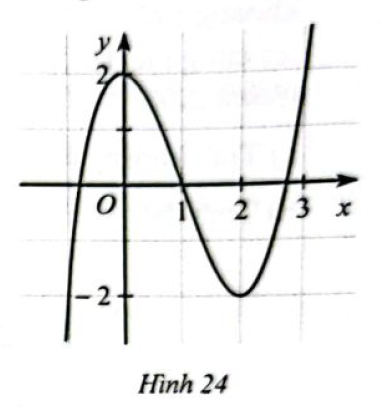
a) Chỉ ra khoảng đồng biến và khoảng nghịch biến của hàm số \(y = f\left( x \right)\)
b) Nêu tung độ giao điểm của đồ thị hàm số \(y = f\left( x \right)\) với trục \(Oy\)
Hướng dẫn giải chi tiết Bài 48
Phương pháp giải
Quan sát đồ thị hàm số, trên \((a;b)\)
+ Đồ thị hàm số đi lên (từ trái qua phải) thì hàm số đồng biến trên \((a;b)\)
+ Đồ thị hàm số đi xuống (từ trái qua phải) thì hàm số nghịch biến trên \((a;b)\)
Lời giải chi tiết
a) Quan sát đồ thị hàm số, ta thấy:
+ Đồ thị hàm số đi lên (từ trái qua phải) ứng với \(x \in \left( { - \infty ;0} \right) \cup (2; + \infty )\)
+ Đồ thị hàm số đi xuống (từ trái qua phải) ứng với \(x \in (0;2)\)
Do đó hàm số đồng biến trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\)và nghịch biến trên khoảng \(\left( {0;2} \right)\).
b) Giao điểm của hàm số với trục Oy có hoành độ là \(x = 0\)
Do đó tung độ của điểm đó là: \(y = f(0) = 2\)
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Giải bài 46 trang 61 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 47 trang 62 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 49 trang 62 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 50 trang 62 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 51 trang 62 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 52 trang 62 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 53 trang 62 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 54 trang 63 SBT Toán 10 Cánh diều tập 1 - CD





