Giải bài 43 trang 61 SBT Toán 10 Cánh diều tập 1
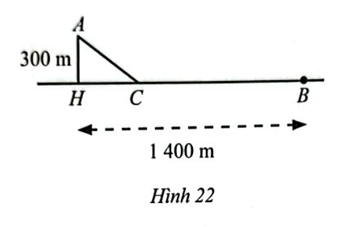
Một người đi bộ xuất phát từ B trên một bờ sông (coi là đường thẳng) với vận tốc 6 km/h để gặp một người chèo thuyền xuất phát cùng lúc từ vị trí A với vận tốc 3 km/h. Nếu người chèo thuyền di chuyển theo đường vuông góc với bờ thì phải đi một khoảng cách AH = 300 m và người đi bộ tại địa điểm cách B một khoảng BH = 1 400 m. Tuy nhiên, nếu di chuyển theo cách đó thì hai người không tới cùng lúc. Để hai người đến cùng lúc thì mỗi người cùng di chuyển về vị trí C (Hình 22).
a) Tính khoảng các CB
b) Tính thời gian từ khi hai người xuất phát cho đến khi gặp nhau cùng lúc
Hướng dẫn giải chi tiết Bài 43
Phương pháp giải
Gọi \(CH = x\) (m). Biểu diễn AC và BC qua x. Giải phương trình \(\frac{{AC}}{{3.000}} = \frac{{BC}}{{6.000}}\) tìm ra CH
Lời giải chi tiết
a) Đặt \(CH = x\) (m) (\(x > 0\)). Ta có: \(AC = \sqrt {A{H^2} + C{H^2}} = \sqrt {{{300}^2} + {x^2}} ,BC = 1\;400 - CH = 1\;400 - x\)
Đổi 6 km/h = 6000 m/h; 3 km/h = 3000 m/h;
Thời gian đi đến lúc gặp nhau của người đi bộ là: \(\frac{{BC}}{{6000}} = \frac{{1400 - x}}{{6000}}\)
Thời gian đi đến lúc gặp nhau của người chèo thuyền là: \(\frac{{AC}}{{3000}} = \frac{{\sqrt {{{300}^2} + {x^2}} }}{{3000}}\)
Vì hai người gặp nhau cùng lúc tại C nên ta có: \(\frac{{\sqrt {{{300}^2} + {x^2}} }}{{3000}} = \frac{{1400 - x}}{{6000}} \Leftrightarrow 2\sqrt {{{300}^2} + {x^2}} = 1400 - x\) (với \(x > 0\))
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}x > 0\\1400 - x \ge 0\\4\left( {{{300}^2} + {x^2}} \right) = {\left( {1400 - x} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0 < x \le 1400\\4{x^2} + 360000 = {x^2} - 2800x + {1400^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}0 < x \le 1400\\3{x^2} + 2800x - 1600000 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0 < x \le 1400\\\left[ \begin{array}{l}x = - \frac{{4000}}{3}\;(L)\\x = 400\;\end{array} \right.\quad \end{array} \right. \Leftrightarrow x = 400\;\end{array}\)
Vậy khoảng cách \(BC = 1400 - 400 = 1000\) (m)
b) Thời gian từ khi hai người xuất phát cho đến khi gặp nhau là thời gian người đi bộ bắt đầu di chuyển cho đến khi gặp người chèo thuyền tại C là:
\(\frac{{BC}}{{6000}} = \frac{{1000}}{{6000}} = \frac{1}{6}\) (giờ) = 10 phút.
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





