Giải bài 4 trang 101 SGK Toán 10 Chân trời sáng tạo tập 1
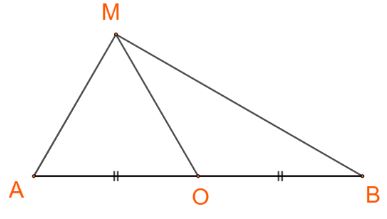
Cho đoạn thẳng AB có O là trung điểm và cho điểm M tùy ý. Chứng minh rằng:
\(\overrightarrow {MA} .\overrightarrow {MB} = {\overrightarrow {MO} ^2} - {\overrightarrow {OA} ^2}\)
Hướng dẫn giải chi tiết Bài 4
Phương pháp giải
Sử dụng hằng đẳng thức \({a^2} - {b^2} = \left( {a - b} \right)\left( {a + b} \right)\) phân tích \({\overrightarrow {MO} ^2} - {\overrightarrow {OA} ^2}\)
Lời giải chi tiết
Ta có: \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow 0 \Leftrightarrow - \overrightarrow {OA} = \overrightarrow {OB} \)
\(\Rightarrow {\overrightarrow {MO} ^2} - {\overrightarrow {OA} ^2} = \left( {\overrightarrow {MO} - \overrightarrow {OA} } \right)\left( {\overrightarrow {MO} + \overrightarrow {OA} } \right) \\= \left( {\overrightarrow {MO} + \overrightarrow {OB} } \right)\left( {\overrightarrow {MO} + \overrightarrow {OA} } \right) = \overrightarrow {MB} .\overrightarrow {MA} \) (đpcm)
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Giải bài 2 trang 101 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 101 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 101 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 101 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 100 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 100 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 101 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 101 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 101 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST