Giải bài 4.1 trang 47 SBT Toán 10 Kết nối tri thức tập 1
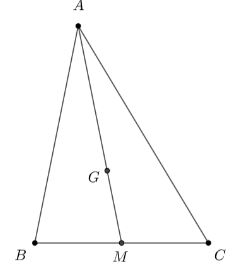
Cho tam giác \(ABC\). Gọi \(M\) là trung điểm của cạnh \(BC\) và \(G\) là trọng tâm của tam giác. Trong các khẳng định sau, khẳng định nào là một khẳng định đúng?
a) Hai vectơ \(\overrightarrow {GA} \) và \(\overrightarrow {GM} \) cùng phương.
b) Hai vectơ \(\overrightarrow {GA} \) và \(\overrightarrow {GM} \) cùng hướng.
c) Hai vectơ \(\overrightarrow {GA} \) và \(\overrightarrow {GM} \) ngược hướng.
d) Độ dài của vectơ \(\overrightarrow {AM} \) bằng ba lần độ dài của vectơ \(\overrightarrow {MG} \).
Hướng dẫn giải chi tiết Bài 4.1
Phương pháp giải
- Sử dụng tính chất của trọng tâm tam giác
- Các định các vectơ cùng phương, cùng hướng hay ngược hướng.
Lời giải chi tiết
Xét \(\Delta ABC\) có: \(M\) là trung điểm của \(BC\)
\(G\) là trọng tâm của \(\Delta ABC\)
\( \Rightarrow \,\,AG = \frac{2}{3}GM.\)
mặt khác \(\overrightarrow {GA} \) và \(\overrightarrow {GM} \) ngược hướng
nên \(\left| {\overrightarrow {AM} } \right| = 3\left| {\overrightarrow {MG} } \right|\)
Vậy khẳng định a,c,d là khẳng định đúng còn khẳng định b là khẳng định sai.
-- Mod Toán 10 HỌC247
-


Cho ba vectơ sau \(\overrightarrow{a},\) \(\overrightarrow{b}\), \(\overrightarrow{c}\) đều khác vec tơ \(\overrightarrow{0}\). Khẳng định "Nếu hai vectơ \(\overrightarrow{a}\), \(\overrightarrow{b}\) cùng phương với \(\overrightarrow{c}\) thì \(\overrightarrow{a}\), \(\overrightarrow{b}\) cùng phương" đúng hay sai
bởi An Vũ
 04/09/2022
Theo dõi (0) 1 Trả lời
04/09/2022
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Giải bài 4.4 trang 50 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.5 trang 50 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.2 trang 47 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.3 trang 47 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.4 trang 47 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.5 trang 47 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.6 trang 48 SBT Toán 10 Kết nối tri thức tập 1 - KNTT