Giải bài 3 trang 79 SBT Toán 10 Chân trời sáng tạo tập 1
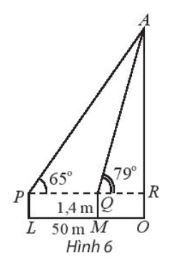
Để xác định chiều cao của một tòa nhà cao tầng, một người đứng tại điểm M, sử dụng giác kế nhìn thấy đỉnh tòa nhà với góc nâng \(\widehat {RQA} = 79^\circ \), người đó lùi ra xa một khoảng cách \(LM = 50\) m thì nhìn thấy đỉnh tòa nhà với góc nâng \(\widehat {RPA} = 65^\circ \). Hãy tính chiều cao của tòa nhà, biết rằng khoảng cách từ mặt đất đến ống ngắm của giác kế đó là \(PL = QM = 1,4\) m (hình 6)
Hướng dẫn giải chi tiết Bài 3
Phương pháp giải
+ Xác định chiều cao của nhà cao tầng
+ Xác định gGóc \(\widehat {AQR}\)
+ Áp dụng định lí sin vào tam giác APQ
+ Xét tam giác AQR => AO
Lời giải chi tiết
Ta có chiều cao của nhà cao tầng là \(AO = AR + RO = AR + 1,4\)
Góc \(\widehat {AQR}\) là góc ngoài của tam giác APQ tại đỉnh Q suy ra \(\widehat {AQR} = \widehat {APQ} + \widehat {QAP} \Rightarrow \widehat {QAP} = \widehat {AQR} - \widehat {APQ} = 79^\circ - 65^\circ = 14^\circ \)
Áp dụng định lí sin vào tam giác APQ ta có:
\(\frac{{PQ}}{{\sin \widehat {PAQ}}} = \frac{{AQ}}{{\sin \widehat {APQ}}} = \frac{{50}}{{\sin 14^\circ }} \Rightarrow AQ = \frac{{50}}{{\sin 14^\circ }}.\sin 65^\circ \)
Xét tam giác AQR ta có:
\(\frac{{AR}}{{\sin \widehat {AQR}}} = \frac{{AQ}}{{\sin \widehat {ARQ}}} = \frac{{\frac{{50}}{{\sin 14^\circ }}.\sin 65^\circ }}{{\sin 90^\circ }} \Rightarrow AR = \frac{{\frac{{50}}{{\sin 14^\circ }}.\sin 65^\circ }}{{\sin 90^\circ }}.\sin 79^\circ \simeq 183,87\)
\( \Rightarrow AO \simeq 183,87 + 1,4 = 185,27\)
Vậy tòa nhà cao xấp xỉ 185,27 m
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Giải bài 1 trang 79 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 79 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 79 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 79 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 79 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST