Giải bài 5 trang 79 SBT Toán 10 Chân trời sáng tạo tập 1
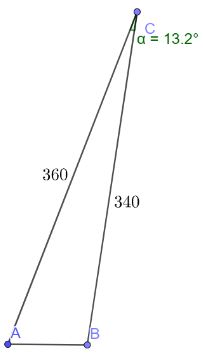
Tính khoảng cách AB giữa nóc hai tòa cao ốc. Cho biết khoảng cách từ hai điểm đó đến một vệ tinh viễn thông lần lượt là 360 km, 340 km và góc nhìn từ vệ tinh đến A và B là \(13,2^\circ \) (hình 8)
Hướng dẫn giải chi tiết Bài 5
Phương pháp giải:
Áp dụng định lí côsin
Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - 2bc\cos A\\{b^2} = {c^2} + {a^2} - 2ca\cos B\\{c^2} = {a^2} + {b^2} - 2ab\cos C\end{array}\)
Lời giải chi tiết
Áp dụng định lí côsin ta có:
\(\begin{array}{l}A{B^2} = A{C^2} + B{C^2} - 2AC.BC.\cos C\\ \Rightarrow AB = \sqrt {A{C^2} + B{C^2} - 2AC.BC.\cos C} = \sqrt {{{360}^2} + {{340}^2} - 2.360.340.\cos 13,2^\circ } \simeq 82,87\end{array}\)Vậy khoảng cách AB giữa hai nóc tòa cao ốc xấp xỉ 82,87 km
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.