Giải bài 1 trang 94 SBT Toán 10 Chân trời sáng tạo tập 1
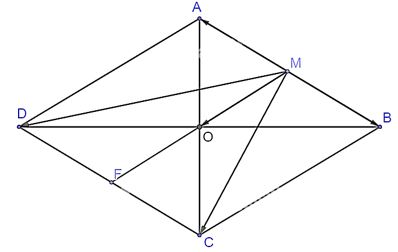
Cho hình thoi ABCD và M là trung điểm của cạnh AB, N là trung điểm cạnh CD. Chứng minh rằng:
\(\overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MB} + \overrightarrow {MD} = \overrightarrow {MN} \)
Hướng dẫn giải chi tiết Bài 1
Phương pháp giải
Sử dụng tính chất trung điểm \(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} \) (với M là trung điểm của BC)
Lời giải chi tiết
Gọi O là giao điểm của hai đường chéo, suy ra O là trung điểm của AC, BD, MN
Áp dụng tính chất trung điểm ta có:
\(\begin{array}{l}\overrightarrow {MA} + \overrightarrow {MC} = 2\overrightarrow {MO} = \overrightarrow {MN} \\\overrightarrow {MB} + \overrightarrow {MD} = 2\overrightarrow {MO} = \overrightarrow {MN} \end{array}\)
Từ đó ta có \(\overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MB} + \overrightarrow {MD} = \overrightarrow {MN} \) (đpcm)
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Giải bài 7 trang 93 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 8 trang 93 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 94 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 94 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 94 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 94 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 94 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 94 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST