Giải bài 6 trang 94 SBT Toán 10 Chân trời sáng tạo tập 1
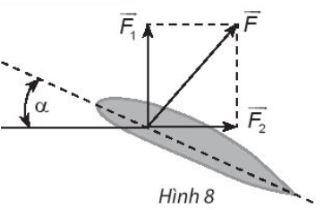
Khi máy bay nghiêng cánh một góc \(\alpha \), lực \(\overrightarrow F \) của không khí tác động vuông góc với cánh và bằng tổng của lực nâng \(\overrightarrow {{F_1}} \) và lực cản \(\overrightarrow {{F_2}} \) (hình 8). Cho biết \(\alpha = 45^\circ \) và \(\left| {\overrightarrow F } \right| = a\). Tính \(\left| {\overrightarrow {{F_1}} } \right|\) và \(\left| {\overrightarrow {{F_2}} } \right|\)
Hướng dẫn giải chi tiết Bài 6
Phương pháp giải
Từ giả thiết ta có: \(\widehat {AOB} = \widehat {AOC} + \widehat {COB}\)
Suy ra \(\widehat {AOC} = \widehat {BOQ}\)
Ta có: \(OA = OB = OC.\cos 45^\circ \), \(\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {OA} } \right| \)
Vậy \(\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| \)
Lời giải chi tiết
Ta có: \(\overrightarrow {{F_1}} = \overrightarrow {OA} ,\overrightarrow {{F_2}} = \overrightarrow {OB} ,\overrightarrow F = \overrightarrow {OC} \)
Từ giả thiết ta có: \(\widehat {AOB} = \widehat {AOC} + \widehat {COB} = 90^\circ ,\widehat {COQ} = \widehat {COB} + \widehat {BOQ} = 90^\circ \)
Suy ra \(\widehat {AOC} = \widehat {BOQ} = \alpha = 45^\circ \) (\(\widehat {BOQ}\) đối đỉnh với \(\alpha \))
Suy ra \(\widehat {COB} = 90^\circ - \widehat {BOQ} = 45^\circ \)
Từ đó ta có: \(OA = OB = OC.\cos 45^\circ = a.\frac{{\sqrt 2 }}{2} = \frac{{a\sqrt 2 }}{2}\)
\(\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {OA} } \right| = OA = \frac{{a\sqrt 2 }}{2};\left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {OB} } \right| = OB = \frac{{a\sqrt 2 }}{2}\)
Vậy ta có \(\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = \frac{{a\sqrt 2 }}{2}\)
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.