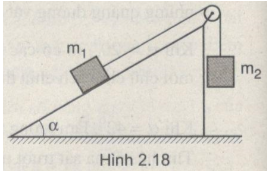
Trong hệ ở Hình 2.18,ta có : \({m_1} = 500g;\alpha = {30^0};\) các hệ số ma sát trượt và ma sát nghỉ giữa vật 1 và mặt phẳng nghiêng là \({\mu _t} = {\mu _n} = 0,2.\) Mặt phẳng nghiêng được giữ cố định. Hãy tính gia tốc của mỗi vật m1, m2 và lực ma sát giữa vật 1 với mặt phẳng nghiêng trong các trường hợp :
a) m1=500g;
b) m2=200g.
Trả lời (1)
-
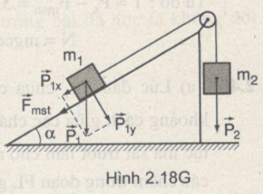
a)Nhận xét : \({P_2} > {P_{1x}} + {F_{msn\max }}\) nên vật m1 chuyển động lên trên, vật m2 chuyểnđộng xuống dưới (Hình 2.18G). Gia tốc của hệ bằng :
\(\eqalign{ & a = {{{P_2} - {P_{1x}} - {F_{mst}}} \over {{m_1} + {m_2}}} \cr & = {{{m_2}g - {m_1}g\sin \alpha - {m_1}{\mu _t}g\cos \alpha } \over {{m_1} + {m_2}}} \cr & = 1,6m/{s^2} \cr} \)
Trong đó ta đã thay \({F_{msn\max }} = {F_{mst}},\) bằng :
\({F_{mst}} = {\mu _t}{m_1}g\cos \alpha \approx 0,85N\)
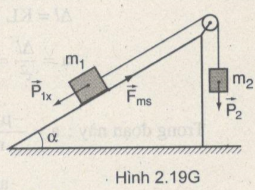
b)Trong trường hợp này ta nhận thấy :
\({P_{1x}} < {P_2} + {F_{msn\max }}(1)\)
Nên hệ không chuyển động (Hình 2.19G)
Ta có a =0.
Lúc này lực ma sát nghỉ chưa đạt tới giá trị cực đại :
\({F_{msn}} = {P_{1x}} - {P_2} = g({m_1}\sin \alpha - {m_2}) = 0,49N\)
 bởi Vũ Hải Yến
bởi Vũ Hải Yến 04/01/2022
Like (0) Báo cáo sai phạm
04/01/2022
Like (0) Báo cáo sai phạm
Nếu bạn hỏi, bạn chỉ thu về một câu trả lời.
Nhưng khi bạn suy nghĩ trả lời, bạn sẽ thu về gấp bội!

Lưu ý: Các trường hợp cố tình spam câu trả lời hoặc bị báo xấu trên 5 lần sẽ bị khóa tài khoản
Các câu hỏi mới
-
Hai xe ô tô khởi hành từ hai điểm A và B cách nhau 100km nếu 2 ô tô đi ngược chiều nhau sẽ cách nhau 1h nếu đi cùng chiều thì sẽ cách nhau 12h. Tinh vận tốc mỗi xe
25/11/2022 | 0 Trả lời
-
Hằng ngày, Hùng được bố đèo đi học bằng xe máy với tốc độ 40km/h về phía Bắc. Sau khi đi được 5km thì tới ngã tư. Tại đây, Hùng xuống xe và tiếp tục đi bộ tới trường theo hướng Đông trong 10 phút với tốc độ 3km/h. Tìm:
a. Quãng đường từ nhà Hùng tới trường?
b. Tính tốc độ trung bình của Hùng?
29/11/2022 | 0 Trả lời
-
Giữ nguyên độ lớn các điện tích và đem chúng đặt trong môi trường có hằng số điện môi là 4 thì lực tương tác giữa chúng là bao nhiêu khi 2 điện tích cách nhau một khoảng 10cm?
07/12/2022 | 0 Trả lời
-
Một vật khối lượng 800g được móc vào 1 lực kế .Lấy g=10m/s2 a)Tính số chỉ của lực kế b)Khi nhúng chìm hoàn toàn vật trong nước thì thấy lk chỉ 6.2N. Tính Thể tích vật. Biết KL riêng của nước là 1000kg/m3
08/12/2022 | 0 Trả lời
-
đây là bài thầy cho mình cần gấp
19/12/2022 | 0 Trả lời
-
Một vật có khối lượng 1 kg đang đứng yên thì được kéo theo phương ngang trên mặt phẳng ngang với 1 lực Fk=8 N độ lớn không đổi. Hệ số ma sát 0,1 lấy g=10m/s2 .
a. Tính a?
b. Tìm s khi vật đi được 10s
c. Để làm cho vật chuyển động thì cần lực Fk là bao nhiêu khi Fk hợp với phương ngang trên mặt phẳng và hướng lên một góc 30o ?
20/12/2022 | 1 Trả lời
-
Kéo một vật có khối lượng 4kg theo phương thẳng đứng từ mặt đất. Vật chuyển động thẳng đều với vận tốc 18km/h và đi được độ cao 10m. Tính công và công suất của lực kéo. Lấy g = 10m/s^2
25/02/2023 | 1 Trả lời
-
08/03/2023 | 0 Trả lời
-
a) Công của từng lực tác dụng lên vật (ma sát, lực kéo, trọng lực, phản lực cùa bề mặt)
b) Công suất trung bình của lực kéo.
10/03/2023 | 0 Trả lời
-
(1) Điều chỉnh con trượt để thước trung với vị trí đánh dấu ban đầu và ghi F, d1, d2
(2) Treo các quá nặng vào 2 con trượt
(3) Tháo các quá nặng treo vào một con trượt
(4) Đánh dấu vị trí AB của thước và ghi giá trị F1, F2
A. 2,4,3,1 B. 1,2,3,4 C. 3,2,1,4 D. 2,4,1,3
03/05/2023 | 0 Trả lời
-
Một viên đạn có khối lượng 200 g đang bay thì nổ thành hai mảnh: Mảnh thứ nhất có khối lượng là 100 g bay với vận tốc 150 m/s, mảnh thứ hai bay với vận tốc 200 m/s và có phương vuông góc với phương vận tốc mảnh thứ nhất. Tính vận tốc của viên đạn trước khi nổ?
12/05/2023 | 0 Trả lời
-
Giúp mình nhé
15/08/2023 | 1 Trả lời
-
A. Không thay đổi dù độ lớn của lực thay đổi.
B. Tỉ lệ nghịch với độ lớn của lực gây ra gia tốc cho vật.
C. Tỉ lệ thuận với độ lớn của lực gây ra gia tốc cho vật.
D. Không xác định được.
16/08/2023 | 1 Trả lời
-
A. 32 m/s2.
B. 0,005 m/s2.
C. 3,2 m/s2.
D. 5 m/s2.
16/08/2023 | 1 Trả lời
-
Vật này rơi chạm đất sau 3s sau khi ném. Cho biết lực cản không khí tác dụng vào vật không đổi trong quá trình chuyển động. Lấy g = 10 m/s2. Lực cản của không khí tác dụng vào vật có độ lớn bằng
15/08/2023 | 1 Trả lời
-
Cho 1 cano chạy trên 1 dòng sông biết vận tốc của Cano so với bờ là 15km/h biết nước chảy có vẫn tốc 5km/h so với bờ
a) tính vận tốc của Cano khi đi cùng chiều , và khi ngược chiều
b) tính vận tốc của Cano đi vuông góc từ bờ bên này sang bờ bên kia
c) tính vận tốc của Cano khi nó đi hợp với dòng sông 1 góc 30 độ 45 độ 60 độ với dòng sông
06/10/2023 | 0 Trả lời
-
Một ô tô chuyển động đều với quãng đường S=(13,8+-0,2)m trong khoảng thời gian t=(4,0+-0,3)s. Tính tốc độ trung bình chuyển động của ô tô
15/10/2023 | 0 Trả lời
-
Giải giúp mình bài này nhé! Một thuyền chuyển động xuôi dòng từ A đến B rồi chuyển động ngược dòng từ B đến A với tổng thời gian là 5 giờ. Biết dòng nước chạy với vận tốc 1,4m/s so với bờ , vận tốc thuyền so với dòng nước là 24km/h. Tính quảng đường AB
31/10/2023 | 0 Trả lời
-
Ô tô chạy đoạn AB mất 7h. Ở 1/3 đoạn đường đầu chạy tốc độ 40km/h, Ở 2/3 đoạn đường sau chạy tốc độ 60km/h. Tính quãng đường AB (ra km)
01/11/2023 | 0 Trả lời
-
Bài 4. Một chiếc xe đang chuyển động với vận tốc v = 1 m/s thì tăng tốc, sau 2 s, xe có vận tốc v = 3 m/s. Sau đó xe tiếp tục chuyển động đều trong thời gian 1 s rồi tắt máy chuyển động chậm dần đều và đi thêm 2 s nữa rồi dừng lại. Biết khối lượng của xe là 100 kg.
a. Tính gia tốc của xe trong từng giai đoạn.
b. Lực cản tác dụng vào xe là bao nhiêu? Biết lực cản có giá trị không đổi trong cả ba giai đoạn.
c. Tính lực kéo của động cơ xe trong từng giai đoạn.19/11/2023 | 0 Trả lời
-
1 vật có khối lượng 8kg được rơi từ độ cao 180m. Cho R 10m trên dây bình phương.
a)Tính thời gian từ lúc thả vật cho tới khi chạm đất
b)Tíng quãng quãng đường vật rơi trong 2 giây cuối
c) tính công của trọng lực trong hai giây cuối
04/01/2024 | 0 Trả lời
-
Một ô tô khối lượng 2 tấn chạy trên đoạn đường phẳng có hệ số ma sát là 0,1. Lấy g = 9,8m/s2. Tính lực kéo của động cơ ôtô khi:
a. Ôtô chạy nhanh dần đều với gia tốc 2 m/s2 trên đường nằm ngang.
b. Ôtô chạy lên dốc với vận tốc không đổi. Mặt đường có độ dốc 4% (góc nghiêng α của mặt đường có sinα = 0,04).
c. Vận tốc của vật sau khi trượt được một đoạn đường dài s = 0,9m.
07/01/2024 | 0 Trả lời
-
a, sau khi ném được 0,5s thì quả bóng ở độ cao 4,5m
b, sau khoảng 2s thì quả bóng chạm đất
c,quả bóng ở độ cao trên 5m thì trong khoảng tg từ 0,55s-1,5s
d, độ cao lớn nhất của quả bóng so với mặt đất xấp xỉ 6,1m
10/03/2024 | 0 Trả lời
-
Người ấy tác dụng một lực F theo phương vuông góc với tấm gỗ vào đầu trên của tấm gỗ để giữ cho nó hợp với mặt đất một góc am pha =30 độ. Tính độ lớn lực người tác dụng vào tấm gỗ ?
23/03/2024 | 0 Trả lời
-
Cho thời gian va chạm giữa vật và bóng là 0,04s.a,hãy xác định độ biến thiên động lượng của trái bóng trước và sau va chạm . b, tính lực của tường tác dụng vào trái bóng
16/04/2024 | 0 Trả lời






