-
Câu hỏi:
Tìm tất cả các giá trị của m để tam thức f(x)=mx2–x+mf(x)=mx2–x+m luôn dương với ∀x∈R.
- A. m > 0.
- B. m < 0.
- C. m > 1212.
- D. m < 1212.
Lời giải tham khảo:
Đáp án đúng: C
Đáp án đúng là: C
+) Với m = 0 thì f(x) = – x, f(x) > 0 ⇔ – x > 0 ⇔ x < 0. Do đó m = 0 không thỏa mãn.
Ta có để f(x) = mx2 – x + m > 0, ∈ R ⇔{m>0Δ=(−1)2−4.m.m<0⇔{m>01−4m2<0
Xét biểu thức g(m) = 1 – 4m2 có ∆ = 16 > 0, hai nghiệm phân biệt là m = 12, m = −12 và a = – 4 < 0
Ta có bảng xét dấu
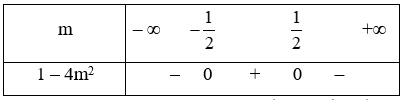
Dựa vào bảng xét dấu ta có 1 – 4m2 < 0
∈ ( − ∞ ; − ) ∪ ( ; + ∞ ) Vậy để f(x) = mx2 – x + m nhận giá trị dương , ∈ R
⇔ m > 12.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Bảng xét dấu nào sau đây là bảng xét dấu của tam thức f(x)=x2+2x+1 là:
- Biểu thức nào sau đây là tam thức bậc hai
- Với x thuộc tập hợp nào dưới đây thì đa thức f(x)=x2–6x+8 không dương?
- Tam thức nào sau đây nhận giá trị âm với mọi x < 1
- Cho hàm số f(x)=mx2–2mx+m–1. Giá trị của m để f(x) < 0, ∀x∈R.
- Tìm tất cả các giá trị thực của tham số m để f(x)=(m–3)x2+(m+2)x–4 nhận giá trị không dương với mọi giá trị của x.
- Tìm tất cả các giá trị của m để tam thức f(x)=mx2–x+m luôn dương với ∀x∈R
- Tam thức y=–x2–3x–4 nhận giá trị âm khi và chỉ khi
- Cho f(x)=mx2–2x–1. Xác định m để f(x) < 0 với mọi x∈ ℝ.
- Xác định m để biểu thức f(x)=(m+2)x2–3mx+1 là tam thức bậc hai
- Bạn An muốn mua một cây bút mực và một cây bút chì. Các cây bút mực có 8 màu khác nhau,
- Một người vào cửa hàng ăn, người đó chọn thực đơn gồm 1 món ăn trong 5 món,
- Cho các số 1, 5, 6, 7 có thể lập được bao nhiêu số tự nhiên có 4 chữ số với các chữ số đôi một khác nhau từ các số trên.
- Cho các chữ số 2, 3, 4, 5, 6, 7 số các số tự nhiên chẵn có 3 chữ số lập thành từ các chữ số đã cho là:
- Giả sử ta dùng 5 màu để tô cho 3 nước khác nhau trên bản đồ và không có màu nào được dùng hai lần.
- Có bao nhiêu cách xếp 5 người thành một hàng dọc
- Tên 15 học sinh được ghi vào 15 tờ giấy để vào trong hộp. Có bao nhiêu cách chọn tên 4 học sinh để cho đi du lịch
- Một hội đồng gồm 2 giáo viên và 3 học sinh được chọn từ một nhóm 5&nbs
- Trong khai triển nhị thức (a+2)n+6 (n ∈ ℕ). Có tất cả 17 số hạng. Vậy n bằng
- Hệ số của x7 trong khai triển của (3–x)9 là
- Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng song song với trục Ox?
- Một đường thẳng có bao nhiêu vectơ chỉ phương?
- Viết phương trình tổng quát của đường thẳng d đi qua điểm M(-1; 2) và song song với trục Ox?
- Phương trình đường thẳng cắt hai trục tọa độ tại A(-2 ; 0) và B(0 ; 3) là:
- Phương trình tổng quát của đường thẳng đi qua điểm A(2 ; -1) và B(2 ; 5) là:
- Xét vị trí tương đối của hai đường thẳng: d1: x – 2y + 1 = 0 và d2: – 3x + 6y – 10 = 0
- Tính góc tạo bởi giữa hai đường thẳng: d1: 2x - y - 10 = 0 và d2: x - 3y + 9 = 0
- Tọa độ tâm I và bán kính R của đường tròn (C):(x−1)2+(y+3)2=16 là:
- Đường tròn (C):x2+y2−6x+2y+6=0 có tâm I, bán kính R lần lượt là:
- Dạng chính tắc của hypebol là?







