Giải Bài tập 26.1 trang 48 SBT Vật lý 10 Kết nối tri thức
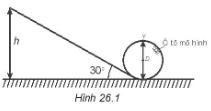
Một ô tô mô hình được thả nhẹ từ trạng thái nghỉ từ độ cao h của một cái rãnh không ma sát. Rãnh được uốn thành đường tròn có đường kính D ở phía cuối như trên Hình 26.1. Ô tô này trượt trên rãnh được cả vòng tròn mà không bị rơi. Giá trị tối thiểu của h là:
A. \(\frac{5D}{4}\).
B. \(\frac{3D}{2}\).
C. \(\frac{5D}{2}\).
D. \(\frac{5D}{3}\).
Hướng dẫn giải chi tiết Bài tập 26.1
Phương pháp giải:
Áp dụng công thức tính cơ năng \(W = \frac{1}{2}m{v^2}\)
Sử dụng công thức: Fht = P + N
Lời giải chi tiết:
Chọn mốc tính thế năng tại mặt phẳng ngang.
Cơ năng tại đỉnh dốc: \(W_{1}=W_{d1}+W_{t1}=\frac{1}{2}m.0^{2}+mgh=mgh\)
Cơ năng tại điểm cao nhất của vòng tròn: \(W_{2}=W_{d2}+W_{t2}=\frac{1}{2}mv^{2}+mgD\)
Do bỏ qua ma sát nên cơ năng coi như bảo toàn:
\(W_{1}=W_{2}\Rightarrow mgh=\frac{1}{2}mv^{2}+mgD\Rightarrow v^{2}=2g(h-D)\)
Khi ô tô lên đỉnh cao nhất của vòng tròn, hợp lực của trọng lực và phản lực tác dụng lên ô tô đóng vai trò là lực hướng tâm (trọng lực và phản lực có phương thẳng đứng, hướng xuống):
\( F_{ht}=P+N\Rightarrow N=F_{ht}-P=m\frac{v^{2}}{r}-mg=m\frac{2g(h-D)}{\frac{D}{2}}-mg\)
Để ô tô không bị rơi khi lên đỉnh vòng tròn thì:
\( N\geq 0\Rightarrow m\frac{2g(h-D)}{\frac{D}{2}}-mg\geq 0\Rightarrow h-D\geq \frac{D}{4}\)
\( \Rightarrow h\geq \frac{5D}{4}\Rightarrow h_{min}=\frac{5D}{4}\).
Đáp án A
-- Mod Vật Lý 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Giải câu hỏi 1 trang 105 SGK Vật Lý 10 Kết nối tri thức - KNTT
Giải câu hỏi 2 trang 105 SGK Vật Lý 10 Kết nối tri thức - KNTT
Giải Bài tập 26.2 trang 49 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 26.3 trang 49 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 26.4 trang 49 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 26.4 trang 49 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 26.6 trang 49 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 26.7 trang 49 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 26.8 trang 49 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 26.9 trang 50 SBT Vật lý 10 Kết nối tri thức - KNTT