Vật Lý 10 Chân trời sáng tạo Bài 17: Động năng và thế năng. Định luật bảo toàn cơ năng

a. Mối liên hệ giữa động năng và công

Động năng của một vật là năng lượng vật có được do chuyển động, có giá trị được tính theo công thức: \({{\rm{W}}_d} = \frac{1}{2}m.{v^2}\)

Với: m là khối lượng của vật

         v là tốc độ của vật tại thời điểm khảo sát

Trong hệ SI, động năng có đơn vị là joule (J)

Người, sóng biển, báo, cánh quạt chuyển động sẽ có động năng

a) Hai người chạy trên bờ biển

b) Sóng biển

c) Loài báo châu Phi săn mồi

d) Điện gió

- Mỗi liên hệ giữa động năng và công: \({W_d} - {W_{d0}} = \frac{1}{2}m{v^2} - \frac{1}{2}mv_0^2 = A\)

- Định lí động năng: độ biến thiên động năng của một vật trong khoảng thời gian Δt bằng công của lực tác dụng lên vật trong khoảng thời gian đó.

b. Đặc điểm của động năng

- Động năng của vật phụ thuộc vào khối lượng của vật và tốc độ chuyển động của vật

- Động năng là một đại lượng vô hướng, không âm

- Động năng có giá trị phụ thuộc vào hệ quy chiếu

a. Thế năng trong trường trọng lực đều

- Ví dụ:

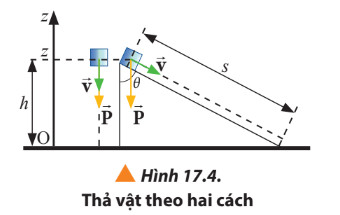
Một vật có khối lượng m ở độ cao h so với một vị trí làm gốc dự trữ một dạng năng lượng được gọi là thế năng trọng trường: Wt = m.g.h

Trong hệ SI, thế năng có đơn vị là joule (J)

- Ví dụ:

Búa máy đang dự trữ thế năng	Vận động viên nhảy cầu có thế năng và động năng

Lưu ý:

- Để xác định thế năng, ta cần phải chọn gốc thế năng là vị trí mà tại đó thế năng bằng 0.

- Khi chọn gốc tọa độ trùng với gốc thế năng và chiều dương của trục Oz hướng lên thì vị trí phía trên gốc thế năng có giá trị h > 0, vị trí phía dưới gốc thế năng có giá trị h < 0

- Độ biến thiên thế năng giữa hai vị trí không phụ thuộc vào việc chọn gốc thế năng.

b. Vận dụng công thức thế năng trọng trường

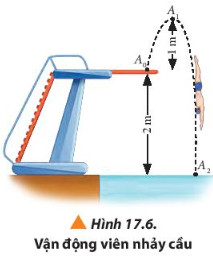
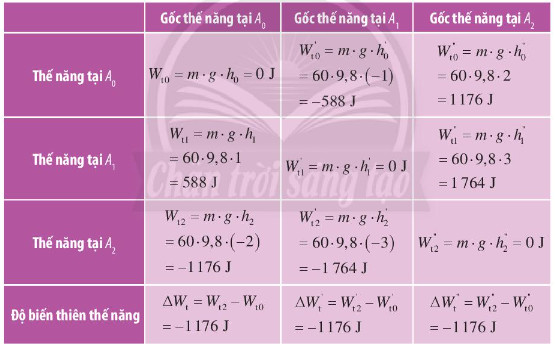
Ví dụ: Xét một vận động viên nhảy cầu có khối lượng 60 kg bắt đầu giậm nhảy từ cầu có độ cao 2 m so với mặt nước (Hình 17.6). Độ cao cực đại mà người này có thể đạt được là 1 m tính từ cầu nhảy. Lấy gia tốc trọng trường g = 9.8 m/s². Chọn chiều dương hướng lên và gốc thế năng lần lượt tại các vị trí A₀, A₁, và A₂)

a) Xác định thế năng trọng trường của vận động viên tại các vị trí A₀, A₁, và A₂

b) Xác định độ biến thiên thế năng từ khi vận động viên này giậm nhảy đến khi chạm mặt nước.

Hướng dẫn giải:

Gọi thế năng tại A₀, A₁, và A₂ lần lượt là W_t0, W_t1, và W_t2. Chọn chiểu dương thẳng đứng hướng lên. Thế năng tại các điểm đang xét và độ biến thiên thế năng giữa hai điểm A₂ và A₀ được cho ở bảng dưới đây.

a. Quá trình chuyển hóa giữa động năng và thế năng

Trong quá trình chuyển động, động năng và thế năng của vật có thể chuyển hóa quá lại với nhau.

Ví dụ:

Động năng và thế năng trong quá trình người trượt nước, quả bóng bay vào rổ chuyển hóa qua lại với nhau

+ Chọn gốc thế năng trọng trường tại chân đường trượt nước (Hình 17.7a) và tại mặt đất (Hình 17.7b).

+ Đường trượt nước: Người chơi phải đi cầu thang lên đến đỉnh của đường trượt nước ở một độ cao nhất định, sau đó dùng ván để trượt từ trên cao xuống. Khi này, động năng của người chơi tăng trong khi thế năng của họ giảm.

+ Môn bóng rổ: Trong môn thể thao này, để ghi điểm, vận động viên phải ném được quả bóng lên cao và rơi vào rổ. Khi bóng bay lên, động năng của bóng giảm trong khi thế năng của bóng tăng. Khi bóng rơi xuống, động năng của bóng tăng trong khi thế năng của bóng giảm.

b. Định luật bảo toàn cơ năng

- Tổng động năng và thế năng được gọi là cơ năng của vật: \({\rm{W}} = {{\rm{W}}_d} + {{\rm{W}}_t}\) - Khi một vật chuyển động chỉ chịu tác dụng của lực bảo toàn thì cơ năng của vật là một đại lượng bảo toàn.

- Trong hệ SI, cơ năng có đơn vị là jun (J)

- Ví dụ:

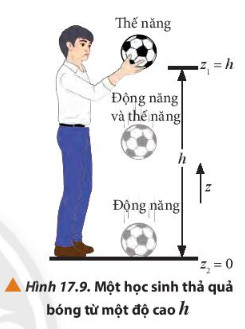
- Hệ quả: Trong trường trọng lực, tại vị trí vật có động năng cực đại thì thế năng cực tiểu và ngược lại.

c. Vận dụng định luật bảo toàn cơ năng

Ví dụ: Một thiết bị được thả không vận tốc đầu xuống bể mặt của Mặt Trăng, biết rằng gia tốc rơi tự do tại bể mặt của Mặt Trăng là 1,62 m/s². Muốn thiết bị được an toàn thì tốc độ khi tiếp đất của thiết bị đó phải nhỏ hơn 2 m/s. Xác định độ cao cần thiết để thả thiết bị được an toàn.

Hướng dẫn giải:

Chọn gốc thế năng tại bề mặt của Mặt Trăng.

Tại vị trí thả thiết bị, cơ năng của vật chính là thế năng:

W₁ = W_đ1 + W_t1 = m.g.h

Tại bề mặt của Mặt Trăng, cơ năng của vật chính là động năng:

\({W_2} = {\rm{ }}{W_{2}} + {\rm{ }}{W_{t2}} = {\rm{ }}\frac{1}{2}m{v^2}\)

Vì thiết bị chỉ chịu tác dụng của trọng lực do Mặt Trăng sinh ra (lực bảo toàn) nên cơ năng của thiết bị được bảo toàn: W₁ = W₂

Do đó, ta có: \(v = \sqrt {2g.h} \)

Để thiết bị được an toàn thì \(v \le 2m/s \Rightarrow h \le 1,23m\)

Vậy phải thả rơi thiết bị ở độ cao nhỏ hơn 1,23 m

Bài tập 1: Từ độ cao 180 m người ta thả rơi một vật nặng không vận tốc ban đầu. Bỏ qua sức cản không khí. Lấy g=10 m/s². Chọn gốc thế năng tại mặt đất. Khi thế năng bằng động năng thì vật có độ cao h và vận tốc v. Giá trị \(\frac{h}{v}\) gần giá trị nào sau đây nhất?

Hướng dẫn giải:

Gọi A là điểm thả vật, B là điểm có độ cao h và vận tốc v.

Theo định luật bảo toàn cơ năng:

\({{\rm{W}}_A} = {{\rm{W}}_B} \Leftrightarrow m.g.{h_A} + \frac{1}{2}.m.\nu _A^2 = m.g.{h_B} + \frac{1}{2}.m.\nu _B^2\)

Mà theo bài ra: \(m.g.{h_B} = \frac{1}{2}.m.\nu _B^2\)

Suy ra: \(m.g.{h_B} = \frac{1}{2}.m.\nu _B^2 = \frac{1}{2}.m.g.{h_A}\)

\(\Rightarrow \left\{ \begin{array}{l}
{h_B} = \frac{1}{2}.{h_A} = 90(m)\\
{v_B} = \sqrt {g.hA}  = 30\sqrt 2 (m/s)
\end{array} \right. \Rightarrow \frac{{{h_B}}}{{{v_B}}} = 2,12\)

Bài tập 2: Một vật có khối lượng 10 kg, lấy g=10 m/s2. Tính thế năng trọng trường của vật tại đáy giếng cách mặt đất 5 m với gốc thế năng tại mặt đất.

Hướng dẫn giải:

Áp dụng công thức tính thế năng trọng trường của vật ta có:

 \({{\rm{W}}_t} = m.g.h = 10.10.\left( { - 5} \right) =  - 500\left( J \right)\) (do mốc tính thế năng ở mặt đất).

Bài tập 3: Một viên đạn có khối lượng 14 g bay theo phương ngang với vận tốc 400 m/s xuyên qua tấm gỗ dày 5 cm, sau khi xuyên qua gỗ, đạn có vận tốc 120 m/s. Tính lực cản trung bình của tấm gỗ tác dụng lên viên đạn.

Hướng dẫn giải:

Xét theo phương ngang, áp dụng định lí động năng ta có:

\(\begin{array}{l}
\Delta {{\rm{W}}_d} = A \Leftrightarrow \frac{1}{2}.m.{\nu ^2} - \frac{1}{2}.m.\nu _0^2 = {A_c}\\
 \Rightarrow \frac{1}{2}{.14.10^{ - 3}}\left( {{{120}^2} - {{400}^2}} \right) = {F_c}{.5.10^{ - 2}}{\rm{cos18}}{{\rm{0}}^0}\\
 \Rightarrow Fc = 20384(N)
\end{array}\)

Sau bài học này, học sinh sẽ nắm được:

- Động năng và thế năng

- Cơ năng và định luật bảo toàn cơ năng

Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Vật Lý 10 Chân trời sáng tạo Chương 6 Bài 17 cực hay có đáp án và lời giải chi tiết. 

Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức về bài học này nhé!

Các em có thể xem thêm phần hướng dẫn Giải bài tập Vật Lý 10 Chân trời sáng tạo Chương 6 Bài 17 để giúp các em nắm vững bài học và các phương pháp giải bài tập.

Mở đầu trang 105 SGK Vật Lý 10 Chân trời sáng tạo - CTST

Câu hỏi thảo luận 1 trang 105 SGK Vật Lý 10 Chân trời sáng tạo - CTST

Câu hỏi thảo luận 2 trang 105 SGK Vật Lý 10 Chân trời sáng tạo - CTST

Luyện tập trang 106 SGK Vật Lý 10 Chân trời sáng tạo - CTST

Câu hỏi thảo luận 3 trang 106 SGK Vật Lý 10 Chân trời sáng tạo - CTST

Vận dụng trang 106 SGK Vật Lý 10 Chân trời sáng tạo - CTST

Câu hỏi thảo luận 4 trang 107 SGK Vật Lý 10 Chân trời sáng tạo - CTST

Câu hỏi thảo luận 5 trang 107 SGK Vật Lý 10 Chân trời sáng tạo - CTST

Luyện tập trang 108 SGK Vật Lý 10 Chân trời sáng tạo - CTST

Câu hỏi thảo luận 6 trang 109 SGK Vật Lý 10 Chân trời sáng tạo - CTST

Luyện tập trang 109 SGK Vật Lý 10 Chân trời sáng tạo - CTST

Vận dụng trang 109 SGK Vật Lý 10 Chân trời sáng tạo - CTST

Câu hỏi thảo luận 7 trang 110 SGK Vật Lý 10 Chân trời sáng tạo - CTST

Luyện tập trang 111 SGK Vật Lý 10 Chân trời sáng tạo - CTST

Vận dụng trang 111 SGK Vật Lý 10 Chân trời sáng tạo - CTST

Giải bài tập 1 trang 112 SGK Vật Lý 10 Chân trời sáng tạo - CTST

Giải bài tập 2 trang 112 SGK Vật Lý 10 Chân trời sáng tạo - CTST

Giải bài tập 3 trang 112 SGK Vật Lý 10 Chân trời sáng tạo - CTST

Giải bài tập 4 trang 112 SGK Vật Lý 10 Chân trời sáng tạo - CTST

Giải bài tập trắc nghiệm 17.1 trang 54 SBT Vật lý 10 Chân trời sáng tạo - CTST

Giải bài tập trắc nghiệm 17.2 trang 54 SBT Vật lý 10 Chân trời sáng tạo - CTST

Giải bài tập trắc nghiệm 17.3 trang 54 SBT Vật lý 10 Chân trời sáng tạo - CTST

Giải bài tập trắc nghiệm 17.4 trang 54 SBT Vật lý 10 Chân trời sáng tạo - CTST

Giải bài tập trắc nghiệm 17.5 trang 54 SBT Vật lý 10 Chân trời sáng tạo - CTST

Giải bài tập trắc nghiệm 17.6 trang 55 SBT Vật lý 10 Chân trời sáng tạo - CTST

Giải bài tập trắc nghiệm 17.7 trang 55 SBT Vật lý 10 Chân trời sáng tạo - CTST

Giải bài tập trắc nghiệm 17.8 trang 55 SBT Vật lý 10 Chân trời sáng tạo - CTST

Giải bài tập trắc nghiệm 17.9 trang 55 SBT Vật lý 10 Chân trời sáng tạo - CTST

Giải bài tập trắc nghiệm 17.10 trang 56 SBT Vật lý 10 Chân trời sáng tạo - CTST

Giải bài tập tự luận 17.1 trang 56 SBT Vật lý 10 Chân trời sáng tạo - CTST

Giải bài tập tự luận 17.2 trang 56 SBT Vật lý 10 Chân trời sáng tạo - CTST

Giải bài tập tự luận 17.3 trang 56 SBT Vật lý 10 Chân trời sáng tạo - CTST

Giải bài tập tự luận 17.4 trang 56 SBT Vật lý 10 Chân trời sáng tạo - CTST

Giải bài tập tự luận 17.5 trang 57 SBT Vật lý 10 Chân trời sáng tạo - CTST

Giải bài tập tự luận 17.6 trang 57 SBT Vật lý 10 Chân trời sáng tạo - CTST

Giải bài tập tự luận 17.7 trang 57 SBT Vật lý 10 Chân trời sáng tạo - CTST

Giải bài tập tự luận 17.8 trang 57 SBT Vật lý 10 Chân trời sáng tạo - CTST

Giải bài tập tự luận 17.9 trang 57 SBT Vật lý 10 Chân trời sáng tạo - CTST

Giải bài tập tự luận 17.10 trang 57 SBT Vật lý 10 Chân trời sáng tạo - CTST

Giải bài tập tự luận 17.11 trang 57 SBT Vật lý 10 Chân trời sáng tạo - CTST

Giải bài tập tự luận 17.12 trang 58 SBT Vật lý 10 Chân trời sáng tạo - CTST

Giải bài tập tự luận 17.13 trang 58 SBT Vật lý 10 Chân trời sáng tạo - CTST

Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Vật lý HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!

Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!