Xin giới thiệu với các em Phương pháp giải điện thế, hiệu điện thế, mối liên hệ giữa cường độ điện trường và hiệu điện thế môn Vật lý 11 năm học 2021 - 2022 do HOC247 biên soạn nhằm ôn tập và củng cố các kiến thức về chương Điện tích - Điện trường trong chương trình Vật Lý lớp 11 năm học 2020. Mời các em tham khảo tại đây!
1. PHƯƠNG PHÁP GIẢI
- Điện thế tại điểm M trong điện trường được xác định bởi
\({{V}_{M}}=\frac{{{W}_{M}}}{q}=\frac{{{A}_{M\infty }}}{q}\)
(điện thế tại vô cùng bằng 0, \({{V}_{\infty }}=0\))
- Hiệu điện thế \({{U}_{MN}}\) giữa hai điểm M và N là đại lượng đặc trưng cho khả năng sinh công của điện trường trong sự di chuyển của điện tích q từ M đến N.
\({{U}_{MN}}={{V}_{M}}-{{V}_{N}}=\frac{{{A}_{MN}}}{q}\)
2. VÍ DỤ MINH HỌA
Ví dụ 1: Tam giác ABC vuông tại A được đặt trong điện trường đều \(\overrightarrow{E}\), \(\alpha =\widehat{ABC}=60{}^\circ ,\,\,\overrightarrow{AB}\uparrow \uparrow \overrightarrow{E}\) (hình vẽ). Biết \(BC=6cm\), hiệu điện thế \({{U}_{BC}}=120V\).
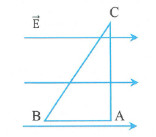
a) Tìm \({{U}_{AC}},\,\,{{U}_{BA}}\) và cường độ điện trường E?
A. \({{U}_{AC}}=0,\,\,{{U}_{BC}}=120V,\,\,E=4000V/m\)
B. \({{U}_{AC}}=120\,V,\,\,{{U}_{BC}}=0,\,\,E=4000V/m.\)
C. \({{U}_{AC}}=0,\,\,{{U}_{BC}}=-120\,V,\,\,E=2000V/m.\)
D. \({{U}_{AC}}=0,\,\,{{U}_{BC}}=120\,V,\,\,E=2000V/m.\)
b) Đặt thêm ở C điện tích điểm \(q={{9.10}^{-10}}C\). Tìm cường độ điện trường tổng hợp tại A?
A. 5000 V/m.
B. 2500 V/m.
C. 3000 V/m.
D. 4500 V/m.
Hướng dẫn giải
a) Vì \(\overrightarrow{AB}\uparrow \uparrow \overrightarrow{{{E}_{1}}}\) nên ta sẽ chiếu lên AB.
Ta có \(\overrightarrow{AC}\) vuông góc với AB nên hình chiếu bằng 0, suy ra \({{U}_{AC}}=0\)
Ta có \({{d}_{BC}}=\overline{{B}'{C}'}=BA\) nên ta có
\({{U}_{BC}}=E.BA={{U}_{BA}}=120V,\,\,E=\frac{{{U}_{BA}}}{BA}=\frac{120}{\frac{BC}{2}}=\frac{120}{0,03}=4000\left( V/m \right)\)
Đáp án A.
b) Cường độ điện trường do điện tích q gây ra tại A:
\({{E}_{1}}=\frac{kq}{A{{C}^{2}}}=\frac{kq}{\left( BC.\sin 60{}^\circ \right)}=3000\left( V/m \right)\)
Cường độ điện trường tổng hợp gây ra ở A là \(\overrightarrow{{{E}_{A}}}=\overrightarrow{E}+\overrightarrow{{{E}_{1}}}\), vì 2 vectơ này vuông góc với nhau nên
\(\Rightarrow {{E}_{A}}=\sqrt{{{E}^{2}}+E_{1}^{2}}=\sqrt{{{3000}^{2}}+{{4000}^{2}}}=5000\left( V/m \right)\)
Đáp án A.
Ví dụ 2: Cho 3 bản kim loại phẳng A, B, C có tích điện và đặt song song như hình. Cho \({{d}_{1}}=5cm,\,\,{{d}_{2}}=8cm\). Coi điện trường giữa các bản là đều và có chiều như hình vẽ. Cường độ điện trường tương ứng là \({{E}_{1}}={{4.10}^{4}}V/m,\,\,{{E}_{2}}={{5.10}^{4}}V/m\). Tính điện thế của bản B và bản C nếu lấy gốc điện thế là điện thế bản A.
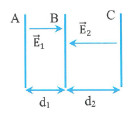
A. \({{V}_{B}}=-2000V,\,\,{{V}_{C}}=2000V.\)
B. \({{V}_{B}}=2000V,\,\,{{V}_{C}}=-2000V.\)
C. \({{V}_{B}}=-1200V,\,\,{{V}_{C}}=1600V.\)
D. \({{V}_{B}}=1200V,\,\,{{V}_{C}}=-1600V.\)
Hướng dẫn giải
Nếu M, N không nằm trên đường sức, khi đó công thức tính hiệu điện thế sẽ là:
\({{U}_{MN}}=Ed\cos \alpha \), trong đó \(\alpha =\left( \overrightarrow{MN},\overrightarrow{E} \right)\)
Vì lấy gốc điện thế tại bản A nên \({{V}_{A}}=0\)
\({{U}_{AB}}={{E}_{1}}.{{d}_{1}}=0,{{05.4.10}^{4}}=2000V=-{{V}_{B}}\)
Từ đó suy ra \({{V}_{B}}=-2000V\)
Ta có \({{U}_{AC}}={{U}_{AB}}+{{U}_{BC}}=2000-{{E}_{2}}{{d}_{2}}=2000-{{5.10}^{4}}.0,08=-2000V={{V}_{A}}-{{V}_{C}}\)
Mà \({{V}_{A}}=0\) nên từ đó suy ra \({{V}_{C}}=2000V\).
Đáp án A
Ví dụ 3: Giữa hai điểm B và C cách nhau một đoạn 0,2m có một điện trường đều với đường sức hướng từ \(B\to C\). Hiệu điện thế \({{U}_{BC}}=12V\). Tìm:
a) Cường độ điện trường giữa B và C.
A. 30 V/m.
B. 60 V/m.
C. 90 V/m.
D. 45 V/m.
b) Công của lực điện khi một điện tích \(q=+{{2.10}^{-6}}C\) đi từ B đến C.
A. \({{A}_{BC}}=24\mu J\).
B. \({{A}_{BC}}=12\mu J\)
C. \({{A}_{BC}}=-24\mu J\)
D. \({{A}_{BC}}=-12\mu J\).
Hướng dẫn giải
a) Ta có \({{U}_{BC}}=E.BC.\cos \alpha \) và đường sức hướng từ \(B\to C\) nên
\(\overrightarrow{BC}\uparrow \uparrow \overrightarrow{E}\Rightarrow \cos \alpha =\cos 0=1\)
Cường độ điện trường giữa B và C
\({{E}_{BC}}=\frac{{{U}_{BC}}}{BC}=\frac{12}{0,2}=60\left( V/m \right)\)
Đáp án B.
b) Công của lực điện khi một điện tích \(q={{2.10}^{-6}}C\) đi từ B đến C là
\({{A}_{BC}}=q.{{U}_{BC}}={{24.10}^{-6}}J=24\mu J\)
Đáp án A.
Ví dụ 4: Ba điểm A, B, C tạo thành một tam giác vuông tại C. \(AC=4cm,\,\,BC=3cm\) và nằm trong một điện trường đều. Vectơ cường độ điện trường \(\overrightarrow{E}\) song song với AC, hướng từ \(A\to C\) và có độ lớn \(E=5000V/m\). Tính:
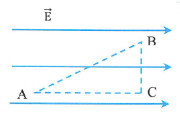
a) \({{U}_{AC}},\,\,{{U}_{CB}},\,\,{{U}_{AB}}\).
A. \({{U}_{AC}}=200\left( V \right),\,\,{{U}_{CB}}=0\left( V \right),\,\,{{U}_{AB}}=200\left( V \right)\).
B. \({{U}_{AC}}=-200\left( V \right),\,\,{{U}_{CB}}=0\left( V \right),\,\,{{U}_{AB}}=200\left( V \right)\).
C. \({{U}_{AC}}=200\left( V \right),\,\,{{U}_{CB}}=0\left( V \right),\,\,{{U}_{AB}}=-200\left( V \right)\).
D. \({{U}_{AC}}=-200\left( V \right),\,\,{{U}_{CB}}=0\left( V \right),\,\,{{U}_{AB}}=-200\left( V \right)\).
b) Công của điện trường khi một electron (e) di chuyển từ A đến B?
A. \({{A}_{e}}=-3,{{2.10}^{-17}}\left( J \right)\)
B. \({{A}_{e}}=-1,{{6.10}^{-17}}\left( J \right)\)
C. \({{A}_{e}}=3,{{2.10}^{-17}}\left( J \right)\)
D. \({{A}_{e}}=1,{{6.10}^{-17}}\left( J \right)\)
Hướng dẫn giải
a)
\(\left\{ \begin{align} & {{U}_{AC}}=E.AC=5000.0,04=200V \\ & {{U}_{CB}}=0 \\ & {{U}_{AB}}=E.AC={{U}_{AC}}=200V \\ \end{align} \right.\)
Đáp án A.
b) Công của điện trường khi một electron (e) di chuyển từ A đến B
\({{A}_{e}}=q.E.AC=-1,{{6.10}^{-19}}.5000.0,04=-3,{{2.10}^{-17}}J\)
Đáp án A.
Ví dụ 5: Ba điểm A, B, C nằm trong điện trường đều sao cho \(\overrightarrow{E}\parallel CA\). Cho \(AB\bot AC\) và \(AB=6cm,\,\,AC=8cm\).
a) Tính cường độ điện trường \(E,\,\,{{U}_{AB}}\) và \({{U}_{BC}}\). Biết \({{U}_{CD}}=100V\) (D là trung điểm của AC)
A. \(E=2500\left( V/m \right),\,\,{{U}_{AB}}=0V,\,\,{{U}_{BC}}=200V\)
B. \(E=2500\left( V/m \right),\,\,{{U}_{AB}}=0V,\,\,{{U}_{BC}}=-200V\)
C. \(E=1250\left( V/m \right),\,\,{{U}_{AB}}=0V,\,\,{{U}_{BC}}=-200V\)
D. \(E=1250\left( V/m \right),\,\,{{U}_{AB}}=0V,\,\,{{U}_{BC}}=200V\)
b) Tính công của lực điện trường khi electron di chuyển từ \(B\to C\), từ \(B\to D\)
A. \({{A}_{BC}}=-3,{{2.10}^{-17}}J,\,\,{{A}_{BD}}=1,{{6.10}^{-17}}\)
B. \({{A}_{BC}}=3,{{2.10}^{-17}}J,\,\,{{A}_{BD}}=-1,{{6.10}^{-17}}\)
C. \({{A}_{BC}}=3,{{2.10}^{-17}}J,\,\,{{A}_{BD}}=1,{{6.10}^{-17}}\).
D. \({{A}_{BC}}=-3,{{2.10}^{-17}}J,\,\,{{A}_{BD}}=-1,{{6.10}^{-17}}\)
Hướng dẫn giải
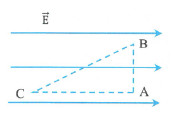
a) Hiệu điện thế giữa hai điểm C và D là
\({{U}_{CD}}=E.CD=\frac{E.CA}{2}\Rightarrow E=\frac{2{{U}_{CD}}}{CA}=2500\left( V/m \right)\)
Hiệu điện thế giữa hai điểm A và B. \(\overrightarrow{AB}\) vuông góc với \(\overrightarrow{E}\) nên \({{U}_{AB}}=0V\)
Hiệu điện thế giữa hai điểm B và C
\({{U}_{BC}}=-E.CA=-2500.0,08=-200V\)
Đáp án B.
b) Công của lực điện trường khi electron di chuyển từ \(B\to C\)
\({{A}_{BC}}=-eE.AC=1,{{6.10}^{-19}}.2500.0,08=3,{{2.10}^{-17}}J\)
Công của lực điện trường khi electron di chuyển từ \(B\to D\)
\({{A}_{BD}}={{A}_{AD}}=\frac{1}{2}{{A}_{BC}}=1,{{6.10}^{-17}}J\)
Đáp án C.
3. LUYỆN TẬP
Câu 1: Công thức xác định công của lực điện trường làm dịch chuyển điện tích q trong điện trường đều E là A = qEd, trong đó d là:
A. khoảng cách giữa điểm đầu và điểm cuối.
B. khoảng cách giữa hình chiếu điểm đầu và hình chiếu điểm cuối lên một đường sức.
C. độ dài đại số của đoạn từ hình chiếu điểm đầu đến hình chiếu điểm cuối lên một đường sức, tính theo chiều đường sức điện.
D. độ dài đại số của đoạn từ hình chiếu điểm đầu đến hình chiếu điểm cuối lên một đường sức.
Câu 2: Phát biểu nào sau đây là không đúng?
A. Công của lực điện tác dụng lên một điện tích không phụ thuộc vào dạng đường đi của điện tích mà chỉ phụ thuộc vào vị trí điểm đầu và điểm cuối của đoạn đường đi trong điện trường.
B. Hiệu điện thế giữa hai điểm trong điện trường là đại lượng đặc trưng cho khả năng sinh công của điện trường làm dịch chuyển điện tích giữa hai điểm đó.
C. Hiệu điện thế giữa hai điểm trong điện trường là đại lượng đặc trưng cho điện trường tác dụng lực mạnh hay yếu khi đặt điện tích thử tại hai điểm đó.
D. Điện trường tĩnh là một trường thế.
Câu 3: Mối liên hệ giữa hiệu điện thế \({{U}_{MN}}\) và hiệu điện thế \({{U}_{NM}}\) là:
A. \({{U}_{MN}}={{U}_{NM}}\).
B. \({{U}_{MN}}=-{{U}_{NM}}\).
C. \({{U}_{MN}}=\frac{1}{{{U}_{NM}}}\).
D. \({{U}_{MN}}=-\frac{1}{{{U}_{NM}}}\).
Câu 4: Hai điểm M và N nằm trên cùng một đường sức của một điện trường đều có cường độ E, hiệu điện thế giữa M và N là \({{U}_{MN}}\), khoảng cách MN=d. Công thức nào sau đây là không đúng?
A. \({{U}_{MN}}={{V}_{M}}-{{V}_{N}}\)
B. \({{U}_{MN}}=E.d\)
C. \({{A}_{MN}}=q.{{U}_{MN}}\)
D. \(E={{U}_{MN}}.d\)
Câu 5: Một điện tích q chuyển động trong điện trường không đều theo một đường cong kín. Gọi công của lực điện trong chuyển động đó là A thì
A. \(A>0\) nếu \(q>0\)
B. \(A>0\) nếu \(q<0\)
C. \(A\ne 0\) còn dấu của A chưa xác định vì chưa biết chiều chuyển động của q.
D. A=0 trong mọi trường hợp.
Câu 6: Hai tấm kim loại song song, cách nhau 2 (cm) và được nhiễm điện trái dấu nhau. Muốn làm cho điện tích \(q={{5.10}^{-10}}\left( C \right)\) di chuyển từ tấm này đến tấm kia cần tốn một công \(A={{2.10}^{-9}}\left( J \right)\). Coi điện trường bên trong khoảng giữa hai tấm kim loại là điện trường đều và có các đường sức điện vuông góc với các tâm. Cường độ điện trường bên trong tấm kim loại đó là:
A. \(E=2\left( V/m \right)\).
B. \(E=40\left( V/m \right)\).
C. \(E=200\left( V/m \right)\).
D. \(E=400\left( V/m \right)\).
Câu 7: Một electron chuyển động dọc theo đường sức của một điện trường đều. Cường độ điện trường \(E=100\left( V/m \right)\). Vận tốc ban đầu của electron bằng 300 (km/s). Khối lượng của electron là \(m=9,{{1.10}^{-31}}\left( kg \right)\). Từ lúc bắt đầu chuyển động đến lúc vận tốc của electron bằng không thì electron chuyển động được quãng đường là:
A. \(S=5,12\left( mm \right)\).
B. \(S=2,56\left( mm \right)\).
C. \(S=5,{{12.10}^{-3}}\left( mm \right)\).
D. \(S=2,{{56.10}^{-3}}\left( mm \right)\).
Câu 8: Hiệu điện thế giữa hai điểm M và N là \({{U}_{MN}}=1\left( V \right)\). Công của điện trường làm dịch chuyển điện tích \(q=-1\left( \mu C \right)\) từ M đến N là:
A. \(A=-1\left( \mu J \right)\).
B. \(A=+1\left( \mu J \right)\).
C. \(A=-1\left( J \right)\).
D. \(A=+1\left( J \right)\).
Câu 9: Một quả cầu nhỏ khối lượng \(3,{{06.10}^{-15}}\left( kg \right)\), mang điện tích \(4,{{8.10}^{-18}}\left( C \right)\), nằm lơ lửng giữa hai tấm kim loại song song nằm ngang nhiễm điện trái dấu, cách nhau một khoảng 2 (cm). Lấy \(g=10\left( m/{{s}^{2}} \right)\). Hiệu điện thế đặt vào hai tấm kim loại đó là:
A. \(U=255,0\left( V \right)\)
B. \(U=127,5\left( V \right)\)
C. \(U=63,75\left( V \right)\)
D. \(U=734,4\left( V \right)\)
Câu 10: Công của lực điện trường làm di chuyển một điện tích giữa hai điểm có hiệu điện thế \(U=2000\left( V \right)\) là \(A=1\left( J \right)\). Độ lớn của điện tích đó là
A. \(q={{2.10}^{-4}}\left( C \right)\).
B. \(q={{2.10}^{-4}}\left( \mu C \right)\).
C. \(q={{5.10}^{-4}}\left( C \right)\).
D. \(q={{5.10}^{-4}}\left( \mu C \right)\).
Câu 11: Một điện tích \(q=1\left( \mu C \right)\) di chuyển từ điểm A đến điểm B trong điện trường, nó thu được một năng lượng \(W=0,2\left( mJ \right)\). Hiệu điện thế giữa hai điểm A, B là:
A. \(U=0,20\left( V \right)\)
B. \(U=0,20\left( mV \right)\)
C. \(U=200\left( kV \right)\)
D. \(U=200\left( V \right)\)
Câu 12: Một điện trường đều cường độ 4000 V/m, có phương song song với cạnh huyền BC của một tam giác vuông ABC có chiều từ B đến C, biết \(AB=6cm,\,\,AC=8cm\). Tính hiệu điện thế giữa hai điểm BC:
A. 400V
B. 300V
C. 200V
D. 100V
Câu 13: Một điện tích q chuyển động từ điểm M đến Q, đến N, đến P trong điện trường đều như hình vẽ. Đáp án nào là sai khi nói về mối quan hệ giữa công của lực điện trường dịch chuyển điện tích trên các đoạn đường:
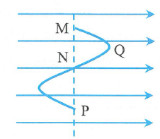
A. \({{A}_{MQ}}=-{{A}_{QN}}\)
B. \({{A}_{MN}}={{A}_{NP}}\)
C. \({{A}_{QP}}={{A}_{QN}}\)
D. \({{A}_{MQ}}={{A}_{MP}}\)
Câu 14: Hai tấm kim loại phẳng song song cách nhau 2cm nhiễm điện trái dấu. Muốn làm cho điện tích \(q={{5.10}^{-10}}C\) di chuyển từ tấm này sang tấm kia cần tốn một công \(A={{2.10}^{-9}}J\). Xác định cường độ điện trường bên trong hai tấm kim loại, biết điện trường bên trong là điện trường đều có đường sức vuông góc với các tấm, không đổi theo thời gian:
A. 100 V/m
B. 200 V/m
C. 300 V/m
D. 400 V/m
Câu 15: Hiệu điện thế giữa hai điểm M, N là \({{U}_{MN}}=2V\). Một điện tích q=-1C di chuyển từ M đến N thì công của lực điện trường là:
A. -2J
B. 2J
C. -0,5J
D. 0,5J
Câu 16: Một hạt bụi khối lượng \(3,{{6.10}^{-15}}kg\) mang điện tích \(q=4,{{8.10}^{-18}}C\) nằm lơ lửng giữa hai tấm kim loại phẳng song song nằm ngang cách nhau 1cm và nhiễm điện trái dấu. Lấy \(g=10m/{{s}^{2}}\), tính hiệu điện thế giữa hai tấm kim loại:
A. 25V
B. 50V
C. 75V
D. 100V
Câu 17: Một quả cầu kim loại khối lượng \(4,{{5.10}^{-3}}kg\) treo vào đầu một sợi đây dài 1m, quả cầu nằm giữa hai tấm kim loại phẳng song song thẳng đứng cách nhau 4cm, đặt hiệu điện thế giữa hai tấm là 750V, thì quả cầu lệch 1cm ra khỏi vị trí ban đầu và lệch về phía tấm tích điện dương, lấy \(g=10m/{{s}^{2}}\). Tính điện tích của quả cầu:
A. 24nC
B. -24nC
C. 48nC
D. -36nC
Câu 18: Giả thiết rằng một tia sét có điện tích q=25C được phóng từ đám mây dông xuống mặt đất, khi đó hiệu điện thế giữa đám mây và mặt đất \(U=1,{{4.10}^{8}}V\). Tính năng lượng của tia sét đó:
A. \({{35.10}^{8}}J\)
B. \({{45.10}^{8}}J\)
C. \({{55.10}^{8}}J\)
D. \({{65.10}^{8}}J\)
Câu 19: Một điện tích điểm \(q=+10\mu C\) chuyển động từ đỉnh B đến đỉnh C của tam giác đều ABC, nằm trong điện trường đều có cường độ 5000 V/m có đường sức điện trường song song với cạnh BC có chiều từ C đến B. Biết cạnh tam giác bằng 10cm, tìm công của lực điện trường khi di chuyển điện tích trên theo đoạn thẳng B đến C:
A. \(2,{{5.10}^{-4}}J\)
B. \(-2,{{5.10}^{-4}}J\)
C. \(-{{5.10}^{-4}}J\)
D. \({{5.10}^{-4}}J\)
Câu 20: Một điện tích điểm \(q=+10\mu C\) chuyển động từ đỉnh B đến đỉnh C của tam giác đều ABC, nằm trong điện trường đều có cường độ 5000 V/m có đường sức điện trường song song với cạnh BC có chiều từ C đến B. Biết cạnh tam giác bằng 10cm, tìm công của lực điện trường khi di chuyển điện tích trên theo đoạn gấp khúc BAC:
A. \(-{{10.10}^{-4}}J\)
B. \(-2,{{5.10}^{-4}}J\)
C. \(-{{5.10}^{-4}}J\)
D. \({{10.10}^{-4}}J\)
---(Để xem tiếp nội dung từ câu 11 đến câu 40 của tài liệu các em vui lòng xem Online hoặc Đăng nhập vào HOC247 để tải về máy)---
ĐÁP ÁN PHẦN LUYỆN TẬP
|
1-C |
2-C |
3-B |
4-D |
5-D |
6-C |
7-B |
8-A |
9-B |
10-C |
|
11-D |
12-A |
13-D |
14-B |
15-A |
16-C |
17-B |
18-A |
19-C |
20-C |
|
21-A |
22-D |
23-A |
24-D |
25-B |
26-C |
27-D |
28-B |
29-A |
30-C |
|
31-D |
32-A |
33-B |
34-D |
35-B |
36-A |
37-A |
38-C |
39-C |
40-A |
Trên đây là một phần trích đoạn nội dung Tài liệu Phương pháp giải điện thế, hiệu điện thế, mối liên hệ giữa cường độ điện trường và hiệu điện thế môn Vật lý 11 năm học 2021 - 2022. Để xem toàn bộ nội dung các em đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.
Hy vọng tài liệu này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong học tập.
Ngoài ra các em có thể tham khảo thêm một số tư liệu cùng chuyên mục sau:













