Phép biến hình và phép dời hình - Lê Bá Bảo

CHỦ ĐỀ 0: PHÉP BIẾN HÌNH VÀ PHÉP DỜI HÌNH

 

Để xem đầy đủ nội dung tài liệu các em có thể sử dụng chức năng xem Online hoặc đăng nhập Hoc247.net tải file PDF tài liệu về máy.

 

I- LÝ THUYẾT

1. Phép biến hình

a. Định nghĩa:

Phép biến hình là một quy tắc để với mỗi điểm M trong mặt phẳng xác định được với một điểm duy nhất \(M'\) của mặt phẳng và \(M'\): gọi là ảnh của M qua phép biến hình đó.

Ký hiệu: f là một phép biến hình nào đó và \(M'\) là ảnh của M qua f thì ta viết: \(M' = f\left( M \right)\) hay \(f\left( M \right) = M'\) hay \(f:M \mapsto M'\) hay M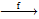M'.

Nhận xét:                    1) f là một phép biến hình đồng nhất \( \Leftrightarrow \forall M \in H:f\left( M \right) = M\)

(M được gọi là điểm bất động, kép, bất biến)

                                    2) \({f_1},{f_2}\) là các phép biến hình thì \({f_2}o{f_1},{f_1}o{f_2}\) là phép biến hình

                                    3) \(\left( {H'} \right)\) được gọi là ảnh của hình \(\left( H \right)\) qua phép biến hình f

                                    \( \Leftrightarrow \forall M \in \left( H \right):f\left( M \right) = M' \in \left( {H'} \right)\). Ta viết \(f\left( H \right) = H'\).

2. Phép dời hình

Định nghĩa: Phép dời hình là phép biến hình không làm thay đổi khoảng cách giữa hai điểm bất kỳ M, N và ảnh \(M',N'\) của chúng.

\(\forall M,N \in H:\left\{ \begin{array}{l}f\left( M \right) = M'\\f\left( N \right) = N'\end{array} \right. \Leftrightarrow MN = M'N'\)

3. Tính chất (của phép dời hình)

3.1- Phép dời hình biến 3 điểm thẳng hàng thành 3 điểm thẳng hàng, 3 điểm không thẳng hàng thành 3 điểm không thẳng hàng

3.2- Phép dời hình biến:

- Đường thẳng thành đường thẳng, tia thành tia, đoạn thẳng thành đoạn thẳng bằng nó

- Tam giác thành tam giác bằng nó (trực tâm \( \to \) trực tâm, trọng tâm \( \to \) trọng tâm)

- Đường tròn thành đường tròn bằng nó (tâm biến thành tâm: \(\left\{ \begin{array}{l}I \to I'\\R = R'\end{array} \right.\))

- Góc thành góc bằng nó

II- LUYỆN TẬP:

Dưới đây, là một số kỹ năng cơ bản giúp độc giả giải quyết xuyên suốt các vấn đề về các phép biến hình cụ thể được học.

Bài tập 1: Trong mặt phẳng tọa độ Oxy, chứng tỏ các quy tắc sau là một phép biến hình: a) Phép biến hình \({F_1}\) biến mỗi điểm \(M\left( {x;y} \right)\) thành điểm \(M'\left( {y; - x} \right)\) b) Phép biến hình \({F_2}\) biến mỗi điểm \(M\left( {x;y} \right)\) thành điểm \(M'\left( {2x;y} \right)\)

Gợi ý: Chỉ rõ: \(\forall M:\exists !M' = F\left( M \right)\)

a) Gọi \(M\left( {{x_M};{y_M}} \right)\)

* Theo quy tắc đặt như trên, luôn tồn tại điểm \(M':F\left( M \right) = M'\left( {{y_M}; - {x_M}} \right)\)

Như vậy, với mọi điểm M thì luôn tại ảnh là \({M'}\).                                  (1)

* Giả sử, qua quy tắc đặt trên, điểm \(M\left( {{x_M};{y_M}} \right)\) có 2 ảnh là: \(M'\left( {x_M';y_M'} \right),N'\left( {x_N';y_N'} \right)\)

Lúc đó: \(\left\{ \begin{array}{l}y_M' = {y_M}\\y_M' =  - {x_M}\end{array} \right.\left( i \right)\) và \(\left\{ \begin{array}{l}y_N' = {y_M}\\y_N' =  - {x_M}\end{array} \right.(ii)\)

Từ (i) và (ii) dễ thấy: \({M'} \equiv {N'}\)                                                    (2)

Từ (1) và (2), kết luận: Quy tắc đặt trên là một phép biến hình.

b) Độc giả chứng minh tương tự.

Nhận xét: Để chỉ rõ một quy tắc đặt cho trước là một phép biến hình, cần chỉ rõ 2 điểm: Với mọi điểm M, luôn tồn tại ảnh của M qua quy tắc đặt tương ứng. Ảnh của M qua quy tắc đặt tương ứng đó là duy nhất.

Ngược lại, một trong 2 yêu cầu trên không được thỏa mãn thì quy tắc đặt không là phép biến hình.

 

Bài tập 2: Trong mặt phẳng tọa độ Oxy, phép biến hình nào sau đây là phép dời hình? a) Phép biến hình \({F_1}\) biến mỗi điểm \(M\left( {x;y} \right)\) thành điểm \(M'\left( {y; - x} \right)\) b) Phép biến hình \({F_2}\) biến mỗi điểm \(M\left( {x;y} \right)\) thành điểm \(M'\left( {2x;y} \right)\)

Gợi ý: Chỉ rõ: \(\forall M,N:F\left( M \right) = M',F\left( N \right) = N' \Rightarrow M'N' = MN\)

Lấy hai điểm \(M\left( {{x_1};{y_1}} \right),N\left( {{x_2};{y_2}} \right)\), ta có: \(MN = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \)

a) Ảnh của M, N qua phép biến hình \({F_1}\) lần lượt được \(M'\left( {{y_1}; - {x_1}} \right),N'\left( {{y_2}; - {x_2}} \right)\)

Ta có: \(M'N' = \sqrt {{{\left( {{y_2} - {y_1}} \right)}^2} + {{\left( {{x_1} - {x_2}} \right)}^2}}  = MN\)

Vậy phép biến hình \({F_1}\) là phép dời hình.

b) Tương tự,

Xét ảnh của M, N qua phép biến hình \({F_2}\) lần lượt được \(M'\left( {2{x_1};{y_1}} \right),N'\left( {2{x_2};{y_2}} \right)\).

Ta có: \(M'N' = \sqrt {2{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \)

Để ý rằng, nếu \({x_1} \ne {x_2}\) thì \({M'}{N'} \ne MN\).

Kết luận: Phép biến hình \({F_2}\) không là phép dời hình.

 

Bài tập 3: Trong mặt phẳng tọa độ Oxy, với \(\alpha ,a,b\) là những số cho trước. Xét phép biến hình F biến mỗi điểm \(M\left( {x;y} \right)\) thành điểm \(M'\left( {x';y'} \right)\), trong đó: \(\left\{ \begin{array}{l}x' = x\cos \alpha  - ysin\alpha  + a\\y' = x\sin \alpha  + y\cos \alpha  + b\end{array} \right.\) a) Chứng minh: F là phép dời hình b) Khi \(\alpha  = 0\). Chứng minh: F là phép tịnh tiến.

Gợi ý: Chỉ rõ: \(\forall M,N:F\left( M \right) = M',F\left( N \right) = N' \Rightarrow M'N' = MN\)

a) Phép biến hình F biến \(M\left( {{x_1};{y_1}} \right),N\left( {{x_2};{y_2}} \right)\) tương ứng thành \(M'\left( {x_1';y_1'} \right),N'\left( {x_2';y_2'} \right)\), với:

\(\left\{ \begin{array}{l}x_1' = {x_1}\cos \alpha  - {y_1}\sin \alpha  + a\\y_1' = {x_1}\sin \alpha  + {y_1}\cos \alpha  + b\end{array} \right.\) và \(\left\{ \begin{array}{l}x_2' = {x_2}\cos \alpha  - {y_2}\sin \alpha  + a\\y_2'= {x_2}\sin \alpha  + {y_2}\cos \alpha  + b\end{array} \right.\)

Ta có: \(MN = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \)

Xét: \(M'N' = \sqrt {{{\left( {x_2' - x_1'} \right)}^2} + {{\left( {y_2^/ - y_1'} \right)}^2}} \)

\(\begin{array}{l} = \sqrt {{{\left[ {\left( {{x_2} - {x_1}} \right)\cos \alpha  - \left( {{y_2} - {y_1}} \right)\sin \alpha } \right]}^2} + {{\left[ {\left( {{x_2} - {x_1}} \right)\sin \alpha  + \left( {{y_2} - {y_1}} \right)\cos \alpha } \right]}^2}} \\ = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\cos }^2}\alpha  + {{\left( {{y_2} - {y_1}} \right)}^2}{{\sin }^2}\alpha  + {{\left( {{x_2} - {x_1}} \right)}^2}{{\sin }^2}\alpha  + {{\left( {{y_2} - {y_1}} \right)}^2}{{\cos }^2}\alpha } \\ = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2}\left( {{{\cos }^2}\alpha  + {{\sin }^2}\alpha } \right) + {{\left( {{y_2} - {y_1}} \right)}^2}\left( {{{\cos }^2}\alpha  + {{\sin }^2}\alpha } \right)} \\ = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}  = MN\end{array}\)

Kết luận: Vậy phép biến hình F là phép dời hình.

b) Khi \(\alpha  = 0\), ta có: \(\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\)

Hay: \(M(x;y)\)\(M'(x+a;y+b)\) 

Vậy F là phép tịnh tiến theo vecto \(\overrightarrow v  = \left( {a;b} \right).\)

 

{--Xem đầy đủ nội dung ở phần xem Online hoặc tải về--}

Hy vọng tài liệu này sẽ trở thành một nguồn tham khảo bổ ích cho các em trong quá trình học tập.

Chúc các em học tốt và đạt kết quả cao trong các kì thi!