Đề thi học kỳ 1 môn Toán lớp 10 năm 2017 sau đây gồm trắc nghiệm và tự luận có đáp án sẽ giúp các em học sinh có thêm tài liệu tham khảo chuẩn bị thật tốt cho bài thi học kỳ 1 sắp tới.
SỞ GD & ĐT THÁI BÌNH
TRƯỜNG THPT QUỲNH CÔI ( Đề thi có 03 trang) |
ĐỀ KIỂM TRA CHẤT LƯỢNG HỌC KỲ MỘT LỚP 10 NĂM HỌC 2017-2018 Môn: TOÁN Thời gian làm bài: 90 phút, không kể thời gian phát đề |
Mã đề: 061
I. PHẦN TRẮC NGHIỆM (6,0 điểm)
Câu 1: Cho đồ thị hàm số \(y = a{x^2} + bx + c\) có hình bên. Khẳng định nào sau đây đúng?
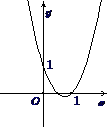
A. \(a > 0,\,\,b < 0,\,\,c > 0\) B. \(a > 0,\,\,b > 0,\,\,c > 0\)
C. \(a > 0,\,\,b < 0,\,\,c < 0\) D. \(a < 0,\,\,b < 0,\,\,c > 0\)
Câu 2: Cho phương trình \(2x - \frac{3}{x} = {x^2} - \frac{3}{x}\)(1). Phương trình nào sau đây tương đương với phương trình (1) ?
A. \(2x = {x^2}\) B. \( - \frac{3}{x} = {x^2} - 2{\rm{x}} - \frac{3}{x}\)
C. \({\left( {2x - \frac{3}{x}} \right)^2} = {\left( {{x^2} - \frac{3}{x}} \right)^2}\) D. \(2{x^2} - 3 = {x^3} - 3\)
Câu 3: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với trọng tâm G. Biết rằng \(A\left( {1\,\,;\,\, - 2} \right),$$B\left( {5\,\,;0} \right),G\left( {2\,\,;\,\,1} \right)\). Tìm tọa độ C?
A. \(C\left( {0\,\,;\,\,5} \right)\) B.\(C\left( {0\,\,;\,\, - 1} \right)\) C.\(C\left( {\frac{8}{3}\,\,;\frac{{ - 1}}{3}} \right)\) D. \(D\left( {8\,\,;5} \right)\)
Câu 4: Cho tam giác ABC đều cạnh a, Gọi G là trọng tâm tam giác ABC. Đẳng thức nào dưới đây sai ?
A.\(\left| {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right| = 0\) B. \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = a\sqrt 3 \)
C. \(\left| {\overrightarrow {AB} - \overrightarrow {AC} } \right| = a\) D. \(\left| {\overrightarrow {GB} + \overrightarrow {GC} } \right| = a\)
Câu 5: Cho phương trình \(\left| {2x - 4} \right| = x - 1\), tích các nghiệm của phương trình là ?
A. 5 B. 4 C. 0 D. Một giá trị khác
Câu 6: Cho hình bình hành ABCD. Gọi I là trung điểm của CD,G là trọng tâm tam giác BCI. Đặt \(\overrightarrow a = \overrightarrow {AB,} \overrightarrow b = \overrightarrow {AD} \). Hãy tìm đẳng thức đúng trong các đẳng thức sau ?
A. \(\overrightarrow {AG} = \frac{5}{6}\overrightarrow a + \frac{2}{3}\overrightarrow b \) B. \(\overrightarrow {AG} = \frac{5}{6}\overrightarrow a + \overrightarrow b \) C. \(\overrightarrow {AG} = \overrightarrow a + \frac{5}{6}\overrightarrow b \) D. \(\overrightarrow {AG} = \frac{4}{3}\overrightarrow a + \frac{2}{3}\overrightarrow b \)
Câu 7: Tổng các nghiệm của phương trình \({\rm{2}}{{\rm{x}}^2} - {\rm{5}}\sqrt {2{x^2} - 1} + 3 = 0\) là ?
A. -3 B. 2 C. -1 D. 0
Câu 8: Cho hình chữ nhật ABCD thỏa mãn \(AB = 2BC = 2a\) khi đó \(\left| {\overrightarrow {AB} + \overrightarrow {A{\rm{D}}} } \right| = \)?
A. \(a\sqrt 5 \) B. \(a\sqrt 3 \) C. 3a D. 2a
Câu 9: Hàm số nào trong các hàm số sau không phải là hàm số lẻ ?
A. y = \(\sqrt {x + 1} \) B. \(y=x\) C. y = \(x\left| x \right|\) D. y = \(\frac{2}{{{x^3}}}\)
Câu 10: Cho hàm số \(y = f(x) = \frac{4}{{\sqrt {x + 1} }}\) có đồ thị là (C). Điểm nào dưới đây không thuộc (C) ?
A. \(Q\left( {15;1} \right)\) B. \(M\left( {3;2} \right)\) C. \(P\left( {0;4} \right)\) D. \(N\left( {1;0} \right)\)
----Để xem tiếp nội dung vui lòng xem online hoặc tải về----
Trên đây là phần trích dẫn đề thi học kỳ 1 môn Toán lớp 10. Để xem chi tiết nội dung đề thi, quý thầy cô cùng các em học sinh có thể chọn chức năng xem trực tuyến hoặc tài về máy. Ngoài ra, quý thầy cô và các em học sinh có thể tham khảo thêm một số đề thi khác tại website Hoc247.net







