Phương pháp tìm hàm số trùng phương khi biết đồ thị hàm số

Quan sát dáng đồ thị, chú ý các hệ số a >0; a<0.

Chú ý điểm cực trị:

\(ab < 0\): hàm số có 3 điểm cực trị;

\(ab \ge 0\) : hàm số có 1 điểm cực trị

Các giao điểm đặc biệt với trục Ox, Oy.

c>0: giao điểm trục tung nằm trên 0

c<0: giao điểm trục tung nằm dưới 0

c=0: giao điểm trục trùng với 0

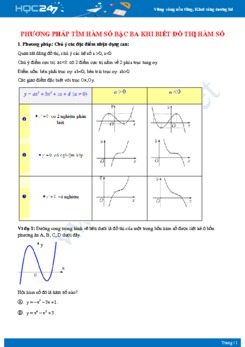
Ví dụ 1: Đường cong trong hình vẽ bên là đồ thị của hàm số nào trong các hàm số sau:

Ⓐ.\(y = \frac{{x - 2}}{{x + 1}}\). 

Ⓑ.\(y = {x^4} - 2{x^2} - 2\).

Ⓒ. \(y = - {x^4} + 2{x^2} - 2\). 

Ⓓ. \(y = {x^3} - 2{x^2} - 2\).

Lời giải

Chọn B

Đồ thị trên là đồ thị của hàm trùng phương có hệ số \(a\) dương nên từ các phương án đã cho ta suy ra đồ thị trên là đồ thị của hàm số \(y = {x^4} - 2{x^2} - 2\)

Ví dụ 2: Đồ thị sau đây là của hàm số nào?

Ⓐ.\(y = {x^4} + 2{x^2} - 3\). 

Ⓑ.\(y = {x^4} - 3{x^2} - 3\).

Ⓒ. \(y = {x^4} - 2{x^2} - 3\). 

Ⓓ. \(y = - \frac{1}{4}{x^4} + 3{x^2} - 3\).

Lời giải

Chọn C

Đồ thị có:\(\mathop {\lim }\limits_{x \to + \infty } y = + \infty\) \(\Rightarrow\) D sai.

Hàm số có các điểm cực trị là: \(x = 0\), \(x = \pm 1\)

\(\Rightarrow\) A, B sai.

Ví dụ 3: Đồ thị sau đây là đồ thị của hàm số nào?

Ⓐ.\(y = - {x^4} + 2{x^2} + 1\) 

Ⓑ.\(y = - {x^4} + 2{x^2}\).

Ⓒ. \(y = {x^4} - 2{x^2}\). 

Ⓓ. \(y = {x^4} - 2{x^2} + 1\).

Lời giải

Chọn B

Dựa vào đồ thị ta thấy \(a < 0,\,\,c = 0\)

Nên chỉ có đáp án B thỏa mãn.

Câu 1: Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây?

A. \(y = {x^4} - 2{x^2} + 2\). 

B. \(y = {x^2} + 2\).

C. \(y = - {x^4} + 2{x^2} + 2\). 

D. \(y = {x^3} - 3{x^2} + 2\).

Lời giải

Chọn A

Phân tích: Ta thấy đường cong dạng chữ W.

Từ đây ta loại C.

Tiếp tục với A và B ta xét xem \({y_B}\) có nằm phía trên trục hoành hay không.

Ta nhẩm nhanh: Với A thì phương trình \(y'=0\) có nghiệm \(x = \pm 1\) khi đó \(y\left( 1 \right) = 2\).

Câu 2: Đường cong trong hình vẽ bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi đó là hàm số nào?

A. \(y = - {x^3} + {x^2} - 2\). 

B. \(y = - {x^4} + 3{x^2} - 2\).

C. \(y = {x^4} - 2{x^2} - 3\). 

D. \(y = - {x^2} + x - 1\).

Lời giải

Chọn C

Đồ thị đi qua \(M\left( {0;\, - 3} \right)\), suy ra loại các phương án A, B, D.

Câu 3: Đường cong trong hình vẽ sau là đồ thị hàm số nào dưới đây?

A. \(y = - {x^4} + 4{x^2} + 1\). 

B. \(y = {x^3} + 3x + 1\). 

C. \(y = - {x^3} + 2{x^2} + 1\). 

D. \(y = {x^4} - 4{x^2} + 1\).

Lời giải

Chọn A

Nhận thấy đây là đồ thị hàm bậc bốn trùng phương nên loại B và C.

\(\left\{ {\begin{array}{*{20}{l}} {\mathop {\lim }\limits_{x \to \pm \infty } y = \mathop {\lim }\limits_{x \to \pm \infty } \left( { - {x^4} + 4{x^2} + 1} \right) = - \infty \left( N \right)}\\ {\mathop {\lim }\limits_{x \to \pm \infty } y = \mathop {\lim }\limits_{x \to \pm \infty } \left( {{x^4} + 4{x^2} + 1} \right) = + \infty \left( L \right)} \end{array}} \right.\)

Câu 4: Cho hàm số \(y = a{x^4} + b{x^2} + c\) có đồ thị như hình bên. Mệnh đề nào dưới đây là đúng?

A. \(a > 0,b < 0,c > 0\) 

B. \(a > 0,b < 0,c < 0\) 

C. \(a > 0,b > 0,c < 0\) 

D. \(a < 0,b > 0,c < 0\)

Lời giải

Chọn B

Ta có đồ thị có hình dạng như trên với hàm bậc bốn trùng phương có hai điểm cực tiểu và một điểm cực đại nên \(a > 0,b < 0\). Giá trị cực đại nhỏ hơn 0 nên \(c < 0\).

Câu 5: Đường cong trong hình vẽ sau là đồ thị của một hàm số trong các phương án A, B, C, D cho dưới đây. Hàm số đó là hàm số nào?

A. \(y = - {x^3} + 3{x^2} + 2\). 

B. \(y = 2{x^3} - 3{x^2} + 1\).

C. \(y = - {x^4} + 3{x^2} + 2\). 

D. \(y = {x^4} - {x^2} - 1\).

Lời giải

Dạng đồ thị hàm trùng phương, nhìn đồ thị nhận xét được hệ số \(a > 0\) nên ta chọn D.

Câu 6: Đường cong trong hình bên dưới là đồ thị của hàm số nào dưới đây?

A. \(y = {x^4} - 2{x^2} + 2\) 

B. \(y = - {x^3} + 3{x^2} + 2\) 

C. \(y = - {x^4} + 2{x^2} + 2\) 

D. \(y = {x^3} - 3{x^2} + 2\)

Lời giải

Từ đồ thị và các phương án lựa chọn ta thấy, hình dạng trên là dạng đồ thị hàm số bậc 4 trùng phương có hệ số \(a < 0\). Do đó chỉ có phương án C thỏa mãn.

Câu 7: Đồ thị trong hình sau là của hàm số nào dưới đây?

A. \(y = - {x^2} + x - 1\). 

B. \(y = {x^3} - 3x + 1\). 

C. \(y = - {x^4} + 2{x^2} + 1\). 

D. \(y = {x^4} - 2{x^2}\).

Lời giải

Chọn D

Từ đồ thị đi qua gốc toạ độ \(O\left( {0;0} \right)\), ta chọn hàm số \(y = {x^4} - 2{x^2}\).

Câu 8: Cho hàm số \(y = a{x^4} + b{x^2} + c\) có đồ thị như hình bên dưới. Số điểm cực trị của hàm số đã cho là

A. 2. 

B. 0. 

C. 1. 

D. 3.

Lời giải

Chọn D

Số điểm cực trị của hàm số đã cho là 3

Câu 9: Biết hình dưới đây là đồ thị của một trong bốn hàm số sau, hỏi đó là đồ thị của hàm số nào?

A. \(y = {x^4} - 2{x^2}\). 

B. \(y = {x^4} - 2{x^2} + 1\). 

C. \(y = {x^4} + 2{x^2}\). 

D. \(y = - {x^4} + 2{x^2}\).

Lời giải

Dựa vào đồ thị ta thấy

Đồ thị có 3 điểm cực trị và đi qua gốc tọa độ O nên loại đáp án B, C.

Nhánh cuối là một đường đi lên nên \(a > 0\) \(\Rightarrow\) chọn đáp án A.

Câu 10: Trong các hình vẽ sau, hình nào biểu diễn đồ thị của hàm số \(y = - {x^4} + 2{x^2} + 3\).

A.

B.

C.

D.

Lời giải

Chọn C

Vì hệ số \(a = - 1 < 0\) nên loại A, D.

Ta có: \(y'=-4{{x}^{3}}+4x\).

\(y'=0\Leftrightarrow \left[ \begin{array}{*{35}{l}} x=1 \\ x=-1 \\ x=0 \\ \end{array} \right.\)

Do đó hàm số có ba cực trị.

...

--(Nội dung đầy đủ, chi tiết vui lòng xem tại online hoặc đăng nhập để tải về máy)--

Trên đây là một phần trích đoạn nội dung Phương pháp tìm hàm số trùng phương khi biết đồ thị hàm số. Để xem thêm nhiều tài liệu tham khảo hữu ích khác các em chọn chức năng xem online hoặc đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.

Hy vọng tài liệu này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong học tập.

Các em quan tâm có thể tham khảo thêm các tài liệu cùng chuyên mục:

• Phương pháp tìm hàm số bậc ba khi biết đồ thị hàm số

• Phương pháp tìm hàm số hữu tỉ khi biết đồ thị hàm số

Chúc các em học tốt!