Giải bài 5 tr 83 sách BT Toán lớp 8 Tập 2
Cho tam giác ABC. Từ điểm D trên cạnh BC, kẻ các đường thẳng song song với các cạnh AB và AC, chúng cắt các cạnh AC và AB theo thứ tự tại F và E (hình dưới)
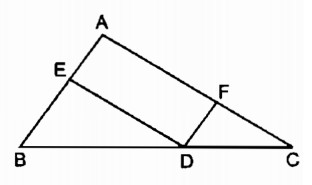
Chứng minh rằng :
\({{AE} \over {AB}} + {{AF} \over {AC}} = 1\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng định lí Ta - lét: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết
Xét \(∆ ABC\) có \(DE // AC\) (gt)
Theo định lí Ta-lét ta có:
\(\displaystyle {{AE} \over {AB}} = {{CD} \over {CB}}\) (1)
Lại có: \(DF // AB\) (gt)
Theo định lí Ta-lét ta có:
\(\displaystyle{{AF} \over {AC}} = {{BD} \over {BC}}\) (2)
Cộng (1) và (2) theo vế với vế, ta có:
\(\displaystyle {{AE} \over {AB}} + {{AF} \over {AC}} = {{CD} \over {CB}} + {{BD} \over {BC}} \)
\(\displaystyle \Rightarrow {{AE} \over {AB}} + {{AF} \over {AC}} = {{CD + BD} \over {BC}} \)
\(\displaystyle \Rightarrow {{AE} \over {AB}} + {{AF} \over {AC}} = {{BC} \over {BC}} = 1\
-- Mod Toán 8 HỌC247
-


Tính độ dài các cạnh DB,DC,DE biết tam giác ABC vuông tại A biết AB=21cm. AC=28cm
bởi Hoàng My
 31/05/2019
31/05/2019
câu 1: cho ΔABC vuông tại A biết AB=21cm. AC=28cm. phấn giác AD( D thuộc BC). đường thẳng qua D song song BA cắt AC tại E a/ tính độ dài các cạnh DB,DC,DE b/ tính diện tích ΔADB, ΔACB
câu 2: cho ΔABC cân tại A phân giác góc B cắt AC tại D biết AB=15cm, BC= 10cm a/ tính AD,BC b/ đường vuông góc với BD tại B cắt đường thẳng AC kéo dài tại E. tính độ dài đoạn EC
Theo dõi (0) 1 Trả lời -


Chứng minh DE//BC từ đó suy ra hai tam giác đồng dạng
bởi Hy Vũ
 30/08/2019
30/08/2019
Cho tam giác ABC nhọn, có AB=12cm, AC=15cm. Trên AB và AC lấy điểm D và E sao cho AD=4cm, AE=5cm.
a) CM: DE//BC, tứ đó suy ra: \(\Delta ADE\sim\Delta ABC\)
b) Từ E kẻ EF//AB (F thuộc BC). Tứ giác BDEF là hình gì? Từ đó suy ra: \(\Delta CEF\sim\Delta EAD\)
c) Tính CF và FB khi biết BC=18cm?
Theo dõi (0) 1 Trả lời -


Tính độ dài EF biết DE=10cm
bởi Thuy Kim
 30/08/2019
30/08/2019
hthang ABCD (AB//CD) có AB =28cm, CD=70 , AD=35 vẽ 1 đường thẳng // vs 2 đáy cắt AD,BC theo thứ tự ở E và F tính độ dài EF biết DE=10 cm
Theo dõi (0) 1 Trả lời -


Xác định vị trí điểm E sao cho AE = CF
bởi bich thu
 30/08/2019
30/08/2019
cho tam giác ABC có AB=5cm; AC=9cm. kẻ đường thẳng song song vs BC, cắt AB,AC lần lượt tại E và F. xác định vị trí điểm E sao cho AE = CF
Theo dõi (0) 1 Trả lời -


Cho tứ giác ABCD. Đường thẳng qua A và song song với BC cắt BD ở E. Đường thẳng qua B và song song với AD cắt AC ở G . CM: EG//CD
Theo dõi (0) 1 Trả lời -


Chứng minh FG song song BC biết tam giác ABC nhọn, đường cao BD, CE
bởi Nguyễn Lê Thảo Trang
 31/05/2019
31/05/2019
Cho tam giác ABC nhọn, đường cao BD và CE. Qua D kẻ DF vuông góc AB, qua E kẻ EG vuông góc AC. CMR:
A. AD. AE=AB.AG=AC.À
B. FG song song BC
Theo dõi (0) 1 Trả lời -


1, Cho hình thang ABCD (AB // CD), M là trung điểm của CD. Gọi I là giao điểm của AM và BD, K là giao điểm của BM và AC.
a, Chứng minh IK // AB.
b, Đường thẳng IK cắt AD, BC lần lượt ở E và F. CHứng minh EI = IK = KF.
Theo dõi (0) 1 Trả lời





