Mời các em cùng tham khảo bài Tứ giác mở đầu phần hình học Toán 8. Với bài học này, các em sẽ biết được các khái niệm, định lí về tứ giác và tứ giác lồi. Đây là một bài toán hình học căn bản giúp các em học tốt các phần tiếp theo. Chúc các em học tập thật tốt!
Tóm tắt lý thuyết
1.1. Tứ giác lồi
| Tứ giác ABCD là hình gồm bốn đoạn thẳng AB, BC , CD, DA trong đó không có hai đoạn thẳng nào nằm trên cùng một đoạn thẳng. |
Ví dụ 1: Hình a, b, c là tứ giác, hình d không phải là tứ giác.
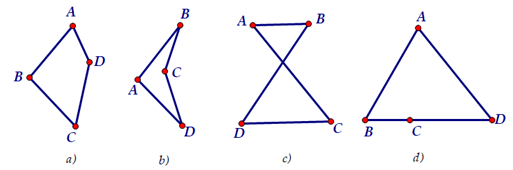
|
Trong tứ giác ABCD, các điểm A, B, C, D là các đỉnh, các đoạn thẳng AB, BC, CD, DA là các cạnh. - Tứ giác lồi là tứ giác mà hai đỉnh thuộc một cạnh bất kì luôn nằm về một phía của đường thẳng đi qua hai đỉnh còn lại. - Trong tứ giác lồi ABCD, các góc ABC, BCD, CDA, DAB gọi là các góc của tứ giác và kí hiệu đơn giản lần lượt là |
Chú ý:
- Từ nay, khi nói đến tứ giác mà không giải thích gì thêm, ta hiểu đó là tứ giác lồi.
- Tứ giác ABCD còn được gọi tên là tứ giác BCDA, CDAB, DABC, ADCB, DCBA, CBAD, BADC.
Ví dụ 2: Cho bốn điểm M, N, P, Q như hình, kể tên tứ giác có các đỉnh là bốn điểm đã cho.
Ta có: tứ giác MNPQ (hoặc NPQM, PQMN, QMNP, MQPN, QPNM, PNMQ, NMQP).
Ví dụ 3: Quan sát tứ giác MNPQ dưới đây. Ta có:
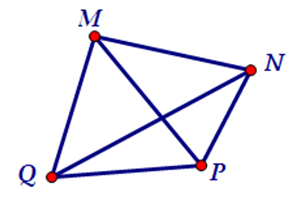
- Hai đỉnh không cùng thuộc một cạnh gọi là hai đỉnh đối nhau. Đoạn thẳng nối hai đỉnh đối nhau là một đường chéo, có hai đường chéo là MP và NQ.
- Cặp cạnh MN, PQ và MQ, NP là các cặp cạnh đối.
- Cặp góc M, P và N, Q là các cặp góc đối.
1.2. Tổng các góc của một tứ giác
| Định lí: Tổng các góc trong một tứ giác bằng 360° |
Ví dụ 4: Cho tứ giác MNPQ như hình bên, hãy tính góc M.
Hướng dẫn giải: Vì MN⊥NP và MQ⊥QP nên \(\hat{N}=\hat{Q}={{90}^{o}}\)
Theo định lí về tổng các góc trong một tứ giác ta có:
Do đó
Vậy
Bài tập minh họa
Bài 1. Tính góc chưa biết của các tứ giác trong hình sau:
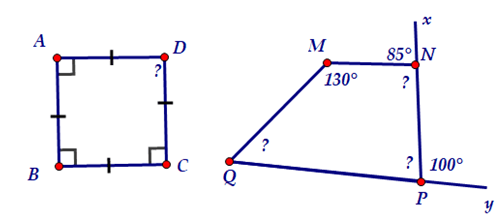
Hướng dẫn giải
- Tứ giác ABCD có 3 góc vuông nên . Theo ĐL về tổng các góc trong một tứ giác:
Suy ra
- Vì (hai góc kề bù)
(hai góc kề bù)
Theo định lí về tổng các góc trong một tứ giác ta có:
Suy ra
Bài 2. Tính góc chưa biết của tứ giác trong hình dưới đây, biết .
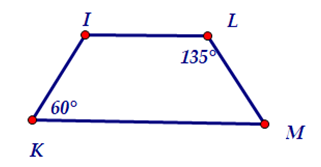
Hướng dẫn giải
- Vì mà
- Theo ĐL về tổng các góc trong một tứ giác ta có:
\(\begin{align} & =360{}^\circ -\left( 120{}^\circ +60{}^\circ +135{}^\circ \right) \\ & =45{}^\circ \\ \end{align}\)
3. Luyện tập Bài 10 Toán 8 Tập 1 - Kết nối tri thức
Qua bài học này, các em sẽ hoàn thành một số mục tiêu như sau:
- Mô tả được khái niệm tứ giác, tứ giác lồi.
- Giải thích được định lí về tổng các góc trong một tứ giác lồi.
3.1 Trắc nghiệm Bài 10 Toán 8 Tập 1 - Kết nối tri thức
Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Toán 8 Kết nối tri thức Bài 10 cực hay có đáp án và lời giải chi tiết.
-
Câu 1:
Các góc của tứ giác có thể là?
- A. 4 góc nhọn
- B. 4 góc tù
- C. 4 góc vuông
- D. 1 góc vuông, 3 góc nhọn
-
- A. Hai đỉnh kề nhau: A và B, A và D.
- B. Hai đỉnh đối nhau: A và C, B và D.
- C. Đường chéo: AC, BD.
- D. Các điểm nằm trong tứ giác là E, F và điểm nằm ngoài tứ giác là H.
-
Câu 3:
Hãy chọn câu sai trong các câu sau?
- A. Tứ giác lồi là tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kỳ cạnh nào của tứ giác.
- B. Tổng các góc của một tứ giác bằng 1800.
- C. Tổng các góc của một tứ giác bằng 3600.
- D. Tứ giác ABCD là hình gồm đoạn thẳng AB, BC, CD, DA, trong đó bất kì hai đoạn thẳng nào cũng không nằm trên một đường thẳng.
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!
3.2. Bài tập SGK Bài 10 Toán 8 Tập 1 - Kết nối tri thức
Các em có thể xem thêm phần hướng dẫn Giải bài tập Toán 8 Kết nối tri thức Bài 10 để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Mở đầu trang 48 SGK Toán 8 Kết nối tri thức tập 1 - KNTT
Câu hỏi trang 49 SGK Toán 8 Kết nối tri thức tập 1 - KNTT
Luyện tập 1 trang 49 SGK Toán 8 Kết nối tri thức tập 1 - KNTT
Hoạt động trang 50 SGK Toán 8 Kết nối tri thức tập 1 - KNTT
Luyện tập 2 trang 50 SGK Toán 8 Kết nối tri thức tập 1 - KNTT
Vận dụng trang 50 SGK Toán 8 Kết nối tri thức tập 1 - KNTT
Thử thách nhỏ trang 50 SGK Toán 8 Kết nối tri thức tập 1 - KNTT
Bài 3.1 trang 51 SGK Toán 8 Kết nối tri thức tập 1 - KNTT
Bài 3.2 trang 51 SGK Toán 8 Kết nối tri thức tập 1 - KNTT
Bài 3.3 trang 51 SGK Toán 8 Kết nối tri thức tập 1 - KNTT
Bài tập 3.1 trang 32 SBT Toán 8 Tập 1 Kết nối tri thức - KNTT
Bài tập 3.2 trang 32 SBT Toán 8 Tập 1 Kết nối tri thức - KNTT
Bài tập 3.3 trang 32 SBT Toán 8 Tập 1 Kết nối tri thức - KNTT
Bài tập 3.4 trang 32 SBT Toán 8 Tập 1 Kết nối tri thức - KNTT
Bài tập 3.5 trang 32 SBT Toán 8 Tập 1 Kết nối tri thức - KNTT
Bài tập 3.6 trang 32 SBT Toán 8 Tập 1 Kết nối tri thức - KNTT
4. Hỏi đáp Bài 10 Toán 8 Tập 1 - Kết nối tri thức
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Toán Học 8 HỌC247


.png)









