Bài tập 3.3 trang 32 SBT Toán 8 Tập 1 Kết nối tri thức
Chứng minh tổng độ dài hai đường chéo của tứ giác:
a) Bé hơn chu vi của tứ giác;
b) Lớn hơn tổng hai cạnh đối tuỳ ý của tứ giác, từ đó lớn hơn nửa chu vi của tứ giác.
Hướng dẫn giải chi tiết Bài tập 3.3
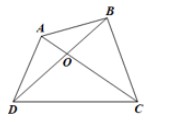
Xét tứ giác ABCD. Chu vi tứ giác ABCD là PABCD = AB + BC + CD + DA.
a) Trong ∆ABC có AC < AB + BC (bất đẳng thức trong tam giác)
Trong ∆ACD có AC < CD + DA (bất đẳng thức trong tam giác)
Do đó AC + AC < AB + BC + CD + DA hay 2AC < PABCD (1)
Tương tự, trong ∆ABD có BD < AD + AB
Trong ∆BCD có: BD < CD + BC
Do đó BD + BD < AD + AB + CD + BC hay 2BD < PABCD. (2)
Từ (1) và (2) suy ra 2(AC + BD) < 2PABCD, do đó AC + BD < PABCD.
b) Gọi O là giao điểm của AC và BD.
Trong ∆OAB có OA + OB > AB (bất đẳng thức trong tam giác)
Trong ∆OCD có OC + OD > CD (bất đẳng thức trong tam giác)
Nên AC + BD = OA + OC + OB + OD > AB + CD.
Trong ∆OAD có OA + OD > AD (bất đẳng thức trong tam giác)
Trong ∆OBC có OB + OC > BC (bất đẳng thức trong tam giác)
Nên AC + BD = OA + OC + OB + OD > AD + BC.
Vậy 2(AC + BD) > AB + BC + CD + DA = PABCD
Tức là
-- Mod Toán 8 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Bài tập 3.1 trang 32 SBT Toán 8 Tập 1 Kết nối tri thức - KNTT
Bài tập 3.2 trang 32 SBT Toán 8 Tập 1 Kết nối tri thức - KNTT
Bài tập 3.4 trang 32 SBT Toán 8 Tập 1 Kết nối tri thức - KNTT
Bài tập 3.5 trang 32 SBT Toán 8 Tập 1 Kết nối tri thức - KNTT
Bài tập 3.6 trang 32 SBT Toán 8 Tập 1 Kết nối tri thức - KNTT





