HỌC247 xin giới thiệu đến các em học sinh lớp 6 Tập hợp các số nguyên. Bài giảng có lý thuyết được tóm tắt ngắn gọn và các bài tập minh hoạ kèm theo lời giải chi tiết cho các em tham khảo, rèn luyện kỹ năng giải Toán 6. Mời các em học sinh cùng tham khảo.
Tóm tắt lý thuyết
1.1. Làm quen với số nguyên âm
Số nguyên dương: \(1;2;3;4;...\) (Số tự nhiên khác 0)
Số nguyên âm: \(- 1; - 2; - 3; - 4;...\)(Ta thêm dấu “-” vào đằng trước các số nguyên dương)
- Tập hợp: \(\left\{ {...; - 3; - 2; - 1;0;1;2;3;...} \right\}\) gồm các số nguyên âm, số \(0\) và các số nguyên dương là tập hợp các số nguyên. Kí hiệu là \(\mathbb{Z} = \left\{ {...; - 3; - 2; - 1;0;1;2;3;...} \right\}\)
Chú ý:
- Số \(0\) không phải là số nguyên dương cũng không phải số nguyên âm.
- Đôi khi ta còn viết thêm dấu “+” ngay trước một số nguyên dương. Chẳng hạn \( + 5\) (đọc là “dương năm”)
Khi nào người ta dùng số âm?
- Trong đời sống hàng ngày người ta dùng các số mang dấu "-" và dấu "+" để chỉ các đại lượng có thể xét theo hai chiều khác nhau.
|
Số dương biểu thị |
Số âm biểu thị |
|
Nhiệt độ trên \({0^0}C\) |
Nhiệt độ dưới \({0^0}C\) |
|
Độ cao trên mực nước biển |
Độ cao dưới mực nước biển |
|
Số tiền hiện có |
Số tiền còn nợ |
|
Số tiền lãi |
Số tiền lỗ |
|
Độ viễn thị |
Độ cận thị |
Ví dụ:
+) Số \( - 1\) đọc là “âm một”.
+) Số +2 đọc là “dương hai”
+) Một người thợ lặn lặn xuống độ sâu 10 mét tức là độ cao hiện tại của người thợ lặn là -10m so với mực nước biển.
1.2. Thứ tự trên tập hợp số nguyên
a) Trục số
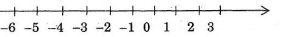
+ Trên trục số: Điểm \(0\)được gọi là điểm gốc của trục số. Chiều từ trái sang phải gọi là chiều dương (thường được đánh dấu bằng mũi tên), chiều từ phải sang trái gọi là chiều âm của trục số.
+ Điểm biểu diễn số nguyên \(a\) trên trục số gọi là điểm \(a.\)
+) Cho số nguyên \(a\) và \(b\). Trên trục số, nếu điểm \(a\) nằm bên trái điểm \(b\) thì số \(a\) nhỏ hơn số \(b\), kí hiệu \(a < b\)
Ví dụ:
Số 2 trên trục số được gọi là điểm 2.
Số \( - 9\) trên trục số được gọi là điểm \( - 9\)
Ví dụ: Cho trục số như hình vẽ.
.png)
Ta thấy điểm biểu diễ số \( - 5\) nằm bên trái điểm biểu diễn số \( - 3\) nên \( - 5 < - 3.\)
b) So sánh hai số nguyên
- Mọi số nguyên âm đều nhỏ hơn 0.
- Mọi số nguyên âm đều nhỏ hơn số nguyên dương.
- Mọi số nguyên dương đều lớn hơn 0.
- Nếu \(a,b\) là hai số nguyên dương và \(a > b\) thì \( - a < - b\) (Thêm dấu “-” thì đổi dấu “>” thành dấu “<”)
- Nếu \(a,b\) là hai số nguyên dương và \(a < b\) thì \( - a > - b\)
- Kí hiệu \(a \le b\) có nghĩa là “\(a < b\) hoặc \(a = b\)”
- Kí hiệu \(a \ge b\) có nghĩa là “\(a > b\) hoặc \(a = b\)”
Chú ý:
Để so sánh 2 số nguyên âm, ta làm 2 bước sau:
Bước 1: Bỏ dấu "-" trước cả 2 số âm
Bước 2: Trong 2 số nguyên dương nhận được, số nào nhỏ hơn thì số nguyên âm ban đầu( trước khi bỏ dấu "-" lớn hơn
Ví dụ:
5 là số nguyên dương và \( - 25\) là số nguyên âm nên \(5 > - 25\)
Vì \(15 > 3\) nên \( - 15 < - 3\)
Bài tập minh họa
Câu 1:
a) Viết ba số nguyên dương và ba số nguyên âm;
b) Đọc các số mà em đã viết.
Hướng dẫn giải
a) Ba số nguyên dương: 2, 7, 9
Ba số nguyên âm: - 3, - 5, - 6
b) 2: hai
7: bảy
9: chín
-3: âm ba
-5: âm năm
-6: âm sáu
Câu 2:
1.Sắp xếp các số sau theo thứ tự tăng dần 2, -4; 0; 5; -11; -3; 9.
2.Trong tập \({\rm{\{ }}x \in \mathbb{Z}| - 5 < x \le 2\} \) những số nào lớn hơn – 1?
Hướng dẫn giải
1. Sắp xếp các số theo thứ tự tăng dần: -11; -4; -3; 0; 2; 5; 9
2. Ta có: \({\rm{\{ }} - 4;\, - 3\,;\, - 2;\, - 1;\,\,0;\,\,1;\,\,2{\rm{\} }}\) nên
Những số lớn hơn -1 là: 0; 1; 2
Câu 3:
a. Sắp xếp các số nguyên sau theo thứ tự tăng dần: 5, -15, 8, 3, -1, 0
b. Sắp xếp các số nguyên sau theo thứ tự giảm dần: -97, 10, 0, 4, -9, 2000
Hướng dẫn giải
a. Thứ tự tăng dần: -15, -1, 0, 3, 5, 8
b. Thứ tự giảm dần: 2000, 10, 4, 0, -9, -97
Luyện tập Bài 13 Chương 3 Toán 6 KNTT
Qua bài giảng này giúp các em học được:
- Số nguyên âm là số như thế nào.
- Thứ tự trên tập hợp số nguyên
- Cách biểu diễn số nguyên âm trên trục số.
- Số đối của một số nguyên
- Vận dụng lý thuyết làm một số bài tập liên quan đến tập số nguyên
3.1. Bài tập tự luận về Tập hợp các số nguyên
Câu 1: Trên trục số, mỗi điểm sau nằm cách gốc O bao nhiêu đơn vị?
a) Điểm 2
b) Điểm -4
Câu 2: Tìm giá trị tuyệt đối của các số: 1998, -2001, -9
Câu 3: Tìm \(x \in Z\), biết rằng -4
3.2. Bài tập trắc nghiệm về Tập hợp các số nguyên
Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Toán 6 Kết nối tri thức Chương 3 Bài 13 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.
-
- A. 3
- B. -3
- C. -4
- D. 4
-
- A. Nếu + 50 000 đồng biểu diễn số tiền có 50 000 đồng, thì – 50 000 đồng biểu diễn số tiền cho vay là 50 000 đồng.
- B. Số 0 là số nguyên dương.
- C. Số đối của số 0 là số 0.
- D. Số 0 là số nguyên âm.
-
- A. B = {-2; 0; -3; -6}
- B. B = {2; 0; 3; 6}
- C. B = {-6; -3; 0; 2}
- D. B = {-2; 0; 3; 6}
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!
3.3 Bài tập SGK về Tập hợp các số nguyên
Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Toán 6 Kết nối tri thức Chương 3 Bài 13 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK Toán 6 tập 1
Hoạt động 1 trang 58 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Hoạt động 2 trang 58 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Luyện tập 1 trang 58 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Giải câu hỏi 1 trang 59 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Vận dụng 1 trang 59 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Giải câu hỏi 2 trang 60 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Luyện tập 2 trang 60 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Hoạt động 3 trang 60 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Hoạt động 4 trang 60 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Luyện tập 3 trang 60 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Vận dụng 2 trang 60 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Tranh luận trang 61 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Giải bài 3.1 trang 61 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Giải bài 3.2 trang 61 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Giải bài 3.3 trang 61 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Giải bài 3.4 trang 61 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Giải bài 3.5 trang 61 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Giải bài 3.6 trang 61 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Giải bài 3.7 trang 61 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Giải bài 3.8 trang 61 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Giải bài 3.1 trang 48 SBT Toán 6 Kết nối tri thức tập 1 - KNTT
Giải bài 3.2 trang 48 SBT Toán 6 Kết nối tri thức tập 1 - KNTT
Giải bài 3.3 trang 49 SBT Toán 6 Kết nối tri thức tập 1 - KNTT
Giải bài 3.4 trang 49 SBT Toán 6 Kết nối tri thức tập 1 - KNTT
Giải bài 3.5 trang 49 SBT Toán 6 Kết nối tri thức tập 1 - KNTT
Giải bài 3.6 trang 49 SBT Toán 6 Kết nối tri thức tập 1 - KNTT
Giải bài 3.7 trang 49 SBT Toán 6 Kết nối tri thức tập 1 - KNTT
4. Hỏi đáp Bài 13 Chương 3 Toán 6 KNTT
Nếu có thắc mắc cần giải đáp các em có thể để lại câu hỏi trong phần Hỏi đáp, cộng đồng Toán HỌC247 sẽ sớm trả lời cho các em.
-- Mod Toán Học 6 HỌC247







