Thực hành 2 trang 85 SGK Toán 11 Chân trời sáng tạo tập 2
Cho hình chóp tứ giác đều \(S.ABCD\) với \(O\) là tâm của đáy và có tất cả các cạnh đều bằng \(a\). Xác định và tính góc phẳng nhị diện:
a) \(\left[ {S,BC,O} \right]\);
b) \(\left[ {C,SO,B} \right]\).
Hướng dẫn giải chi tiết Thực hành 2
Phương pháp giải:
‒ Cách xác định góc phẳng nhị diện \(\left[ {A,d,B} \right]\): Dựng mặt phẳng \(\left( P \right)\) vuông góc với \(d\), gọi \(a,a'\) lần lượt là giao tuyến của \(\left( P \right)\) với hai nửa mặt phẳng chứa \(A,B\), khi đó \(\left[ {A,d,B} \right] = \left( {a,a'} \right)\).
Lời giải chi tiết:
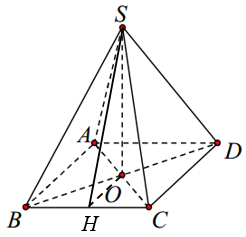
a) Gọi \(H\) là trung điểm của \(BC\).
\(\Delta SBC\) đều \( \Rightarrow SH \bot BC\)
\(\Delta OBC\) vuông cân tại \(O \Rightarrow OH \bot BC\)
Vậy \(\widehat {SHO}\) là góc phẳng nhị diện \(\left[ {S,BC,O} \right]\).
Ta có: \(O\) là trung điểm của \(BD\)
\(H\) là trung điểm của \(BC\)
\( \Rightarrow OH\) là đường trung bình của \(\Delta BC{\rm{D}}\)
\( \Rightarrow OH = \frac{1}{2}CD = \frac{a}{2}\)
\(AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \Rightarrow OC = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}\)
\(\Delta SOH\) vuông tại \(O\) có: \(SO = \sqrt {S{C^2} - O{C^2}} = \frac{{a\sqrt 2 }}{2}\)
\(\tan \widehat {SHO} = \frac{{SO}}{{OH}} = \sqrt 2 \Rightarrow \widehat {SHO} \approx 54,{7^ \circ }\)
b) Ta có:
\(\begin{array}{l}SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OB\\SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OC\end{array}\)
Vậy \(\widehat {BOC}\) là góc phẳng nhị diện \(\left[ {C,SO,B} \right]\).
\(ABC{\rm{D}}\) là hình vuông \( \Rightarrow \widehat {BOC} = {90^ \circ }\).
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Hoạt động khám phá 2 trang 84 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 3 trang 84 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Vận dụng 2 trang 85 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 1 trang 85 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 2 trang 85 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 3 trang 85 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 4 trang 85 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 5 trang 85 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Bài tập 1 trang 73 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 2 trang 73 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 3 trang 73 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 4 trang 73 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST





