Hoạt động khám phá 7 trang 118 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST

Phương pháp giải:

‒ Sử dụng định lí 3: Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) song song với nhau. Nếu \(\left( R \right)\) cắt \(\left( P \right)\) thì cắt \(\left( Q \right)\) và hai giao tuyến của chúng song song.

‒ Sử dụng tính chất của hình lăng trụ.

‒ Sử dụng tính chất của hình bình hành.

Lời giải chi tiết:

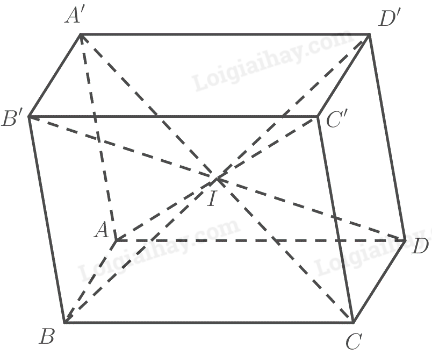
a) Vì \(ABCD.A'B'C'D'\) là hình lăng trụ nên có:

‒ Hai đáy \(ABCD\) và \(A'B'C'D'\) bằng nhau và là hình bình hành.

‒ Các mặt bên \(AA'B'B,AA'D'D,BB'C'C,CC'D'D\) là các hình bình hành.

b) Ta có:

\(\left. \begin{array}{l}\left( {ABC{\rm{D}}} \right)\parallel \left( {A'B'C'D'} \right)\\\left( {AA'C'C} \right) \cap \left( {ABC{\rm{D}}} \right) = AC\\\left( {AA'C'C} \right) \cap \left( {A'B'C'D'} \right) = A'C'\end{array} \right\} \Rightarrow AC\parallel A'C'\)

Mà \(AA'\) và \(CC'\) là các cạnh bên của hình lăng trụ nên \(AA'\parallel CC'\)

Vậy \(AA'C'C\) là hình bình hành.

\(\left. \begin{array}{l}\left( {ABC{\rm{D}}} \right)\parallel \left( {A'B'C'D'} \right)\\\left( {BB'D'D} \right) \cap \left( {ABC{\rm{D}}} \right) = B{\rm{D}}\\\left( {BB'D'D} \right) \cap \left( {A'B'C'D'} \right) = B'D'\end{array} \right\} \Rightarrow B{\rm{D}}\parallel B'D'\)

Mà \(BB'\) và \(DD'\) là các cạnh bên của hình lăng trụ nên \(BB'\parallel DD'\)

Vậy \(BB'D'D\) là hình bình hành.

c) Ta có:

\(\left. \begin{array}{l}\left( {ABC{\rm{D}}} \right)\parallel \left( {A'B'C'D'} \right)\\\left( {A'B'C{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right) = C{\rm{D}}\\\left( {A'B'C{\rm{D}}} \right) \cap \left( {A'B'C'D'} \right) = A'B'\end{array} \right\} \Rightarrow C{\rm{D}}\parallel A'B'\left( 1 \right)\)

\(ABC{\rm{D}}\) là hình bình hành nên \(AB = CD\)

\(AA'B'B\) là hình bình hành nên \(AB = A'B'\)

Vậy \(A'B' = CD\left( 2 \right)\)

Từ (1) và (2) suy ra \(A'B'C{\rm{D}}\) là hình bình hành

\( \Rightarrow A'C,B'D\) cắt nhau tại trung điểm của mỗi đường.

Chứng minh tương tự ta có:

+ \(ABC'D'\) là hình bình hành nên \(AC',B{\rm{D}}'\) cắt nhau tại trung điểm của mỗi đường

+ \(A'BCD'\) là hình bình hành nên \(A'C,B{\rm{D}}'\) cắt nhau tại trung điểm của mỗi đường

Do đó bốn đoạn thẳng \(A'C,AC',B'D,BD\) có cùng trung điểm.

-- Mod Toán 11 HỌC247