Bài tập 4 trang 128 SBT Toán 11 Tập 1 Chân trời sáng tạo
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và M, N lần lượt là trung điểm của AB, CD. (P) là mặt phẳng đi qua MN và song song với mặt phẳng (SAD). Tìm giao tuyến của các mặt của hình chóp với mặt phẳng (P)?
Hướng dẫn giải chi tiết Bài tập 4
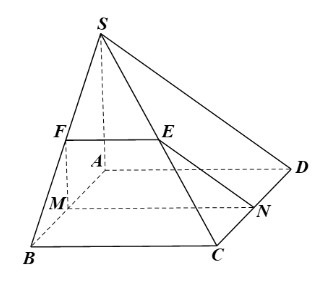
Do M, N lần lượt là trung điểm của AB, CD nên MN // BC // AD.
Mà AD ⊂ (SAD) nên MN // (SAD).
Gọi E là trung điểm của SC.
Xét ∆SCD có N, E lần lượt là trung điểm của CD, SC.
Nên NE là đường trung bình của tam giác, suy ra NE // SD.
Mà SD ⊂ (SAD) nên NE // (SAD).
Ta có: MN // (SAD);
NE // (SAD);
MN ∩ NE = N trong (MNE).
Do đó (MNE) // (SAD).
Khi đó (MNE) chính là mặt phẳng (P).
Gọi F là trung điểm của SB, tương tự ta cũng có (MNEF) là mặt phẳng (P).
Vậy, (P) ∩ (ABCD) = MN với MN // BC // AD.
(P) ∩ (SAB) = MF với MF // SA (F là trung điểm của SB).
(P) ∩ (SDC) = NE với NE // SD (E là trung điểm của SC).
(P) ∩ (SBC) = EF.
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





