Hoạt động khám phá 2 trang 102 SGK Toán 11 Chân trời sáng tạo tập 1
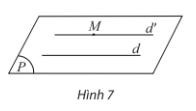
a) Trong không gian, cho điểm \(M\) ở ngoài đường thẳng \(d\). Đặt \(\left( P \right) = mp\left( {M,d} \right)\). Trong \(\left( P \right)\), qua \(M\) vẽ đường thẳng \(d'\) song song với \(d\), đặt \(\left( Q \right) = mp\left( {d,d'} \right)\). Có thể khẳng định hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) trùng nhau không?
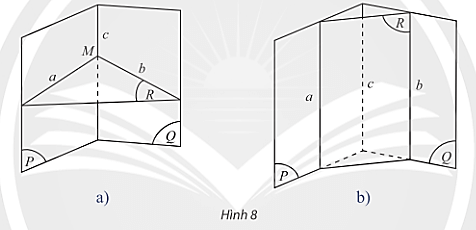
b) Cho ba mặt phẳng \(\left( P \right),\left( Q \right),\left( R \right)\) cắt nhau theo ba giao tuyến \(a,b,c\) phân biệt với \(a = \left( P \right) \cap \left( R \right);b = \left( Q \right) \cap \left( R \right);c = \left( P \right) \cap \left( Q \right)\) (Hình 8).
Nếu \(a\) và \(b\) có điểm chung \(M\) thì điểm \(M\) có thuộc \(c\) không?
Hướng dẫn giải chi tiết Hoạt động khám phá 2
Phương pháp giải:
Áp dụng tính chất 5: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất chứa tất cả các điểm chung của hai mặt phẳng đó.
Lời giải chi tiết:
a) Theo đề bài ta có: \(d' \subset \left( P \right),d' \subset \left( Q \right)\) nên \(d'\) là giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\).
Lại có: \(d \subset \left( P \right),d \subset \left( Q \right)\) nên \(d\) cũng là giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\).
Theo tính chất thừa nhận 5: hai mặt phẳng phân biệt có một đường thẳng chung duy nhất. Vậy hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) trùng nhau.
b) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}M \in a\\a \subset \left( P \right)\end{array} \right\} \Rightarrow M \in \left( P \right)\\\left. \begin{array}{l}M \in b\\b \subset \left( Q \right)\end{array} \right\} \Rightarrow M \in \left( Q \right)\end{array}\)
Do đó điểm \(M\) nằm trên giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\). Vậy \(M \in c\).
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Thực hành 1 trang 101 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Vận dụng 1 trang 102 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 2 trang 103 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 3 trang 104 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 3 trang 105 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Vận dụng 2 trang 105 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 1 trang 105 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 2 trang 106 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 3 trang 106 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 4 trang 106 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 5 trang 106 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 6 trang 106 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Bài tập 1 trang 117 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 2 trang 117 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 3 trang 117 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 4 trang 117 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST





